前言#

本章重新回顾了数据库中的基本知识，包含ER图、关系模型、SQL、约束关系和事务等，并通过一些例题来进一步理解。

本章基于 “Fundamentals of Database Systems 6/7th” (《数据库系统基础第6/7版》) 和一些常见的数据库面试八股文。笔记内容仅为个人见解，加入了一些可能不正式甚至不正确的个人见解，请勿过分解读，若存在异议，欢迎与我交流。

NOTE
资料：

Fundamentals of Database Systems 6/7th

数据库系统基础第6/7版

下面是例题跳转链接：

Draw a ER diagram
Convert ER diagram to Relational Model
SQL
Relation Algebra to SQL
Functional Dependency
Normalization
Transaction

ER Diagram#

ER图（Entity-Relationship Diagram）是一种用于描述实体和实体之间的关系的图表，常用于数据库设计。ER图通常包含实体（Entity），属性（Attribute），关系（Relationship）。

Definition

实体（Entity）：实体是数据库中的对象，例如用户、图书、订单等。实体集 (Entity Set) 是具有相同属性的实体的集合。

属性（Attribute）：属性是实体的描述，例如用户名、密码、邮箱等。

联系（Relationship）：联系是实体与实体之间的关系，例如用户和订单之间的关系。联系集 (Relationship Set) 是多个实体之间的联系的集合。

在一个最简单的ER图里，实体集使用 矩形框 表示，属性使用 椭圆/圆形 表示，联系集使用菱形表示。下面是一个简单的ER图：

其中，有一些关键的概念：

实体的码 / 键 (Key) 是 能区分每一个实体的属性集合，码一般分为：候选码(Candidate Key) 、主码 (Primary Key) 和外码 (Foreign Key)

Definition

候选码 (Candidate Key)：候选码是能 确定一个实体的属性的集合，通常由一个或多个属性组成。候补码可以重复，但至少有一个属性不能为空。例如对于员工表中，候选码可以是 [EmployeeID, {EmployeeName, EmployeeEmail}] 表示一个员工可以由员工编号EmployeeID 或员工名字和邮箱的组合{EmployeeName, EmployeeEmail} 来唯一确定。

主码 (Primary Key)：主码是从候选码中唯一人为选择的属性，用于唯一标识一个实体集中的每一个元组 (Turple). 一个实体集中只能有一个主码，但可以有多个候选码。在 ER 图中，主码以 下划线 的形式表示。一条联系一定由实体的主码唯一确定，与联系的属性无关。

外码 (Foreign Key)：当一个是实体集中没有足够的属性去唯一标识一个实体，即它需要由其他的实体集中的属性的组合来唯一标识一个实体。外码通常用于表示关系。例如：大学课程信息保存在实体集 Course 中，它拥有属性 CourseID、CourseName、CourseCredits等。教授信息存在实体集 Professor 中，它拥有属性 ProfessorID、ProfessorName、ProfessorEmail等。学校规定，一节课由课程编号和教师编号唯一确定：{CourseID, ProfessorID}。那么，对于实体集 Course 而言，{CourseID, ProfessorID} 是它的主码，ProfessorID 是外码。

联系集约束 (Constraint): 实体参与联系时需要满足的一些条件，表示实体与联系的关系。

关系类型的度 (Degree) 是指参与该联系集的实体数量。

当 Degree = 1 时，参与联系集的实体只有一个，称为 自反关系 (Recursive Relationship)。例如，员工中，下级需要向上级汇报，于是 Employee 存在自反关系 Report to，有两条线 (关系) 连接 Employee，因为上下级均为员工。
当 Degree = 2 时，此时的联系集称为 二元关系 (Binary Relationship)。

对于最常见的二元关系而言，基数比 (cardinality ratio) 指定了一个实体可以参与的关系实例的最大数量。对于实体集 A 和 B，a 和 b 表示 A 中的一个实体和 B 中的一个实体。可能的基数比如下：

1:1 (One-to-One)：表示 A 中的实体与 B 中的实体一一对应。例如：一个管理者最多只能管理一个部门，一个部门最多只能有一位管理者。
1:N (One-to-Many)：表示 B 中的实体至多与 A 中的一个实体关联。例如：一个孩子 (b) 最多有一个母亲 (a)，而一个母亲 (a) 可以有多个孩子 (b)。
N:1 (Many-to-One)：表示 A 中的实体至多与 B 中的一个实体关联。例如：一个员工 (a) 只能属于一个部门 (b)，一个部门 (b) 可以有多个员工 (a)。
M:N (Many-to-Many)：表示 A 中的实体可以对应0个或多个 B 中的实体关联，反之亦然。例如：一个员工 (a) 可以参与多个项目 (b)，一个项目 (b) 也可以有多个员工 (a) 参与。

我们把二元关系的基数比又称为 码约束 (Key Constraint)。

此外，参与约束 (Participation Constraint) 指定了每个实体可以参与关系实例的 最小数量。如果实体集 A 中每一个实体 a 都参与联系集 R 的实例，则称 A 参与 R 为 完全参与 (Total Participate)。例如：所有的学生 Student 都有选课 Course，则 Student 完全参与 Course。

完全参与在 ER 图中一般以双线标记。

弱实体集 (Weak Entity Set): 没有足够的属性以形成主码的实体集，称为弱实体集。在 ER 图中以用 双线矩形框和双线菱形框 来标记弱实体集及其标识关系。

例如：员工的保险 Dependent 需要依赖员工 Employee 的 EmployeeID 和保险的DependentID 才能唯一确定一个保险，此时，Dependent 是弱实体集。Dependent 中的所有实体，都依赖对应 Employee 的一个员工，所以 Dependent 参与关系时是完全参与，主码约束为 Employee : Dependent = 1 : N.

此时，弱实体集中的属性 DependentID 为部分码 (Partial Key)，在 ER 图中用 虚下划线 表示。

ER 图总结与例题#

下面的图片总结了 ER 图中的重要元素的图形表示：

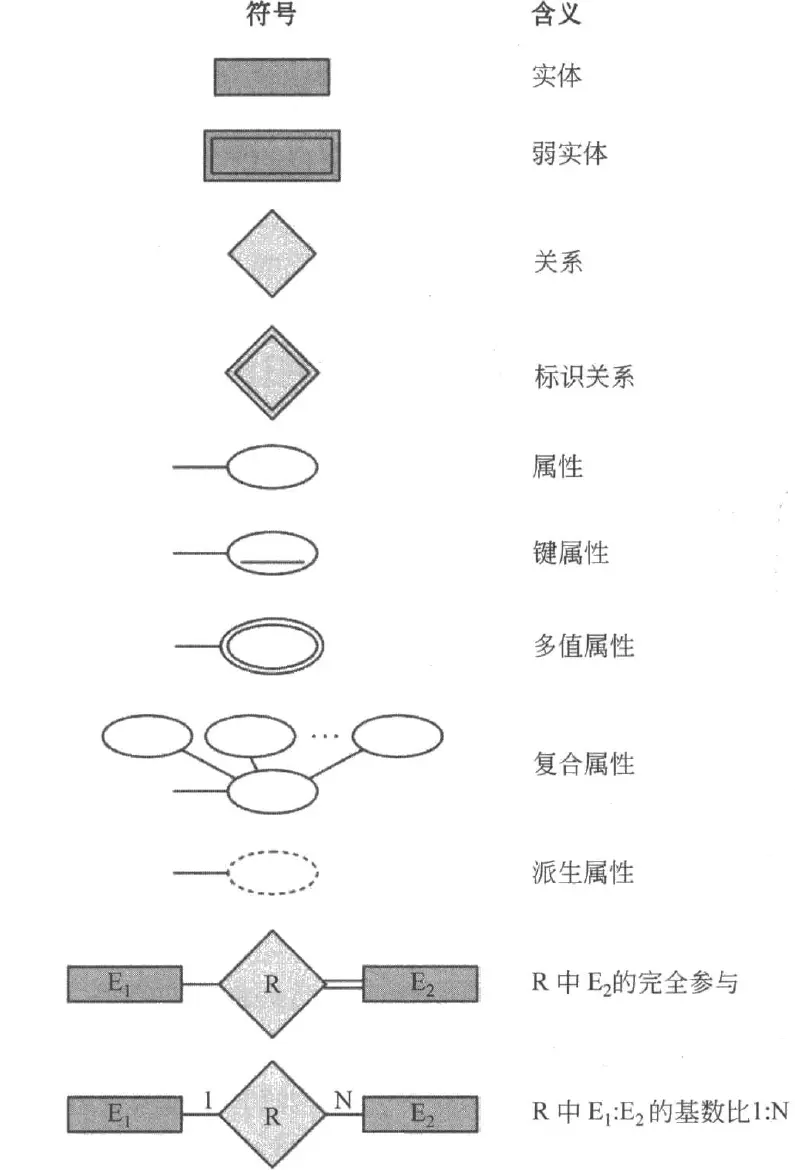
下面是一些设计 ER 图的例子：

我们希望为学校创建一个非常简单的数据库，用于记录教授、学生和课程的相关信息。

每位教授需存储其教员编号、姓名和办公室编号。

每位学生需存储其学号和姓名。

每门课程需存储其课程编号（例如 CS240）和名称。

每门课程仅由一位教授授课。

每位学生必须至少选修一门课程。

需为学生选修的每门课程存储成绩。

要求：每门课程仅设一次授课，且数据库仅包含一个学期数据。

可以明显看到，实体为：教授 Professor (PID, PName, OfficeID), 学生 Student (SID, SName), 课程 Course (CID, CName)。

因为每门课程都需要一位教授授课，教授和课程之间存在联系 taught by，并且 Professor:Course = N:1，且 Course 完全参与 taught by。
学生需要至少选修一门课程，学生和课程之间存在联系 takes，并且 Student:Course = 1:N，且 Student 完全参与 takes。因为每门课程仅设一次授课，因此 Course 完全参与 takes。
成绩是对应每位学生和课程的，因此可以将成绩 Grade 作为联系 takes 的属性。

所以 ER 图如下：

这一题还是比较简单的，基本是最基础的 ER 图转换。下面是一个稍微复杂点的例子：

我们需要设计一个关系数据库，用于存储某大型企业内部培训项目的信息。根据以下描述设计实体关系图：

数据库存储公司每位员工的信息。每位员工拥有姓名和唯一的员工编号。

培训项目中的每门课程都有唯一的课程编号和名称。

课程由公司员工授课并参与学习。

同一课程可多次开设，每次开设具有唯一的开设编号（在该课程内唯一）、具体日期和时间。

每次开设仅由一名员工授课。

数据库存储参与课程学习的员工成绩。

我们同样可以看出实体：Employee (EmpNo, Name), Course (CourseNo, Name)。考虑到开设课程需要记录开设编号、具体日期和时间，因此可以创建一个实体 Offering。考虑到它的属性，包含开设编号、具体日期和时间。但是因为题目说明开设需要和课程相关，所以可以判定开设会被 CourseNo 和 OfferingNo 唯一确定一条记录，所以 Offering 是一个弱实体集。

因为每次开设都由一名员工授课，说明 Offering 完全参与 Teaches，并且 Offering:Employee = N:1。此时我们在设计 Offering 表时，需要加入一个外码 EmpNo 作为外码约束。

员工需要学习课程，但没有说明参与的约束情况，所以存在一个联系集 Enrolled，Employee:Course = M:N。员工成绩需要记录，并且与学习的课程有关，所以成绩 Grade 属性被加入 Enrolled 中。

综合来看，ER 图如下：

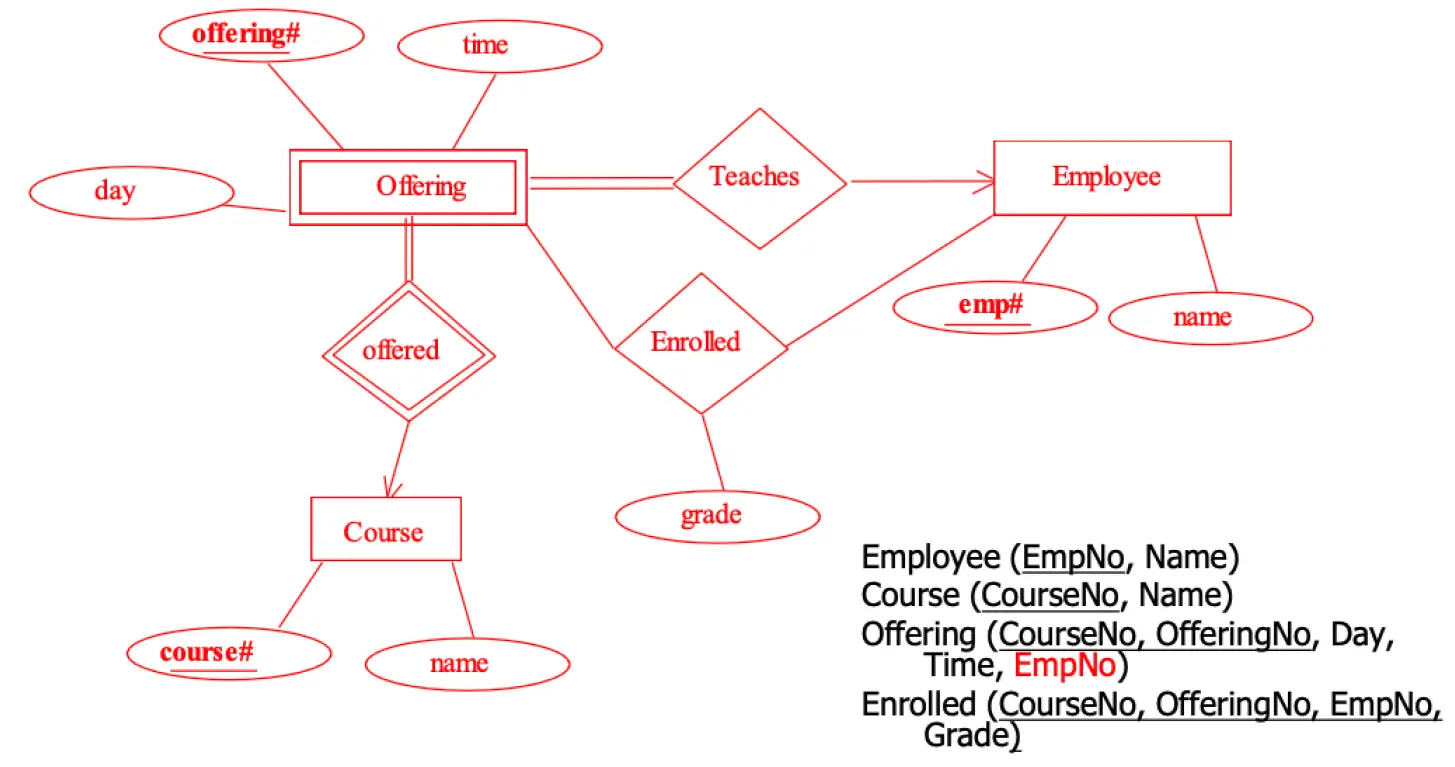
至于为什么在 Offering 表中存在一个外码 EmpNo，因为这遵循了关系模型的外码约束，在下一章复习会说明。

关系模型#

关系 (Relation) 是用于描述数据的主要结构，关系由 关系模式 (Relation Schema) 和 关系实例 (Relation Instance) 组成。关系模式描述了关系中的属性，关系实例描述了关系中的数据，一般以表格形式展示。例如：Student (SID, SName, SDept, SGPA) 是一个关系模式，Student (1, John, CS, 3.5) 是一个关系实例。

对于关系实例，它可以看成是一行行元组 (Tuple) 的集合，一个元组是一个记录 (Record)，记录由 属性值 (Attribute Value) 组成。

对于关系模型而言，其最重要的是它的 完整性约束 (Integrity Constraint)，用于保证关系实例的完整性。这些约束源于数据库所表示的微观世界中的规则。。

下面是几种最常见的关系模型完整性约束：

域约束 (Domain Constraint): 属性值受到其值域的限制，属性值必须在给定的值域内。例如：定义 SID 属性，它的值域为 [1, 100]，那么Student (1, John, CS, 3.5) 是一个有效的关系实例，而 Student (101, John, CS, 3.5) 是一个无效的关系实例。
主码约束 (Primary Key Constraint): 一个关系实例必须具有 唯一非空 的主码，主码是关系实例的标识符。例如：定义 Student (SID, SName, SDept, SGPA)，其中 SID 是主码，SID 对于所有的记录而言必须是唯一的，不能为空。
外码约束 (Foreign Key Constraint): 外码用于维护表与表之间的关系。它确保在一个表中的值必须在另一个表中存在，从而保持数据的一致性。外码通常用于实现一对多（One-to-Many）或多对多（Many-to-Many）的关系。之后会有详细的例子说明。
参照完整性约束 (Referential Integrity Constraint): 引用完整性约束用于确保数据在表中的引用关系是正确的。例如，如果一个表中的某个字段引用了另一个表中的主码字段，那么该字段的值必须在另一个表中存在，并且取值一致。

根据这些约束规则，我们可以将 ER 图转换为关系模型，下面是转换的规则：

转换实体集：每个实体集对应一个关系表，关系表的模式就是实体集的属性名称。
- 强实体集转换：先创建一个包含所有属性的关系模式，再标记主码。
- 弱实体集转换：先创建一个包含所有属性的关系模式，再 添加依赖的实体集的主码作为外码，与弱实体集的部分码合并做主码。例如：Project 有两个属性 proj_id 和 date，proj_id 是部分码。Project 依赖于 Department，于是添加 Department 的主码 dept_id 为外码，联合部分码 proj_id 一起为主码，即Project 的主码为 {proj_id, dept_id}。
转换联系集：
- 1:1 关系: 将 非完全参与 的实体集的主码作为外码 插入到完全参与的实体集中。例如：一个部门只能且一定有一位员工管理，一位员工只能最多管理一个部门。Employee 的主码为 emp_id，Department 的主码为 dept_id。此时，Department 是完全参与，所以将emp_id作为外码插入到Department中。Department的属性为 dept_id, emp_id, ...，主码还是 dept_id。
  当然，如果双方实体都是部分参与，则可以采用 在任意一方加入另一方的主码作为外码，或者为它们的联系集 设计一个独立表，包含双方的主码作为外码，主码任意其中一个即可。
- 1:N 关系: 在 N 的一侧的实体集中加入另一个实体集的主码作为外码。例如：一个员工只能属于一个部门，一个部门可以有多个员工。此时，外码约束的存在确保了部门 Department 中的所有员工都存在 Employee，即每一位员工都对应一个部门，此时部门的主码 dept_id 作为外码插入到 Employee 中。注意：反过来将 emp_id 作为外码存在 Department 表里是错误的，如果在 Department 放外码，一个部门就只能关联一个员工，违背了1:N的语义。
- M:N 关系: 在多对多的关系中，通常的做法是 创建独立的关系表，包含双方主码作为外码，主码是外码的组合。例如：员工可以选择任意课程，课程可以包含任意员工。这种情况下需要创建中间表 Takes，包含emp_id和course_id两个外码，并且它们联合为主码，即 Takes 的主码为 {emp_id, course_id}。

有了这些规则之后，我们就可以将 ER 图转换为关系模型了。

关系模型例题#

下面是一些转换 ER 图的例子：

请将下面的 ER 图转换成关系模型。

根据转换规则，我们先转换实体集：

强实体集有：BUS, ROUTE, DRIVER.

BUS (licence, capacity)
ROUTE (number, departure station, destination station)
DRIVER (id, name, phone)

SCHEDULE 是弱实体集，它完全参与 ROUTE 的关系，所以将 ROUTE 的主码 number 作为外码插入到 SCHEDULE 中，并且与部分码 departure time 合并做主码，于是有：

SCHEDULE (number, departure time)

接下来我们来转换联系集。我们发现 BUS 与 SCHEDULE 之间存在 M:N 的关系，DRIVER 与 SCHEDULE 也存在 M:N 的关系。所以这两个联系集都需要创建中间表：

DRIVES (id, number, departure-time)
BUS-IN-USE (license, number, departure-time)

下面是一题稍微复杂的实际性问题：

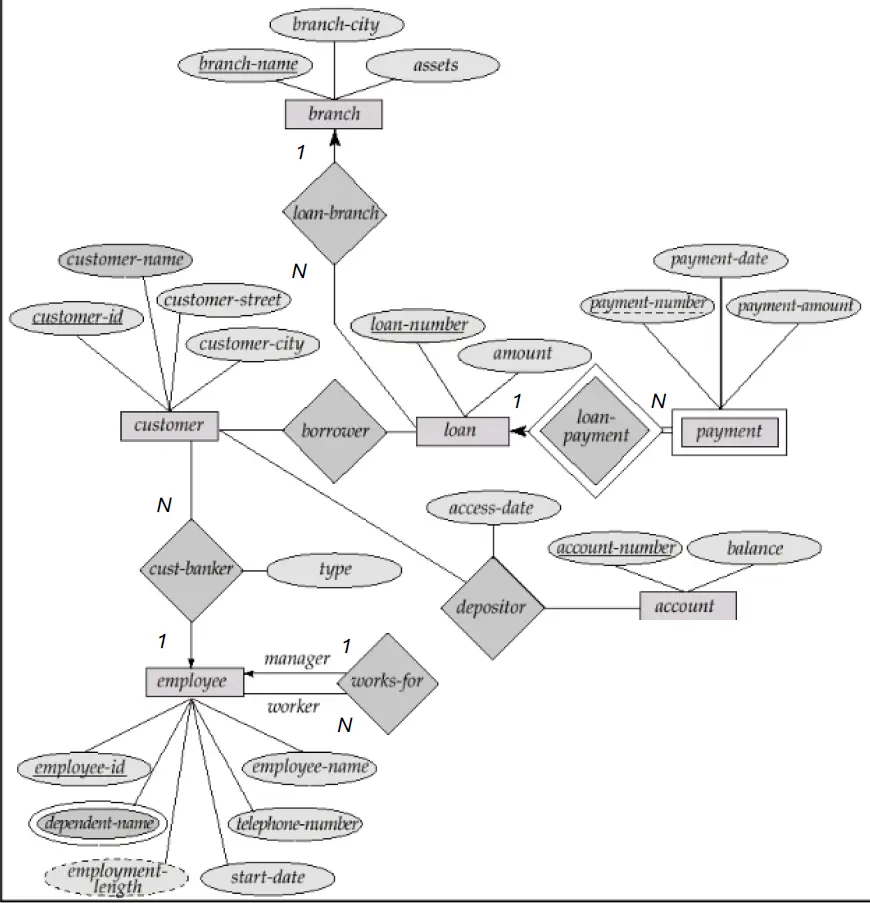
请将下面的 ER 图转换成关系模型。

同样的，根据转换规则，我们先转换实体集：

强实体集有：branch, customer, loan, employee, account (忽略了多值属性)

branch (branch-name, assets, branch-city)
customer (customer-id, customer-name, customer-city, customer-street)
loan (loan-number, amount)
employee (employee-id, employee-name, dependent-name, telephone-number, employment-length, start-date)
account (account-number, balance)

弱实体集有: payment，它完全参与 loan 的关系 loan-payment，所以将 loan 的主码作为外码添加到 payment 中，并与部分码 payment-number 形成主码。

payment (payment-number, loan-number, payment-amount, payment-date)

接下来转换联系集：

对于 1:N 的关系:

对于自反关系 works-for，将 1 侧的主码作为外码添加到 N 侧。此时两侧是一样的，所以会进行一些重命名。修改后的 employee ：employee (employee-id, employee-name, dependent-name, telephone-number, employment-length, start-date, manager-id)
关系 cust-banker 重复同样的操作，可以得到：customer (customer-id, customer-name, customer-city, customer-street, employee-id, type) 注意联系集的属性也需要添加。
关系 loan-branch 重复同样的操作，可以得到：loan (loan-number, amount, branch-id)

对于 M:N 的关系：

关系 depositor 提取出两侧的主码作为外码，并合并做主码，可以得到：deposit (customer-id, account-number, access-date)
关系 borrower 提取出两侧的主码作为外码，并合并做主码，可以得到：borrower (loan-number, customer-id)

所以最后我们得到了如下的关系模型：

branch (branch-name, assets, branch-city)
customer (customer-id, customer-name, customer-city, customer-street, employee-id, type)
loan (loan-number, amount, branch-id)
employee (employee-id, employee-name, dependent-name, telephone-number, employment-length, start-date, manager-id)
account (account-number, balance)
payment (payment-number, loan-number, payment-amount, payment-date)
deposit (customer-id, account-number, access-date)
borrower (loan-number, customer-id)

SQL#

SQL (Structured Query Language) 是一种用于管理关系数据库的语言。SQL由数据操作语言 DML (Data Manipulation Language)、数据定义语言 DDL (Data Definition Language)、数据控制语言 DCL (Data Control Language) 组成。

下面是一些 SQL 的基本语法：

增删改和约束#

创建表：

1
CREATE TABLE [IF NOT EXISTS] <table_name> (
2
  <field_name> <data_structure>,
3
    ...
4
);

删除表：

1
DROP TABLE [IF EXISTS] <table_name>;

插入:

1
-- Insert with all values
2
INSERT INTO <table_name>
3
VALUES (field1, field2, ...);
4

5
-- Insert with partial values
6
INSERT INTO <table_name> (col1, col2, ...)
7
VALUES (field1, field2, ...);

修改数据：

1
UPDATE <table_name>
2
SET field1 = value1, field2 = value2,...
3
WHERE <condition>;

删除数据：

1
-- Delete with condition
2
DELETE FROM <table_name> WHERE <condition>;
3

4
-- Delete all records
5
DELETE FROM <table_name>;

约束

1
-- Primary KEY
2
CREATE TABLE [IF NOT EXISTS] <table_name> (
3
  field_name data_structure PRIMARY KEY,
4
    ...
5
);
6

7
-- Foreign KEY
8
CREATE TABLE [IF NOT EXISTS] <table_name> (
9
  PersonID int,
10
    FOREIGN KEY (PersonID) REFERENCES Persons(PersonID),
11
    ...
12
);
13

14
-- NOT NULL
15
CREATE TABLE [IF NOT EXISTS] <table_name> (
16
  field_name data_structure PRIMARY KEY NOT NULL,
17
    ...
18
);
19

20
-- Unique
21
CREATE TABLE [IF NOT EXISTS] <table_name> (
22
  field_name data_structure UNIQUE,
23
    ...
24
);
25

26
-- Default Value
27
CREATE TABLE [IF NOT EXISTS] <table_name> (
28
  field_name data_structure DEFAULT XXX,
29
    ...
30
);

查询语句及其语法#

查询语句的使用频率最高，下面详细介绍了查询语句中的部分：

SELECT 的语句顺序为：

1
SELECT [DISTINCT] <attributes_list>  -- DISTINCT: 去重
2
FROM <table_list>                    -- FROM: 表的集合，可以多个表，可以使用 AS 重命名
3
[WHERE <condition>]                  -- WHERE: 条件
4
[GROUP BY <group_attributes_list>]   -- GROUP BY: 将group_attributes 相同的记录分组放在一起
5
[HAVING <group_condition>]           -- HAVING: 对GROUP BY 之后的分组进行条件筛选
6
[ORDER BY <order_attributes_list>]   -- ORDER BY: 排序 SELECT 之后的结果表格

重命名、字符匹配和排序#

重命名：可以使用 AS 对 attributes_list 或 table_list 进行重命名。在语句中 AS 可以省略。

1
SELECT <attributes_list> [AS] <attributes_alias>
2
FROM <table_list> [AS] <table_alias>
3
WHERE <condition>;

字符匹配：可以通过 LIKE 语句匹配字符，进行模糊查询。可以通过 % 匹配任意字符，通过 _ 匹配任意一个字符。

1
SELECT <attributes_list>
2
FROM <table_list>
3
WHERE <condition> LIKE <pattern>;

例如：找到所有学生中名字包含 “JONES” 的学生。

1
SELECT *
2
FROM student
3
WHERE name LIKE '%JONES%';

排序：可以使用 ORDER BY 对查询后的结果进行排序。

升序 (默认)：ASC
降序：DESC

1
SELECT <attributes_list>
2
FROM <table_list>
3
ORDER BY <order_attributes_list>;

集合运算和空检测#

集合运算：在 SQL 中可以使用集合运算符对关系进行运算，例如交 $\cup$ INTERSECT, 并 $\cap$ UNION , 减 $-$ EXCEPT。

下面是几个集合运算的例子：

对于如下关系模式，* 表示主码：

1
Sailor (sid*, sname, rating, age);
2
Boat (bid*, bname, color);
3
Reservation (sid*, bid*, day*);

找到被预留的红船或绿船的 bid

1
SELECT B.bid
2
FROM reservation AS R, boat AS B
3
WHERE B.bid = R.bid AND (B.color = 'red' OR B.color = 'green');
4

5
-- 等价于两个查询的结果的并集
6
SELECT B.bid
7
FROM reservation AS R, boat AS B
8
WHERE B.bid = R.bid AND B.color = 'red';
9
UNION
10
SELECT B.bid
11
FROM reservation AS R, boat AS B
12
WHERE B.bid = R.bid AND B.color = 'green';

找到预留所有船的船员名字。那么可以翻译为，不存在没有被预订的船，我们可以先查询所有的船，再使用 EXCEPT 减去所有有预订的船就行。

1
SELECT S.sname
2
FROM sailor AS S
3
WHERE NOT EXISTS (        -- 找到所有的船
4
  SELECT B.bid
5
  FROM Boat AS B
6
) EXCEPT (                -- 减去所有有预订的船
7
  SELECT R.bid
8
  FROM reservation AS R
9
  WHERE R.sid = B.sid
10
)

空 / 数量检测：可以通过 EXISTS, NOT EXISTS, IS NULL 和 NOT NULL 检测一个关系是否为空。还可以通过 ANY, SOME, ALL 语句检测一个关系是否满足某个条件。

聚合函数#

聚合函数：可以通过 COUNT, SUM, AVG, MAX, MIN 函数对关系进行聚合，并且计算一个结果。

COUNT ([DISTINCT] <attributes_list>): 计算关系中 attributes_list 的数量。
SUM ([DISTINCT] <attributes_list>): 计算关系中 attributes_list 的和。
AVG ([DISTINCT] <attributes_list>): 计算关系中 attributes_list 的平均值。AVG 会自动忽略NULL值。
MAX (<attributes_list>): 计算关系中 attributes_list 的最大值。
MIN (<attributes_list>): 计算关系中 attributes_list 的最小值。

例如：找到最老的船员的名字与年龄。

1
SELECT S.sname, S.age
2
FROM sailor AS S
3
WHERE S.age = (
4
  SELECT MAX(S1.age)
5
  FROM sailor AS S1
6
)

这里使用了嵌套查询，因为除了使用分组外，SELECT 的字句中若要使用聚合函数，则不能存在任何非聚合函数的属性列。

例如一个错误示例：

1
SELECT S.Sname, MAX(S.age)   -- ❌聚合函数不能与非聚合函数的属性列一起使用
2
FROM sailor AS S

分组查询#

分组：通过 GROUP BY 对关系进行分组，可以找到同样属性值的记录。HAVING 用于对分组后的结果进行筛选。

我们通过一些例子来理解：

找出每个等级中 年龄至少为18岁 的最年轻水手，每个等级至少需有两名符合 此条件 的水手。(Find the age of the youngest sailor with age > 18, for each rating with at least 2 such sailors)

1
SELECT S.rating, MIN(S.age) AS min_age  -- 仅在GROUP BY存在时才允许聚合函数与其他属性列一起使用
2
FROM sailor AS S
3
WHERE S.age > 18                        -- 先找到所有大于18岁的
4
GROUP BY S.rating                       -- 通过等级进行分组
5
HAVING COUNT(S.sid) >= 2                -- 再筛选出等级至少两位的

找到每一个红船被预订的数量。可以转换为：找到所有被预订的红船，再通过 GROUP BY 进行分组计算其数量。

1
SELECT B.bid, COUNT(R.sid) AS RESERVATION_COUNT
2
FROM reservation AS R, boat AS B
3
WHERE B.bid = R.bid AND B.color = 'red'    -- 找到所有被预订的红船
4
GROUP BY B.bid                             -- 通过bid进行分组

注意，这里不能先找到所有预订的船，再在 HAVING 处再筛选红船，因为只有在 GROUP BY 后形成的属性列的属性才能进行 HAVING 筛选。

1
SELECT B.bid, COUNT(R.sid) AS RESERVATION_COUNT
2
FROM reservation AS R, boat AS B
3
WHERE B.bid = R.bid
4
GROUP BY B.bid
5
HAVING B.color = 'red'    -- ❌ B.color不是分组之后形成的属性列，不能进行HAVING筛选

找到所有等级船员中平均年龄最小的等级。可以转换为：将船员按照等级进行分组，计算每个分组的平均年龄，再找到最小的等级。

1
SELECT T.rating, T.avg_age
2
FROM (                     -- 从分组好的表中进一步查找条件
3
  SELECT S.rating, AVG(S.age) AS avg_age
4
  FROM sailor AS S
5
  GROUP BY S.rating
6
) AS T
7
WHERE T.avg_age = (        -- 找到年龄最小的
8
  SELECT MIN(T1.avg_age)
9
  FROM T
10
);

注意：聚合函数不能自身嵌套，下面是错误示例：

1
SELECT S.rating
2
FROM sailor AS S
3
WHERE S.age = (
4
  SELECT MIN(AVG(S1.age))   -- ❌聚合函数不能自身嵌套
5
  FROM sailor AS S1
6
  GROUP BY S1.rating
7
)

连接#

连接 (Join)：连接可以查询两个表中的相同字段的记录。连接分为：内连接 (Inner Join)，外连接 (Outer Join)，自然连接 (Natural Join)。

内连接 (Inner Join)：用于查询两个表之间相同字段的记录，只返回两表中”有匹配”的记录。一般通过 INNER JOIN ... ON 语句启用，或 WHERE 中进行连接。INNER JOIN ... ON 可以省略。
外连接 (Outer Join)：用于查询两个表之间相同字段的记录，并且包含其他信息。它又可以分为左外连接 (Left Outer Join)，右外连接 (Right Outer Join)，全外连接 (Full Outer Join)。
自然连接 (Natural Join)：自动识别同名列进行等值连接，且结果中同名列只出现一次。它与内连接 (Inner Join) 类似，但是它不包含 ON 子句。

下面是三种连接的例子：

若有如下表格：

Student:

1
SID  | SName  | DeptID
2
-----+--------+--------
3
001  | Alice  | 10
4
002  | Bob    | 20
5
003  | Carol  | 30
6
004  | David  | NULL

Departments:

1
DeptID | DeptName
2
-------+------------------
3
10     | Computer Science
4
20     | Mathematics
5
40     | Physics

我们执行内连接：

1
SELECT Students.SID, Students.SName, Departments.DeptName
2
FROM Students
3
INNER JOIN Departments ON Students.DeptID = Departments.DeptID;
4

5
-- 隐式写法
6
SELECT Students.SID, Students.SName, Departments.DeptName
7
FROM Students, Departments
8
WHERE Students.DeptID = Departments.DeptID;

执行的结果是：

1
SID  | SName  | DeptName
2
-----+--------+------------------
3
001  | Alice  | Computer Science
4
002  | Bob    | Mathematics

内连接只包含匹配的记录。而外连接分为左外连接 (Left Outer Join)，右外连接 (Right Outer Join)，全外连接 (Full Outer Join)。其区别就是在匹配的记录的基础上，再添加左表/右表/两表非匹配的记录。

1
SELECT Students.SID, Students.SName, Departments.DeptName
2
FROM Students
3
LEFT JOIN Departments ON Students.DeptID = Departments.DeptID;

这是一个左外连接，它 保留左表所有记录，右表无匹配时填 NULL，结果为：

1
SID  | SName  | DeptName
2
-----+--------+------------------
3
001  | Alice  | Computer Science
4
002  | Bob    | Mathematics
5
003  | Carol  | NULL              ← 保留了Carol
6
004  | David  | NULL              ← 保留了David

同理，右外连接保留右表所有记录，左表无匹配时填 NULL：

1
SELECT Students.SID, Students.SName, Departments.DeptName
2
FROM Students
3
RIGHT JOIN Departments ON Students.DeptID = Departments.DeptID;

结果为：

1
SID  | SName  | DeptName
2
-----+--------+------------------
3
001  | Alice  | Computer Science
4
002  | Bob    | Mathematics
5
NULL | NULL   | Physics           ← 保留了Physics

全外连接 (FULL OUTER JOIN) 保留两表所有记录，无匹配的都用 NULL 填充。两张表的所有记录都出现，它是 LEFT JOIN + RIGHT JOIN 的并集。

1
SELECT Students.SID, Students.SName, Departments.DeptName
2
FROM Students
3
FULL OUTER JOIN Departments ON Students.DeptID = Departments.DeptID;

结果为：

1
SID  | SName  | DeptName
2
-----+--------+------------------
3
001  | Alice  | Computer Science
4
002  | Bob    | Mathematics
5
003  | Carol  | NULL              ← 左表未匹配
6
004  | David  | NULL              ← 左表未匹配
7
NULL | NULL   | Physics           ← 右表未匹配

对于自然连接 (Natural Join)，它与内连接 (Inner Join) 类似，它自动 识别同名列进行等值连接，且结果中同名列只出现一次 (正常内连接中同名列会重复)。

1
SELECT *
2
FROM Students
3
NATURAL JOIN Departments;

结果是：

1
DeptID | SID  | SName  | DeptName
2
-------+------+--------+------------------
3
10     | 001  | Alice  | Computer Science
4
20     | 002  | Bob    | Mathematics

下面是三种连接对比总结表：

连接类型	返回记录	匹配条件	未匹配处理	使用场景
INNER JOIN	两表都匹配的	必须显式指定	丢弃	只需要完全匹配数据
LEFT JOIN	左表全部 + 匹配的右表	必须显式指定	右表填NULL	主表数据必须全部显示
RIGHT JOIN	右表全部 + 匹配的左表	必须显式指定	左表填NULL	（较少用，可用LEFT替代）
FULL JOIN	两表全部记录	必须显式指定	双方填NULL	需要完整数据集合
NATURAL JOIN	两表匹配的（内连接）	自动识别同名列	丢弃	表设计规范且字段明确

视图 (View): 视图是从其他表格中派生出的虚拟表，只允许有限的操作，以方便表示某些操作，保护数据安全。

视图创建语法，相当于在查询语句外部添加了一个新表格创建：

1
CREATE VIEW view_name AS
2
  SELECT <attributes_list>
3
  FROM <table_name>
4
  WHERE <condition>;

若视图不再需要，则可以直接删除它：

1
DROP VIEW view_name;

如果需要更新视图中的数据，并使其修改能映射到基本的表格中，则需要使用 UPDATE 语句：

1
UPDATE view_name
2
SET <attribute_name> = <new_value>
3
WHERE <condition>;

SQL 经典例题#

以上是 SQL 的基础语法，下面我们根据一些例题来加深理解。

逻辑问题#

对于如下关系模式，* 表示主码：
1
Sailor (sid*, sname, rating, age);
2
Boat (bid*, bname, color);
3
Reservation (sid*, bid*, date*);
Find sid’s of sailors who’ve reserved a red or a green boat
找到所有预订了红色或绿色船的船员的sid

对于题目1，其中的关键词 or 表示：只要预订过至少一艘红色或绿色船即可，bid 需要出现在 Reservation 表中，并且bid 对应的 color 需要是红色或绿色。

我们可以使用内连接，它只保留了匹配的记录：

1
SELECT DISTINCT R.sid
2
FROM Reservation R
3
JOIN Boat B ON R.bid = B.bid
4
WHERE B.color = 'red' OR B.color = 'green';
5

6
-- 或隐式写法
7
SELECT DISTINCT R.sid
8
FROM Reservation R, Boat B
9
WHERE R.bid = B.bid AND (B.color = 'red' OR B.color = 'green');

当前，我们还可以拆分为两个查询：先找到预订了这些船的所有船员，再找出红色或绿色的船。

1
SELECT DISTINCT R.sid
2
FROM Reservation R
3
WHERE R.bid IN (
4
    SELECT B.bid
5
    FROM Boat B
6
    WHERE B.color = 'red' OR B.color = 'green'
7
);

此外，还可以采用集合的思想，将两个查询的结果集进行并集：

1
SELECT DISTINCT R.sid
2
FROM Reservation R, Boat B
3
WHERE R.bid = B.bid AND B.color = 'red'
4

5
UNION
6

7
SELECT DISTINCT R.sid
8
FROM Reservation R, Boat B
9
WHERE R.bid = B.bid AND B.color = 'green';

Find sid’s of sailors who’ve reserved a red and a green boat
找到所有预订了红色和绿色船的船员的sid

对于题目2，它与题目1的要求相似，只是要求预订了红色和绿色船。但是我们不能直接将 OR 改为 AND，因为 一艘船不可能同时是红色和绿色，WHERE 的条件是对 同一行记录的约束。

1
-- ❌ 错误！这会返回空集
2
SELECT DISTINCT R.sid
3
FROM Reservation R
4
JOIN Boat B ON R.bid = B.bid
5
WHERE B.color = 'red' AND B.color = 'green';

正确的解法是使用自连接 (Self-Join)，即拓展一下连接表格，添加 color 为重复的列，分别匹配 red 和 green。

1
SELECT DISTINCT R1.sid
2
FROM Reservation R1
3
JOIN Boat B1 ON R1.bid = B1.bid
4
JOIN Reservation R2 ON R1.sid = R2.sid
5
JOIN Boat B2 ON R2.bid = B2.bid
6
WHERE B1.color = 'red' AND B2.color = 'green';

R1找红色船的预订，R2找绿色船的预订，通过 R1.sid = R2.sid 找到同时满足两个条件的船员

当然这么写太复杂了，一般情况下我们会使用两次 EXISTS 来解决：

1
SELECT DISTINCT S.sid
2
FROM Sailor S
3
WHERE EXISTS (  -- 找到预订了红色船的船员
4
    SELECT *
5
    FROM Reservation R1, Boat B1
6
    WHERE R1.sid = S.sid
7
      AND R1.bid = B1.bid
8
      AND B1.color = 'red'
9
)
10
AND
11
EXISTS (       -- 找到预订了绿色船的船员
12
    SELECT *
13
    FROM Reservation R2, Boat B2
14
    WHERE R2.sid = S.sid
15
      AND R2.bid = B2.bid
16
      AND B2.color = 'green'
17
);

这是最清楚的解法，分步完成。当然，我们也可以将其改为交集的形式：

1
SELECT DISTINCT R.sid
2
FROM Reservation R, Boat B
3
WHERE R.bid = B.bid AND B.color = 'red'
4

5
INTERSECT
6

7
SELECT DISTINCT R.sid
8
FROM Reservation R, Boat B
9
WHERE R.bid = B.bid AND B.color = 'green';

Find sid’s of sailors who’ve reserved a red boat BUT NOT a green boat
找到预订了红色船 但没有 预订绿色船的船员

题目3意味着：必须预订至少一艘红色船，但从未预订绿色船。我需要找到的是集合：{红色船船员} - {绿色船船员}

我们可以使用 NOT EXISTS 或 NOT IN，用于排除绿船船员：

1
SELECT DISTINCT R.sid
2
FROM Reservation R
3
JOIN Boat B ON R.bid = B.bid
4
WHERE B.color = 'red'        -- 外层找预订了红色船的船员
5
  AND NOT EXISTS (           -- NOT EXISTS 排除那些预订了绿色船的船员
6
      SELECT *
7
      FROM Reservation R2
8
      JOIN Boat B2 ON R2.bid = B2.bid
9
      WHERE R2.sid = R.sid   -- 注意：嵌套的地方需要满足上层查询的条件
10
        AND B2.color = 'green'
11
  );

当前，运用集合减的知识也可以清楚解决：

1
SELECT DISTINCT R.sid
2
FROM Reservation R, Boat B
3
WHERE R.bid = B.bid AND B.color = 'red'
4

5
EXCEPT
6

7
SELECT DISTINCT R.sid
8
FROM Reservation R, Boat B
9
WHERE R.bid = B.bid AND B.color = 'green';

Find sid’s of sailors who’ve reserved EVERY red boat.
找到预订了所有红色船的船员

题目4要求找到一个船员，他预订了所有的红色船。这意味着 不存在一艘红色船是该船员没有预订的。

所以根据这个逻辑，运用 NOT EXISTS 或集合减 EXCEPT 可以得到：

1
SELECT S.sid
2
FROM Sailor S
3
WHERE NOT EXISTS (        -- 所有红色船的记录
4
    SELECT B.bid
5
    FROM Boat B
6
    WHERE B.color = 'red'
7
      AND NOT EXISTS (    -- 船员预订的记录
8
          SELECT *
9
          FROM Reservation R
10
          WHERE R.sid = S.sid
11
            AND R.bid = B.bid
12
      )
13
);

Find sid’s of sailors who’ve reserved ONLY red boats
找到只预订了红色船的船员（不能预订其他颜色）

翻译一下题目5就是：一个船员至少预订了一艘船，且不存在颜色不是红色的船。

充分运用集合的方法：

1
SELECT S.sid
2
FROM Sailor S
3
WHERE EXISTS (      -- 至少预订了一艘船
4
    SELECT *
5
    FROM Reservation R
6
    WHERE R.sid = S.sid
7
)
8
AND NOT EXISTS (    -- 不存在预订非红色船的记录
9
    SELECT *
10
    FROM Reservation R
11
    JOIN Boat B ON R.bid = B.bid
12
    WHERE R.sid = S.sid
13
      AND B.color <> 'red'
14
);

Find sid’s of sailors whose rating is greater than SOME sailor named ‘Bob’
找到rating大于某个名叫Bob的船员的所有船员

题目6是一个存在量词的题目，我们可以使用 ANY 或 SOME 去解决这个逻辑问题，或者使用聚合函数。

1
SELECT S.sid
2
FROM Sailor S
3
WHERE S.rating > ANY (
4
    SELECT S2.rating
5
    FROM Sailor S2
6
    WHERE S2.sname = 'Bob'
7
);
8

9
SELECT S.sid
10
FROM Sailor S
11
WHERE S.rating > (    -- 使用聚合函数
12
    SELECT MIN(S2.rating)
13
    FROM Sailor S2
14
    WHERE S2.sname = 'Bob'
15
);

Find sid’s of sailors whose rating is greater than ALL sailors named ‘Bob’
找到rating大于所有名叫Bob的船员的船员

这题和题目6的差别是，名叫 “Bob” 的船员可能有很多个，我们可以使用 ALL 代替即可。

1
SELECT S.sid
2
FROM Sailor S
3
WHERE S.rating > ALL (
4
    SELECT S2.rating
5
    FROM Sailor S2
6
    WHERE S2.sname = 'Bob'
7
);
8

9
SELECT S.sid
10
FROM Sailor S
11
WHERE S.rating > (    -- 使用聚合函数
12
    SELECT MAX(S2.rating)
13
    FROM Sailor S2
14
    WHERE S2.sname = 'Bob'
15
);

Find sid’s of sailors who’ve reserved a red boat OR a green boat BUT NOT a blue boat.
找到预订了红色或绿色船但没预订蓝色船的船员

题目8是题目1和题目3的复合形式，我们可以组合他们得到结果：

1
SELECT DISTINCT R.sid
2
FROM Reservation R
3
JOIN Boat B ON R.bid = B.bid
4
WHERE (B.color = 'red' OR B.color = 'green')
5
  AND NOT EXISTS (
6
      SELECT *
7
      FROM Reservation R2
8
      JOIN Boat B2 ON R2.bid = B2.bid
9
      WHERE R2.sid = R.sid
10
        AND B2.color = 'blue'
11
  );

当然，可以使用非常显而易见的集合运算代替：

1
SELECT DISTINCT R.sid
2
FROM Reservation R, Boat B
3
WHERE R.bid = B.bid AND B.color = 'red'
4

5
UNION
6

7
SELECT DISTINCT R.sid
8
FROM Reservation R, Boat B
9
WHERE R.bid = B.bid AND B.color = 'green'
10

11
EXCEPT
12

13
SELECT DISTINCT R.sid
14
FROM Reservation R, Boat B
15
WHERE R.bid = B.bid AND B.color = 'blue';

Find sid’s of sailors who’ve reserved EXACTLY two boats
找到恰好预订了两艘船的船员

分析题目9可以发现，它需要我们按照预订船的数量进行分组，然后筛选出预订数为2的船员，使用 GROUP BY 和 HAVING 来解决。

1
SELECT R.sid
2
FROM Reservation R
3
GROUP BY R.sid
4
HAVING COUNT(DISTINCT R.bid) = 2;

Find sid’s of sailors who have the same rating as some sailor named ‘Bob’
找到与某个Bob有相同rating的船员

这一题我们需要先找到 Bob 的 rating，再排除他自己：

1
SELECT S.sid
2
FROM Sailor S
3
WHERE S.rating IN (
4
    SELECT S2.rating
5
    FROM Sailor S2
6
    WHERE S2.sname = 'Bob'
7
)
8
AND S.sname <> 'Bob';  -- 排除Bob自己

逻辑问题总结#

总结一下这些逻辑问题，我们可以知道如下逻辑及其解决方案：

自然语言	SQL实现策略	推荐方法
OR（或）	内连接 / 取并集	直接 `JOIN` + `OR`
AND（且）	自连接 / 多重 `EXISTS` / 取交集	`INTERSECT`
BUT NOT（但不）	多重 `NOT EXISTS` / 取减集	`NOT EXISTS` / `EXCEPT` / `NOT IN`
EVERY（所有）	转换为双重否定 `NOT EXISTS`	`NOT EXISTS` / `EXCEPT` / `NOT IN`
SOME/ANY（某些）	`> ANY (subquery)`	`ANY` / `SOME`
ALL（全部）	转换为双重否定 `NOT EXISTS`	`NOT EXISTS` / `EXCEPT` / `NOT IN`
ONLY（仅）	`NOT EXISTS` 非目标	`NOT EXISTS`
EXACTLY N（恰好N个）	`HAVING COUNT = N`	`GROUP BY` + `HAVING`
AT LEAST N（至少N个）	`HAVING COUNT >= N`	`GROUP BY` + `HAVING`
AT MOST N（最多N个）	`HAVING COUNT <= N`	`GROUP BY` + `HAVING`
MORE THAN / LESS THAN（多于/少于）	子查询比较	`(SELECT X)` 比较 `(SELECT B)`

此外，在写嵌套查询时，我们时常需要匹配上级查询和下级查询的字段，但时常不知道什么时候匹配，什么时候不匹配。

答案是：当且仅当子查询需要”知道” 当前检查的是哪个属性值时，才需要用外层查询的属性值来匹配。

例如：Find the names of sailors who have reserved bid=103

1
SELECT S.sname
2
FROM Sailor S
3
WHERE EXISTS (
4
    SELECT *
5
    FROM Reservation R
6
    WHERE R.bid = 103
7
      AND R.sid = S.sid
8
);

如果没有 R.sid = S.sid，那么只要存在任何人预订了103号船，WHERE 条件就为真，所有船员都会被返回。

当有 R.sid = S.sid 时，针对每个船员单独判断，只返回真正预订了103号船的人。

但是如果我们将 EXISTS 改为 IN，那么子查询只执行一次，且不使用外层查询的值，结果集在外层查询前就确定了，这样的性能更高。且结果正确。

1
SELECT S.sname
2
FROM Sailor S
3
WHERE S.sid IN (
4
    SELECT R.sid
5
    FROM Reservation R
6
    WHERE R.bid = 103
7
);

我们一般将 EXISTS 和 NOT EXISTS 称为相关子查询，而IN 和 NOT IN 称为 非相关子查询。

所以，总结来说什么时候需要显式关联：

查询类型	是否需要显式关联	原因
EXISTS 子查询	✅ 必须	子查询不返回具体值，只返回TRUE/FALSE
NOT EXISTS 子查询	✅ 必须	同上
IN 子查询	❌ 不需要	子查询返回值列表，外层通过IN隐式关联
NOT IN 子查询	❌ 不需要	同上（但要注意NULL陷阱）
比较运算符子查询	❌ 不需要	如 `WHERE age > (SELECT AVG(age) ...)`
JOIN	❌ 不需要	ON子句已经处理关联

其中，特别注意 NOT IN，它可能会返回 NULL。如果表示不存在，一般使用 NOT EXISTS。

分组问题#

For each red boat, display the bid and the number of reservations for this boat.
找到所有红色船的bid和预订数量

根据题目，可以解析出：需要遍历每一艘红色船，统计每艘船的预订数量

“For each red boat” → 按红色船分组（GROUP BY）
“display the bid” → 选择 bid 列
“number of reservations” → 统计预订次数（COUNT）

1
SELECT B.bid, COUNT(R.sid) AS reservation_count
2
FROM Boat B, Reservation R
3
WHERE B.bid = R.bid AND B.color = 'red'
4
GROUP BY B.bid;

For each red boat, display the bname and the number of reservations for this boat.
找到所有红色船的bname和预订数量

这题和题目11类似，只是需要 B.bname 列。但是纯在一个陷阱：因为B.bname 不是主码，如果多艘船有相同的名字，GROUP BY 的行为会改变。

1
SELECT B.bid, B.bname, COUNT(R.sid) AS reservation_count
2
FROM Boat B, Reservation R
3
WHERE B.bid = R.bid AND B.color = 'red'
4
GROUP BY B.bid, B.bname;

这里用到了一个重要的SQL规则：SELECT 子句中的非聚合列必须出现在 GROUP BY 中

所以：

1
SELECT B.bid, B.bname, COUNT(R.sid)
2
FROM ...
3
GROUP BY B.bname;  -- ❌ 错误！bid 没在 GROUP BY 中！

至于为什么一定需要分组中添加 bid，我们通过数据来演示：

假设数据：

1
Boat:
2
bid | bname  | color
3
----+--------+------
4
101 | Sunset | red
5
103 | Sunset | red
6
105 | Storm  | red

GROUP BY B.bname:

1
SELECT B.bname, COUNT(R.sid)
2
FROM Boat B
3
LEFT JOIN Reservation R ON B.bid = R.bid
4
WHERE B.color = 'red'
5
GROUP BY B.bname;

因为只按照 bname 分组，所以结果为：

1
bname  | reservation_count
2
-------+------------------
3
Sunset | 3                  ← 101和103的预订合并了！
4
Storm  | 0

GROUP BY B.bid, B.bname（按船只和船名分组）：

1
SELECT B.bid, B.bname, COUNT(R.sid)
2
FROM Boat B
3
LEFT JOIN Reservation R ON B.bid = R.bid
4
WHERE B.color = 'red'
5
GROUP BY B.bid, B.bname;

结果：

1
bid | bname  | reservation_count
2
----+--------+------------------
3
101 | Sunset | 2
4
103 | Sunset | 1                ← 分开统计！
5
105 | Storm  | 0

所以如果需要区分不同的船只，必须在 GROUP BY 中包含主键（bid）。

总的来说，SELECT 子句中的列只能是：

聚合函数（COUNT, SUM, AVG, MAX, MIN 等）
GROUP BY 子句中的列
常量

Find the age of the youngest sailor with age > 18, for each rating with at least 2 sailors (of any age)
找出每个 rating 级别中，年龄大于18岁的最年轻水手的年龄。只考虑那些至少有2名水手 (所有年龄) 的 rating

这是一个比较复杂的题目，我们拆解它：

“for each rating” → 按 rating 分组
“with at least 2 sailors” → HAVING COUNT(*) >= 2
“(of any age)” → 统计所有船员，不限年龄
“the youngest sailor with age > 18” → MIN(age) WHERE age > 18

1
SELECT S.rating, MIN(S.age) AS youngest_age
2
FROM Sailor S
3
WHERE S.age > 18
4
  AND S.rating IN (
5
      SELECT S2.rating
6
      FROM Sailor S2
7
      GROUP BY S2.rating
8
      HAVING COUNT(*) >= 2
9
  )
10
GROUP BY S.rating;
11

12
-- 或可以在 HAVING 中嵌套子查询
13

14
SELECT S.rating, MIN(S.age) AS youngest_age
15
FROM Sailor S
16
WHERE S.age > 18
17
GROUP BY S.rating
18
HAVING 1 < (
19
  SELECT COUNT(*)
20
  FROM Sailor S2
21
  WHERE S2.rating = S.rating
22
);

分析题目可以发现：

等级条件：至少有2位船员（任何年龄）
在满足条件的等级中，找年龄 > 18的最年轻船员

这里的陷阱有：

条件”至少2名水手”是针对 所有年龄 的水手
但查找最小年龄时只考虑年龄 > 18的水手
可能存在某个rating有2名水手，但都不满足age > 18的情况

所以，我们的思路可以是：

识别符合条件的 rating：作为子查询，按 rating 分组，统计每个 rating 的水手总数，筛选出至少有2名水手的 rating。
在符合条件的 rating 中查找最小年龄，只考虑年龄>18的水手，在步骤1筛选出的rating范围内，按rating分组，找出每组的最小年龄。

这里不能直接使用：HAVING COUNT(*) >= 2 因为先执行的 WHERE 已经过滤掉了小于18岁的船员，不满足题目要求的对任意年龄而言 rating 至少为2，会出现错误答案。

Find those ratings for which the average age is the minimum overall ratings
找到年龄平均值最小的rating

这一题需要我们先按照rating进行分组，然后计算每组年龄平均值，最后取其中年龄的最小值。所以使用一个嵌套查询，外层查询计算每组年龄平均值，内层查询计算每组年龄的最小值。

1
SELECT T.rating, T.min_age    -- 不能直接使用 AVG(S.age) AS min_age 因为没有 GROUP BY 在外层
2
FROM (
3
  SELECT S.rating, AVG(S.age) AS avg_age
4
  FROM Sailor S
5
  GROUP BY S.rating
6
) AS T;
7
WHERE T.min_age = (
8
  SELECT MIN(T.avg_age)
9
  FROM T
10
);

分组问题总结#

总结一下适用于 GROUP BY 的情况：

SQL 执行顺序是：FROM → JOIN → WHERE → GROUP BY → HAVING → SELECT → DISTINCT → ORDER BY

其中我们需要记住：

WHERE 在 GROUP BY 之前（过滤 原始数据）
HAVING 在 GROUP BY 之后（过滤 分组结果）
SELECT 在 GROUP BY 之后（只能选择 分组列 或 聚合结果）

对于下面的标记，我们一般需要使用GROUP BY：

信号词	含义	示例
For each	对于每个…	For each rating, count sailors
Per	每个…	Display reservations per boat
By	按照…分组	Average age by rating
Total	总计（通常需要分组）	Total reservations for each boat
Count/Sum/Average of each	统计每个…	Sum of salaries for each department

此外，SQL 有一个重要的子句限制：SELECT 中的 非聚合列必须出现在 GROUP BY 中。

1
-- 正确示例
2
SELECT rating,           -- 在 GROUP BY 中
3
       COUNT(*),         -- 聚合函数
4
       AVG(age)          -- 聚合函数
5
FROM Sailor
6
GROUP BY rating;
7

8
-- 错误示例
9
SELECT rating,           -- 在 GROUP BY 中
10
       sname,            -- ❌ 不在 GROUP BY 中！
11
       COUNT(*)
12
FROM Sailor
13
GROUP BY rating;

我们可以从数据看到这个规则的原因：若一个 rating 中有多个船员，sname 不知道应该显示哪个。

关系代数与运算#

SQL 是结构化的关系模型操作语言，而形式化关系模型的基本操作集就是关系代数 (relational algebra)。这些操作使用户能够将基本的检索请求指定为关系代数表达式。检索查询的结果是一个新关系 (表)。

我们按照操作关系的数量和内容为关系代数进行分类，有：

一元关系 (unary operation): 选择 (select) $σ$ ，投影 (project) $π$ ，重命名 (rename) $ρ$ 。
集合关系 (set operation): 集合交 (Intersection) $\cap$ ，集合并 (Union) $\cup$ ，集合差 (Difference) $-$ ，笛卡尔积 (Cartesian product) / 叉乘 (Cross product) $\times$ 。
二元关系 (binary operation): 连接 (join) $⋈_{condition}$ ，等值连接 (equi-join) $⋈_{R . a = S . a}$ ，自然连接 (natural join) $⋈$ ，除运算 (Division) $\div$ 。

一元关系#

选择 (selection) $σ_{co n d i t i o n} (R)$ : 用于选择一个满足条件的元组。 $σ$ 可以嵌套即 $σ_{co n d i t i o n_{1}} (σ_{co n d i t i o n_{2}} (R)) = σ_{co n d i t i o n_{1} \land co n d i t i o n_{2}} (R)$ 。
投影 (projection) $π_{a tt r ib u t es} (R)$ : 用于选择一列属性。 $π$ 会进行去重。
重命名 (rename) $ρ (R, E)$ : 用于给关系 $E$ 重命名为 $R$ 。还可以为关系的属性进行重命名： $ρ (R (A_{1} \to B_{1}, A_{2} \to B_{2}, \dots), E)$ 将 $R$ 表格中的属性 $A_{i}$ 重命名为 $B_{i}$ 。

集合关系#

对于每个集合关系，要求两个关系 表格属性数相同，且对应属性的值域相同。

并集 (union) $R \cup S$ ，表示 $R$ 和 $S$ 的并集。
交集 (intersection) $R \cap S$ ，表示 $R$ 和 $S$ 的交集。
差集 (difference) $R - S$ ，表示 $R$ 和 $S$ 的差集。 $R - S = R \cup S - R \cap S$ .
叉乘 (cross product) $R \times S$ ，表示 $R$ 和 $S$ 的叉乘，包含 $R$ 和 $S$ 的所有属性和值，形成的新关系表格的属性顺序从左 ( $R$ ) 到右 ( $S$ )。

例如：

1
R：
2
| a | b |
3
----+----
4
| C | 2 |
5
| D | 3 |
6

7
S:
8
| a | c | d |
9
----+---+----
10
| A | 5 | + |
11
| B | 7 | x |

叉乘结果为：

1
R × S：
2

3
| a_R | b | a_S | c | d |
4
------+---+-----+---+----
5
| C   | 2 | A   | 5 | + |
6
| C   | 2 | B   | 7 | x |
7
| D   | 3 | A   | 5 | + |
8
| D   | 3 | B   | 7 | x |

二元关系#

连接 (join) $R ⋈_{condition} S$ ，表示 $R$ 和 $S$ 的连接，包含 $R$ 和 $S$ 的所有属性和值，形成新的关系表格。 $R ⋈_{condition} S = σ_{condition} (R \times S)$
等值连接 (equal join) $R ⋈_{R . a = S . a} S$ ，表示 $R$ 和 $S$ 根据对应字段相等的连接，不包含对应属性的列，包含 $R$ 和 $S$ 的其他列，形成新的关系表格。
自然连接 (natural join) $R ⋈ S$ ，表示 $R$ 和 $S$ 根据所有同名字段相等的连接，不包含所有同名属性的列，包含 $R$ 和 $S$ 的其他列，形成新的关系表格。

例如：

1
R:
2
| id | name   | age |
3
-----+--------+------
4
| 1  | Alice  | 18  |
5
| 2  | Bob    | 19  |
6
| 3  | Charlie| 20  |
7

8
S:
9
| id | class |
10
-----+--------
11
| 1  |   1   |
12
| 2  |   1   |
13
| 5  |   4   |

对于等值连接 $R ⋈_{R . i d = S . i d} S$ ，结果为：

1
| id | name   | age | class |
2
-----+--------+------+-------
3
| 1  | Alice  | 18  |   1   |
4
| 2  | Bob    | 19  |   1   |

该结果同样为自然连接 $R ⋈ S$ ，因为找到了所有同名字段 id 相等的元组。

除法 (Devision) $R (X, Y) \div S (Y) = T (X)$ 找出 $R$ 中那些与 $S$ 中所有 Y 值都有关联的 X 值。 $T$ 中的每个元素，都必须和 $S$ 中的每一个元素配对出现在 $R$ 中。

例如下面的学生选课问题 $R$ 和 $S$ 的例子， $T = R \div S$ 的结果为：

1
R:
2
学生   | 课程
3
-------|------
4
张三   | 数学
5
张三   | 英语
6
张三   | 物理
7
李四   | 数学
8
李四   | 英语
9
王五   | 数学
10

11
S:
12
课程
13
------
14
数学
15
英语
16

17
R / S:
18
| 学生 | 数学 | 英语 | 结果 |
19
|------|------|------|------|
20
| 张三 | ✅   | ✅   | **保留** |
21
| 李四 | ✅   | ✅   | **保留** |
22
| 王五 | ✅   | ❌   | 舍弃 |
23

24
T:
25
学生
26
------
27
张三
28
李四

除法相当于是 在 $S$ 的条件下去筛选，并且去除掉没有匹配的行以及筛选的列。它不是简单的筛选，而是跨行验证完整性。

除法适用于处理 “全部”、“所有”、“每一个”相关的查询需求。它在 SQL 中经常会被翻译为逆否命题来解决。

关系代数例题和总结#

关系代数例题#

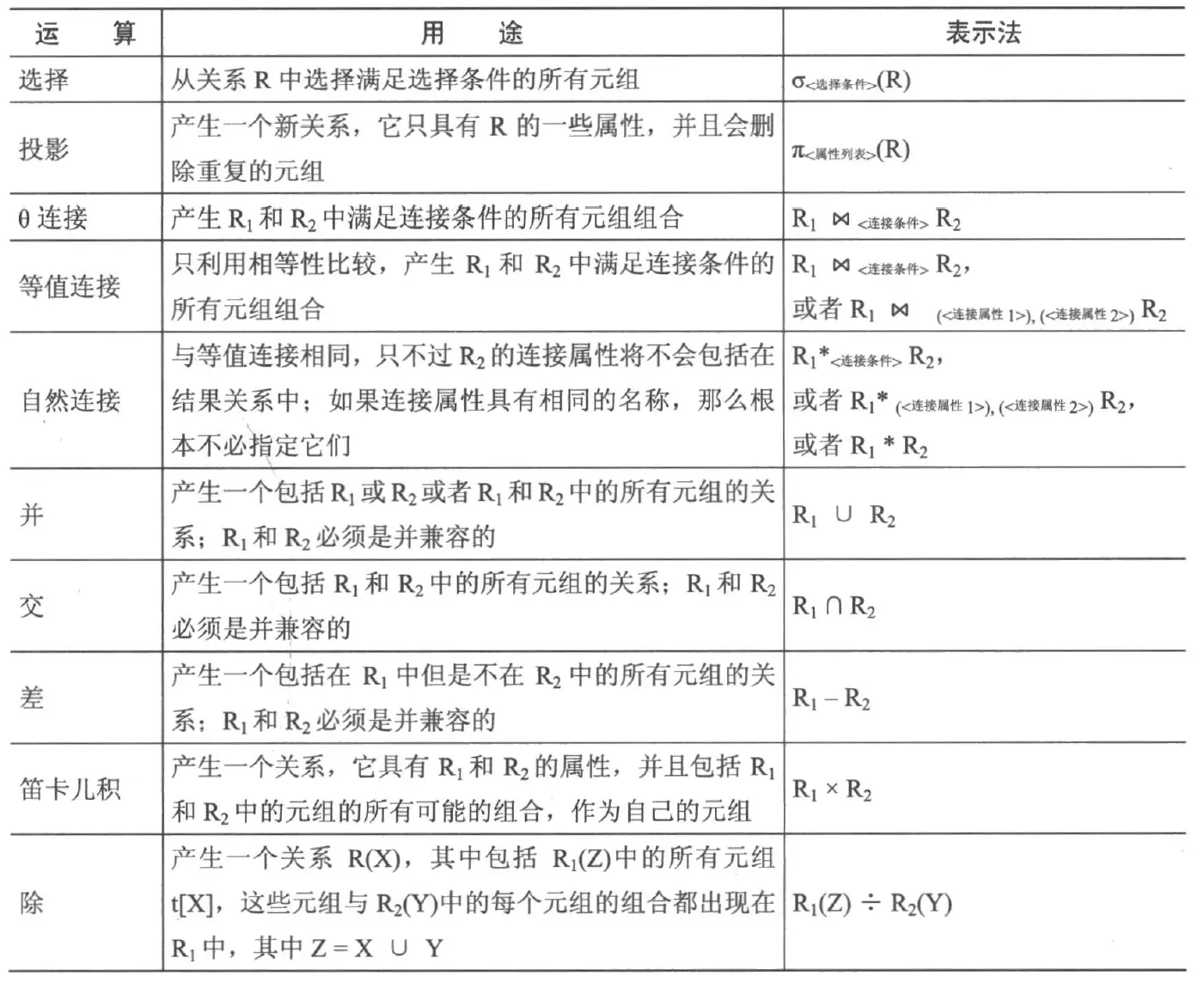
下表是关系代数的用途及其表达式的总结图：

常见的例题中，我们会将关系代数与 SQL 语句的互相转换。

Convert the following algebra expressions to SQL (for simplicity, you can omit DISTINCT):

将下列代数表达式转换为 SQL（为简化起见，可省略 DISTINCT）：
1
Employee (eid*, Ename, Salary),
2
Department (did*, Dname, eid),
3
Works(did*, eid*)
$π_{Ename} (σ_{eid = 5} (Employee))$

我们先从内层开始看，内层是一个选择语句，选择 Employee 表中 eid=5 的行。外层是个投影，只选取Ename列。

1
SELECT Ename
2
FROM Employee E
3
WHERE E.eid = 5;

$π_{eid} (Employee) - π_{eid} (Works)$

这是一个减法，即先选取 Employee 表中的所有行，再从结果中减去 Works 表中的所有行。

1
SELECT E.eid
2
FROM Employee E
3

4
EXCEPT
5

6
SELECT W.eid
7
FROM Works W;

当然，我们也可以理解为找出 没有工作分配 的员工ID：

1
SELECT E.eid
2
FROM Employee E
3
WHERE NOT EXISTS (
4
    SELECT *
5
    FROM Works W
6
    WHERE W.eid = E.eid
7
);

$π_{E.Ename} (ρ (E, Employee) ⋈ (π_{eid} (Employee) - π_{eid} (Works)))$

这一题是投影了Ename列，并使用NOT EXISTS子查询找出没有工作分配的。

1
SELECT E.Ename
2
FROM Employee E
3
WHERE NOT EXISTS (
4
    SELECT *
5
    FROM Works W
6
    WHERE W.eid = E.eid
7
);

$π_{Employee.Ename, Department.eid} (Employee ⋈ Works ⋈_{(did), (did)} Department)$

这是一个连续的自然连接和等值连接，可以很轻松得到：

1
SELECT Employee.Ename, Department.eid
2
FROM Employee E, Works W, Department D
3
WHERE Employee.eid = Works.eid AND Works.did = Department.did;

$ρ (E 1, Employee), ρ (E 2, Employee), ρ (E, Employee)$
$π_{E.Ename} (E ⋈ ((π_{E1.eid} E 1) - (π_{E1.eid} (σ_{E1.salary < E2.salary} E 1 \times E 2))))$

我们从内向外拆解：

$I = π_{E1.eid} (σ_{E1.salary < E2.salary} E 1 \times E 2)$ 是在选择满足条件的行，然后进行笛卡尔积，最后投影出 E1.eid 列。它是从笛卡尔积中选择 E1 的薪水小于 E2 的薪水的行。
$π_{E1.eid} E 1 - I$ 是从 E1 中删除 I 中的行，然后投影出 E1.eid 列。即找出 没有人薪水比自己高的员工ID（即薪水最高的员工）
$E ⋈ (π_{E1.eid} E 1 - I)$ 是进行自然连接，保留所有具有相同属性名及其值的行。即获取薪水最高的员工的 完整记录。
$π_{E.Ename} (E ⋈ I)$ 最后投影出 E.Ename 列。最后投影出员工姓名。

1
SELECT E.Ename
2
FROM Employee E
3
WHERE NOT EXISTS (
4
    SELECT *
5
    FROM Employee E2
6
    WHERE E2.Salary > E.Salary
7
);
8

9
-- 等价于
10
SELECT E.Ename
11
FROM Employee E
12
WHERE E.Salary >= ALL (
13
    SELECT E2.Salary
14
    FROM Employee E2
15
);

我们可以从内向外分析这个关系代数表达式的步骤，假设：

E1 × E2 (部分)

1
E1.eid | E1.Salary | E2.eid | E2.Salary
2
-------|-----------|--------|----------
3
1      | 5000      | 1      | 5000
4
1      | 5000      | 2      | 6000
5
1      | 5000      | 3      | 5500
6
1      | 5000      | 4      | 6000
7
2      | 6000      | 1      | 5000
8
2      | 6000      | 2      | 6000
9
2      | 6000      | 3      | 5500
10
2      | 6000      | 4      | 6000
11
...

σ_E1.salary < E2.salary (E1 × E2)

1
E1.eid | E1.Salary | E2.eid | E2.Salary
2
-------|-----------|--------|----------
3
1      | 5000      | 2      | 6000      ← Alice < Bob
4
1      | 5000      | 3      | 5500      ← Alice < Carol
5
1      | 5000      | 4      | 6000      ← Alice < David
6
3      | 5500      | 2      | 6000      ← Carol < Bob
7
3      | 5500      | 4      | 6000      ← Carol < David

π_E1.eid (...)

1
有人薪水比自己高的员工：
2
eid
3
---
4
1     (Alice)
5
3     (Carol)

差集

1
所有员工：{1, 2, 3, 4}
2
有人比自己高：{1, 3}
3
差集：{2, 4}

最终结果

1
Ename
2
-----
3
Bob
4
David

最后得到：Bob 和 David 的薪水都是 6000，是最高的，两人都被选出。

Let R(A,B,C) and S(D,E,F) be two type compatible relation schemas. Convert the following algebra expressions to SQL (for simplicity, you can omit DISTINCT):

设 R(A,B,C) 和 S(D,E,F) 是两个类型兼容的关系模式。将下列代数表达式转换为 SQL（为简化起见，可省略 DISTINCT）：

$π_{A, F} (R ⋈_{C = D} S)$

这一题内层是一个等值连接，当属性 C 的值等于属性 D 的值时，两个表行会连接起来。我们可以使用 JOIN 关键字来实现等值连接。

1
SELECT A, F
2
FROM R
3
JOIN S ON R.C = S.D;
4

5
-- 等价于
6
SELECT A, F
7
FROM R, S
8
WHERE R.C = S.D;

对于如下关系模式，* 表示主码：
1
Sailor (sid*, sname, rating, age);
2
Boat (bid*, bname, color);
3
Reservation (sid*, bid*, date*);
请找出其关系代数表达式和SQL语句。

找到预订所有的船的船员名字

我们分析题目，可以知道：找到预订了所有船的船员名字 -> (双重否定) 不存在一艘船没有被预订。这是一个典型是除法问题，因为存在关键词 “所有”。按照除法的思维，条件是所有的船，被除数就是被预定的船的信息。除出来的结果就是预定了所有的船的记录，再投影出船员名字即可。

所有船: $π_{bid} (Boat)$

1
SELECT B.bid
2
FROM Boat B;

所有被预订的船，因为最后要找到船员名字，所以需要留下 sid 去匹配船员信息。我们获取预订关系的(船员ID, 船ID)对: $π_{sid, bid} (Reservation)$

1
SELECT R.sid, R.bid
2
FROM Reservation R
3
WHERE R.bid = B.bid AND R.sid = S.sid;

执行除法，找出预订了所有船的船员ID： $π_{sid, bid} (Reservation) \div π_{bid} (Boat)$

1
SELECT B.bid
2
FROM Boat B
3
WHERE NOT EXISTS (
4
    SELECT R.sid, R.bid
5
    FROM Reservation R
6
    WHERE R.sid = S.sid
7
      AND R.bid = B.bid
8
);

与Sailor表连接并投影，并获取船员名字： $π_{sname} (S ai l or ⋈ (π_{sid, bid} (Reservation) \div π_{bid} (Boat)))$

1
SELECT S.sname
2
FROM Sailor S
3
WHERE NOT EXISTS (
4
    SELECT B.bid
5
    FROM Boat B
6
    WHERE NOT EXISTS (
7
        SELECT R.sid, R.bid
8
        FROM Reservation R
9
        WHERE R.sid = S.sid
10
          AND R.bid = B.bid
11
    )
12
);

梳理这一过程：“不存在某条船，使得该船员没有预订它”

外层NOT EXISTS：找不到反例
内层NOT EXISTS：该船员没有预订某条船

找到预订所有红船的船员名字

这一题与问题7很相似，除数从”所有船”变为”所有红船”，增加了一层条件。所以此时的除数变成是”所有红船”。

所以第一步我们要找到的是所有红船：

所有红船: $π_{bid} (σ_{color=’red’} (Boat))$

1
SELECT B.bid
2
FROM Boat B
3
WHERE B.color = 'red';

所有预订关系的(船员ID, 船ID)对： $π_{sid, bid} (Reservation)$

1
SELECT R.sid, R.bid
2
FROM Reservation R
3
WHERE R.bid = B.bid AND R.sid = S.sid;

执行除法，找出预订了所有船的船员ID： $π_{sid, bid} (Reservation) \div π_{bid} (σ_{color=’red’} (Boat))$

1
SELECT B.bid
2
FROM Boat B
3
WHERE B.color = 'red'
4
  AND NOT EXISTS (
5
      SELECT R.sid, R.bid
6
      FROM Reservation R
7
      WHERE R.sid = S.sid
8
        AND R.bid = B.bid
9
  );

与Sailor表连接并投影，并获取船员名字： $π_{sname} (S ai l or ⋈ (π_{sid, bid} (Reservation) \div π_{bid} (σ_{color=’red’} (Boat))))$

1
SELECT S.sname
2
FROM Sailor S
3
WHERE NOT EXISTS (
4
    SELECT B.bid
5
    FROM Boat B
6
    WHERE B.color = 'red'
7
      AND NOT EXISTS (
8
          SELECT R.sid, R.bid
9
          FROM Reservation R
10
          WHERE R.sid = S.sid
11
            AND R.bid = B.bid
12
      )
13
);

关系代数总结#

总结一下关系代数转换技巧：

操作类型	关系代数	SQL关键语法	转换说明
选择	$σ_{条件} (R)$	`WHERE`	根据条件筛选行，直接将关系代数的条件表达式放入WHERE子句
投影	$π_{A, B, C} (R)$	`SELECT A, B, C`	选择指定列，将下标中的属性列表放入SELECT子句
并	$R \cup S$	`UNION`	合并两个查询结果，自动去重；需保留重复则用`UNION ALL`
差	$R - S$	`EXCEPT`	返回在R中但不在S中的元组；部分数据库用`MINUS`
交	$R \cap S$	`INTERSECT`	返回同时存在于R和S中的元组
笛卡尔积	$R \times S$	`CROSS JOIN` 或 `,`	两表的所有组合，FROM子句用逗号或CROSS JOIN
θ-连接	$R ⋈_{θ} S$	`JOIN ... ON θ`	笛卡尔积+条件筛选，θ条件放入ON子句或WHERE子句
等值连接	$R ⋈_{A = B} S$	`JOIN ... ON A = B`	θ-连接的特例，连接条件为等值比较
自然连接	$R ⋈ S$	`NATURAL JOIN`	自动匹配同名属性并去重列；或手动指定公共属性等值连接
除法	$R \div S$	`NOT EXISTS` 嵌套或 `GROUP BY ... HAVING COUNT`	双重否定法：不存在S中某元组使得R中不存在匹配计数法：按R的非公共属性分组，计数等于S的元组数

常见的一些需要嵌套查询的情况：

操作	核心思路	关键词提示
除法→双重否定	找不到反例	`NOT EXISTS` 套 `NOT EXISTS`
除法→计数法	匹配数等于除数总数	`GROUP BY` + `HAVING COUNT(*) = ...`
差集→子查询	不在另一个集合中	`NOT IN` 或 `NOT EXISTS`
交集→子查询	在另一个集合中	`IN` 或 `EXISTS`

函数依赖#

在实际数据库的应用中，很容易出现存储重复数据、冗余数据、数据不一致、数据丢失等问题。

函数依赖 (Function Dependency, FD) 是一种重要的形式工具和设计理念，能够精确地检测并描述上述的一些问题。

Definition
关系模式 $R$ 的两个属性子集 $X$ 和 $Y$ 之间的函数依赖记作 $X \to Y$ ，表示 $Y$ 属性的值由 $X$ 属性决定。
若在 $X$ 上取值相同的元组在 $Y$ 上也相等，对于 $R$ 中的任意两个元组 $t_{1}$ 和 $t_{2}$ ，如果有 $t_{1} . x = t_{2} . x$ ，则 $t_{1} . y = t_{2} . y$ ，则说明 FD $X \to Y$ 成立， $X$ 决定 $Y$ 。

例如：

1
R:
2
|  A |  B |  C |  D |
3
-----+----+----+-----
4
| a1 | b1 | c1 | d1 |
5
| a1 | b2 | c1 | d2 |
6
| a2 | b4 | c2 | d1 |
7
| a3 | b1 | c3 | d3 |
8
| a4 | b2 | c1 | d4 |
9
| a4 | b3 | c1 | d5 |

我们可以发现 $R$ 中存在 FD $A \to C$ ，因为当 $t_{1} . A = t_{2} . A$ 时， $t_{1} . C = t_{2} . C$ 。注意，其中存在有 $(a_{4}, c_{1})$ 这样的元组，因为这个 对应关系和下标无关。

但是，FD $A \to C$ 不代表 $C \to A$ ，因为存在 $(c_{1}, a_{1}), (c_{1}, a_{4})$ 这样的对应关系，所以函数依赖反过来不一定成立。

若任意元组中两行的 $X$ 取值均不同，则 $X \to Y$ 称为平凡保持 (Trivial Preserved)

此时若有：

FD $X \to Y, Y \subseteq X$ ，则该 FD 称为 平凡函数依赖 (Trivial FD)。例如， ${nam e, a g e} \to {nam e}$ ，这样的FD 称为平凡函数依赖。
FD $X \to Y, Y \neq \subseteq X$ ，则该 FD 称为 非平凡函数依赖 (Non-Trivial FD)。

例如：

1
| sid | sname | cid |  cname |
2
------+------+------+---------
3
| 1   | A     | 1   |  C1    |
4
| 2   | B     | 1   |  C1    |
5
| 3   | C     | 2   |  C2    |
6
| 4   | D     | 2   |  C2    |

其中，FD ${sid, sname} \to sname$ 是一个平凡的函数依赖，因为 sname 是 {sid, sname} 的一个子集。而 FD $sid \to cname$ 则是一个非平凡的函数依赖。不能说 $cid \to sname$ 是平凡的，因为这个没有实际意义，非函数依赖。

超码和候补码#

我们已经知道了函数依赖（FD）描述的是属性之间的”决定”关系。那么，在一个关系（表）中，我们需要找出哪些属性组合能唯一标识每一行记录。这就是我们之前学到的码 (Key) 的定义。

超码 (Super Key): 能唯一标识元组的属性集合。若 $α$ 是 $R$ 的超码，则 $α \to R$ ，这里 $R$ 包含了它的所有属性的集合，表示超码能推导出所有属性，即唯一标识每个元组。
候补码 (Candidate Key): 候补码是最小的超码，满足超码定义的属性集合，且不能再通过其他属性组合得到。

例如：

1
R:
2
| A  | B  | C  | D  |
3
-----+----+----+-----
4
| a1 | b2 | c1 | d2 |
5
| a2 | b2 | c1 | d2 |
6
| a1 | b4 | c3 | d3 |
7
| a4 | b4 | c3 | d4 |

此时存在这样的函数依赖： $AC \to R$ , $AD \to R$ , $ACD \to R$

$AC \to R$ : 此时 AC 中每一个元组均唯一 {a1c1, a2c1, a1c3, a4c3}，它们满足任何 AC 中 具有的值相等的元组，在 R 中的值都相等，这一条件满足超码定义，故 AC 为超码。若删除 A 或 C 后，它们 均无法唯一标识每个元组，则 AC 是候补码。
$AD \to R$ : 同理，AD 中每一个元组均唯一 {a1d2, a2d2, a1d3, a4d4}，它们满足任何 AD 中 具有的值相等的元组，在 R 中的值都相等，这一条件满足超码定义，故 AD 为超码。若删除 A 或 D 后，它们 均无法唯一标识每个元组，则 AD 是候补码。
$ACD \to R$ : 同理，ACD 中每一个元组均唯一 {a1d2, a2d2, a1d3, a4d4}，它们满足任何 ACD 中 具有的值相等的元组，在 R 中的值都相等，这一条件满足超码定义，故 ACD 为超码。但 AC 和 AD 组合均满足超码定义，故 ACD 不是候选码。

我们把一个关系的所有函数依赖的集合称为关系 R 的 函数依赖集 (Function Dependency set)，记为 $F$ 。例如： $F = {A \to B, A \to C, B \to D}$ 。

如果说一个函数依赖 $f \in / F$ ，且能被 $F$ 中的函数依赖所推导出来，则称 $f$ 被 $F$ 蕴含 (Imply)。例如， $f = A \to D$ 被 $F$ 蕴含，因为 $A \to B, B \to D$ 表示 $A$ 能确定 $B$ ， $B$ 可以确定 $D$ ，故 $A$ 可以确定 $D$ 。

闭包#

从函数依赖集 $F$ 出发，通过推理规则能够推导出的其他函数依赖（包括F本身）。我们将推导结果的集合其称为 $F$ 的闭包 ( $F^{+}$ Closure)，记作 $F^{+}$ 。它是所有可以从 $F$ 推导出来的函数依赖的集合。

推导 $F$ 闭包的核心工具是 Armstrong 公理，它有如下的规则：

自反律 (Reflexivity): 如果 $Y \subseteq X$ ，则 $X \to Y$ 。例如 ${A, B, C} \to {A, C}$
增广律 (Augmentation): 如果 $X \to Y$ ，则 $XZ \to Y Z$ （对任意属性集 $Z$ ）。例如： $A \to B$ ，则 $A C \to BC$
传递律 (Transitivity): 如果 $X \to Y, Y \to Z$ ，则 $X \to Z$ 。例如： $A \to B$ ， $B \to C$ ，则 $A \to C$

还有三个派生规则：

合并律 (Union): 如果 $X \to Y$ 且 $X \to Z$ ，则 $X \to Y Z$
分解律 (Decomposition): 如果 $X \to Y Z$ ，则 $X \to Y$ 且 $X \to Z$
部分传递律 (Partial Transitivity): 如果 $X \to Y$ 且 $WY \to Z$ ，则 $X W \to Z$

我们一般使用前三条规则就可以找到 $F$ 的闭包了。

例如，

$F = {A \to B, B \to C}$ , $R = {A, B, C}$ ，求 $F$ 的闭包 $F^{+}$ ：

我们先添加 $R$ 属性自身： $F^{+} = {A \to A, B \to B, C \to C}$
开始逐步运用三大定律和已有的 $F$ ： $F^{+} = {\dots, A \to C (传递), A B \to B (自反, A C \to BC (增广)), \dots}$

最后得到结果：

F^{+} = {A \to A, A \to B, A \to C, A \to A B, A \to A C, A \to BC, A \to A BC, B \to B, B \to C, B \to BC, C \to C, A B \to A, A B \to B, A B \to C, A B \to A B, A B \to A C, A B \to BC, A B \to A BC, A C \to A, A C \to B, A C \to C, A C \to A B, A C \to A C, A C \to BC, A C \to A BC, BC \to B, BC \to C, BC \to BC, A BC \to A, A BC \to B, A BC \to C, A BC \to A B, A BC \to A C, A BC \to BC, A BC \to A BC}

属性闭包 (Attribute Closure) 是 $F^{+}$ 的一个子集 $X^{+}$ ，表示从属性集 $X$ 出发，利用函数依赖集 $F$ 中的规则，能够直接或间接确定（推导出）的所有属性的集合。

例如：

$F = {A \to B, B \to C}$ ，求属性闭包 $A^{+}$

初始化自身属性： $A^{+} = {A}$
遍历每个函数依赖，若属性未被加入，则加入该属性并计算其闭包：
- 对于 $A \to B$ ， $B$ 不在闭包中，则加入 $A^{+} = {A} \cup {B} = {A B}$
- 计算 $B^{+}$ : $B^{+} = {B} \cup {C} = {BC}$ ，则加入 $A^{+} = {A B} \cup {BC} = {A BC}$
- 计算 $C^{+} :$ $C^{+} = {C}$ ，则加入 $A^{+} = {A BC}$

最后，我们得到了 $A^{+} = {A BC}$

还有一个组合属性集的例子，给定：

1
R(A, B, C, D), F = {AB → C, C → D}

计算 ${A}^{+}$ :

1
初始化：result = {A}
2

3
第1轮：
4
  - AB → C：{A, B} ⊄ {A} ✗（缺B）
5
  - C → D：C ⊄ {A} ✗
6

7
结果：{A}⁺ = {A}

计算 ${A,B}^{+}$ ：

1
初始化：result = {A, B}
2

3
第1轮：
4
  - AB → C：{A, B} ⊆ {A, B} ✓ → result = {A, B, C}
5
  - C → D：C ⊆ {A, B, C} ✓ → result = {A, B, C, D}
6

7
第2轮：
8
  - 无新属性可加
9

10
结果：{A, B}⁺ = {A, B, C, D} = R

函数依赖例题和总结#

函数依赖例题#

在实际情况中，我们一般只会看到表格的部分记录，因此我们一般会讨论函数 $f$ 是否满足函数依赖关系，请你根据下面的元组，给出5个不满足函数依赖关系的 $f$ 。
1
| A  | B  | C  |
2
| -  | -  | -  |
3
| a1 | b1 | c1 |
4
| a1 | b1 | c2 |
5
| a2 | b1 | c1 |
6
| a2 | b1 | c3 |

根据函数依赖的定义： $f = {X} \to {Y}$ 满足函数依赖关系，当且仅当 $f$ 中的属性值 $X$ 和 $Y$ 对于任意元组 $t_{1}, t_{2}$ 满足 $t_{1} [X] = t_{2} [X]$ 时， $t_{1} [Y] = t_{2} [Y]$ 。

我们可以举出如下不满足函数依赖关系的例子：

$f = {B} \to {A}$
$f = {C} \to {A}$
$f = {B} \to {C}$
$f = {A} \to {C}$
$f = {A, B} \to {C}$

$R = Title, Theater, City$ 其中，Title 是电影的名字，Theater 是电影院的名字，City 是电影院所在的城市。

现在有如下限制：

不同的城市不会存在两个相同名字的电影院。

一个城市中的不同电影院不会播放相同的电影。

一个电影院可以播放多个电影。

请你找到限制中隐藏的函数依赖关系。

我们可以逐条转化这些自然语言限制：

“不同的城市不会存在两个相同名字的电影院”: Theater → City。
“一个城市中的不同电影院不会播放相同的电影”: 在同一个城市，电影和电影院是一一对应的
“一个电影院可以播放多个电影”: 说明 Theater 不能唯一确定 Title

那我们可以推导出：

Theater → City: 知道电影院，就可以知道城市
City, Title → Theater: 同一城市 + 同一电影 → 必定是同一个电影院

我们可以逐一计算其属性闭包：

$Title^{+}$ :
- 对于 Theater → City, $Theater \neq \subseteq Title$ ；
- 对于 City, Title → Theater, ${City, Title} \neq \subseteq Title$ 。
所以 $Title^{+} = {Title}$ 。
$Theater^{+}$ :
- 对于 Theater → City， $Theater \subseteq {Theater}$ ，所以 $Theater^{+} = {Theater, City}$ ；
- 对于 City, Title → Theater, ${City, Title} \neq \subseteq {Theater, City}$ 。
所以 $Theater^{+} = {Theater, City}$ .
$City^{+}$ :
- 对于 Theater → City, $Theater \neq \subseteq {City}$ ；
- 对于 City, Title → Theater, ${City, Title} \subseteq {City}$ 。
所以 $City^{+} = {City}$ .

观察一下这两个函数依赖，我们可以发现 FD2 City, Title → Theater 可以结合 FD1 Theater → City 运用传递律得到：City, Title → City，这是一个平凡FD。同理，可以推导出 City, Title → Title，所以 City, Title → Title, Theater, City = R，此时 City, Title 是一个超码，根据三个属性的闭包均不等于 $R$ 可知，它是一个候选码。

此外，我们对 FD1 运用增广律，可以得到 Title, Theater → Title, City，再加上自身属性 Title, Theater，它也是一个候选码。

当然我们也可以使用比较规范的方法求候选码，该方法记录在该章节的总结部分：函数依赖总结。

先找到四种属性分类：

L (只在 FD 左侧出现): $Title$
R (只在 FD 右侧出现): $\emptyset$
N (不在 FD 中出现): $\emptyset$
LR (既在 FD 左侧又在 FD 右侧出现): $City, Theater$

所以，L 的属性 $Title$ 是候选码的一部分。接下来组合验证：

$Title \cup City$ : 求它的属性闭包，很明显可以得到 $(Title, City)^{+} = R$ ，所以 $(Title, City)$ 是一个候选码。
$Title \cup Theater$ : 同上， $(Title, Theater)^{+} = R$ ，所以 $(Title, Theater)$ 也是一个候选码。

我们想要创新一个数据库去存储银行的账户信息 Accounts (A), 分支信息 Branches (B) 和客户信息 Customers (C)，并满足下面给出的限制。

一个账户不会被多个客户共享。

两个不同的分支不会拥有相同的账户。

一个用户在一个支行只能拥有一个账户，但可以在不同的支行拥有不同的账户。

请你找到限制中隐藏的函数依赖关系。

解析这些限制关系：

“一个账户不会被多个客户共享”: 这意味着一个账户只能对应一个客户，A → C。
“两个不同的分支不会拥有相同的账户”: 这意味着一个账户只能对应一个分支，A → B。
“一个用户在一个支行只能拥有一个账户，但可以在不同的支行拥有不同的账户”: 这意味着一个用户和一个支行能确定一个账户，{C, B} → A。

所以我们可以推导出：

A → C: 账户只能对应一个客户
A → B: 账户只能对应一个分支
{C, B} → A: 一个用户和一个支行能确定一个账户

接下来我们来找出该数据库的候选码，首先找出单属性闭包：

$A^{+}$ :
- A → C: ${A} \subseteq {A}$ ，所以 $A^{+} = {A, C}$ .
- A → B: 同上， $A^{+} = {A, B, C}$
- {C, B} → A: ${C, B} \neq \subseteq {A}$ ，没有属性需要加入。
所以 $A^{+} = {A, B, C} = R$ .
$B^{+}$ :
- A → C: ${A} \neq \subseteq {B}$
- A → B: ${A} \neq \subseteq {B}$
- {C, B} → A: ${C, B} \neq \subseteq {B}$
所以 $B^{+} = {B}$ .
$C^{+}$ :
- A → C: ${A} \neq \subseteq {C}$
- A → B: ${A} \neq \subseteq {C}$
- {C, B} → A: ${C, B} \neq \subseteq {C}$
所以 $C^{+} = {C}$ .

可以发现， $A^{+} = R$ 是一个候选码。接下来考虑两个属性的闭包，这里省略了。

可以发现， ${C, B} \to A, A \to R ⟹ {C, B} \to R$ ，它的两个子属性闭包不等于 $R$ ，所以 ${C, B}$ 也是一个候选码。

$R = {A, B, C}$ 我们不知道它的码是什么，如果 $A$ 是一个候选码，你会怎么样去检测它？使用 SQL 语句去检测。

如果 $A \to B$ 是一个函数依赖，请你使用 SQL 语句去检测它。

回顾码的定义: 码是一个能够唯一标识一个元组的属性集合。码属性的数量等于所有元组的数量。

那么我们使用 GROUP BY 得到的结果，每一组都是一个元组。

1
SELECT A
2
FROM R
3
GROUP BY A
4
HAVING COUNT(*) > 1;

如果结果是空，则 $A$ 是一个候选码。
如果结果不为空，则 $A$ 不是一个候选码。

对于 $A \to B$ ，说明 $A$ 属性能唯一确定 $B$ 属性的值。那么我们只需要按照 $A$ 进行分组，其中每个组只有一个 $B$ 属性值则关系成立。

1
SELECT A
2
FROM R
3
GROUP BY A
4
HAVING COUNT(DISTINCT B) > 1;

如果结果是空，则 $A \to B$ 是 FD。
如果结果不为空，则 $A \to B$ 是 FD。

对于 $R = {X, Y, U, V, W}$ ，有如下的函数依赖： $X \to Y, {U, V} \to W, V \to X$ ，找到每个单属性闭包。

$X^{+}$ :
- X → Y: ${X} \subseteq {X}$ , 所以 $X^{+} = {X, Y}$ .
- {U, V} → W: ${U, V} \neq \subseteq {X, Y}$ , 没有属性需要加入。
- V → X: ${V} \neq \subseteq {X, Y}$ , 没有属性需要加入。

所以 $X^{+} = {X, Y}$ .

$Y^{+}$ :
- X → Y: ${X} \neq \subseteq {Y}$ , 没有属性需要加入。
- {U, V} → W: ${U, V} \neq \subseteq {Y}$ , 没有属性需要加入。
- V → X: ${V} \neq \subseteq {Y}$ , 没有属性需要加入。

所以 $Y^{+} = {Y}$ .

$U^{+}$ :
- X → Y: ${X} \neq \subseteq {U}$ , 没有属性需要加入。
- {U, V} → W: ${U, V} \neq \subseteq {U}$ , 没有属性需要加入。
- V → X: ${V} \neq \subseteq {U}$ , 没有属性需要加入。

所以 $U^{+} = {U}$ .

$V^{+}$ :
- X → Y: ${X} \neq \subseteq {V}$ , 没有属性需要加入。
- {U, V} → W: ${U, V} \neq \subseteq {V}$ , 没有属性需要加入。
- V → X: ${V} \subseteq {V}$ , 所以 $V^{+} = {V, X}$ .
- 重新检测 X → Y: ${X} \subseteq {V, X}$ ，所以 $V^{+} = {V, X, Y}$ .
- 重新检测 {U, V} → W: ${U, V} \neq \subseteq {V, X, Y}$ , 没有属性需要加入。
- 重新检测 V → X: ${V} \subseteq {V, X, Y}$ ，但 $X$ 已经在闭包中，无需加入。

所以 $V^{+} = {V, X, Y}$ .

$W^{+}$ :
- X → Y: ${X} \neq \subseteq {W}$ , 没有属性需要加入。
- {U, V} → W: ${U, V} \neq \subseteq {W}$ , 没有属性需要加入。
- V → X: ${V} \neq \subseteq {W}$ , 没有属性需要加入。

所以 $W^{+} = {W}$ .

函数依赖总结#

我们来总结一下函数依赖相关的问题的步骤和技巧：

函数依赖 (Functional Dependency, FD)： $X \to Y$ 如果知道了 $X$ 的值，就能唯一确定 $Y$ 的值。我们还有如下重要概念：

概念	定义	示例
平凡依赖	Y ⊆ X 的函数依赖	`{A, B} → A`
非平凡依赖	Y ⊄ X 的函数依赖	`A → B`
推导函数依赖	Y 依赖于 X，但不依赖于 X 的任何真子集	`{学号,课程} → 成绩`

常见的题型是：根据数据库限制找函数依赖和候补码。

常见的有如下关键词表示 函数依赖关系：

现实数据库限制	含义	FD模式	实例句子
X has a unique Y	X有唯一的Y	X → Y	Course has a unique course code
X has only one Y	X只有一个Y	X → Y	Employee has only one manager
for each X, there is only one Y	对每个X只有一个Y	X → Y	For each student, there is only one major
each X has a fixed Y	每个X有固定的Y	X → Y	Each course has a fixed credit value
given X, we can determine Y	给定X可确定Y	X → Y	Given ISBN, we can determine title

下面表格总结了一些 非函数依赖关系的标识：

现实数据库限制	含义	FD模式	实例句子
X can have multiple Y	X可以有多个Y	X ↛ Y	Professor can have multiple courses
X may have many Y	X可能有多个Y	X ↛ Y	Student may have many hobbies
X has several Y	X有多个Y	X ↛ Y	Author has several books
X and Y are many-to-many	X和Y是多对多	X ↛ Y, Y ↛ X	Students and courses are many-to-many
Y varies independently of X	Y独立于X变化	X ↛ Y	Supplier price varies independently of product
Y is independent of X	Y独立于X	X ↛ Y	Birth date is independent of salary
multiple X can share same Y	多个X可共享同一Y	X ↛ Y	Multiple employees can share same office

我们需要找到候选码，先回顾码的定义：

Superkey（超码）：能唯一标识元组的属性集
Candidate Key（候选码）：最小超码（minimal superkey）

我们可以将属性分为四类：

类别	定义	特点
L（Left）	只出现在 FD 左边	必然在候选码中
R（Right）	只出现在 FD 右边	不可能在候选码中
N（Neither）	两边都不出现	必然在候选码中
LR（Both）	两边都出现	可能在候选码中

对于关系 $R (A_{1}, A_{2}, \dots, A_{n})$ , 函数依赖集 $F$ :

Step 1: 属性分类：计算 L, R, N, LR 类属性
Step 2: 初始候选码： $Base = L \cup N$ (这些属性必须在候选码中)
Step 3: 检验 Base: 计算 $Base^{+}$ ，如果 $Base^{+} = R$ ，则 Base 是唯一候选码。否则添加 LR 属性，对 LR 类属性的每个子集 S：计算 $(Base \cup S)^{+}$ ，如果等于所有属性则是候选码。

例如：

1
关系：R(A, B, C, D, E)
2
FD：F = {A → B, BC → E, ED → A}
3

4
Step 1: 分类
5
  L: {C, D}      (只在左边)
6
  R: {}         (只在右边)
7
  N: {}          (两边都不出现)
8
  LR: {A, B, E}     (两边都出现)
9

10
Step 2: Base = {C, D}
11

12
Step 3: 计算 {C,D}⁺
13
  {C,D}⁺ = {C,D}  (不能推导更多属性)
14
  不是候选码，需要添加 LR 属性
15

16
Step 4: 尝试添加 A 或 E
17
  - {C,D,A}⁺ = {C,D,A,B,E} ✓ 是超码
18
    检查最小性：
19
    - {C,D}⁺ = {C,D} ✗
20
    - {C,A}⁺ = {C,A,B} ✗
21
    - {D,A}⁺ = {D,A,B} ✗
22
    → {C,D,A} 是候选码
23

24
  - {C,D,B}⁺ = {C,D,B,E,A} ✓ 是超码
25
    检查最小性：
26
    - {B,C}⁺ = {B,C,E} ✗
27
    - {B,D}⁺ = {B,D} ✗
28
    → {C,D,B} 是候选码
29

30
  - {C,D,E}⁺ = {C,D,E,A,B} ✓ 是超码
31
    检查最小性：
32
    - {C,E}⁺ = {C,E} ✗
33
    - {D,E}⁺ = {D,E,A,B} ✗
34
    → {C,D,E} 是候选码
35

36
结论：候选码为 {CDA}, {CDB}, {CDE}

对于求属性闭包的问题，我们一般采取以下示例中的步骤：

有一个数据库： $R (A, B, C, D, E)$ , $F = A \to BC, C D \to E, B \to D, E \to A$ ，求 ${A}^{+}$

先取自反: ${A}^{+} = {A}$
检查 $A \to BC$ : 发现 $A$ 属于当前闭包，加入后续属性到闭包中： ${A}^{+} = {A, B, C}$
可以直接检查 $B \to D$ ，因为 $B$ 属于当前闭包: ${A}^{+} = {A, B, C, D}$
检查 $C D \to E$ ，因为此时 $C D$ 均在闭包中，需要重新检查其他函数依赖: ${A}^{+} = {A, B, C, D, E}$
检查 $E \to A$ ，无元素可以添加: ${A}^{+} = {A, B, C, D, E}$

结果： ${A}^{+} = {A, B, C, D, E}$ ， $A$ 是候选码。

范式化#

范式#

范式 (Normal Form, NF) 是在数据库设计中遵循的一系列规则，以确保数据结构的优化。

数据库中提出了 4 种常见的范式：1NF, 2NF, 3NF, BCNF

1NF：每个属性都是 原子的（atomic），不可再分。即不存在多值属性或嵌套属性。
2NF：满足 1NF，并且非主属性 (除主码之外的属性) 必须完全依赖于候选码。即不存在非主属性的部分依赖。
3NF：满足 2NF，并且非主属性不能有传递依赖。即 3NF 要求每一个非主属性都与候选码直接相关，而不是间接相关。
BCNF (Boyce-codd Normal Form)：满足 3NF，并且满足 $R$ 中存在一个 非平凡依赖 $X \to A$ ( $A \neq \subseteq X$ ), 且 $X$ 是 $R$ 的超码，则 $R$ 属于 BCNF。

其中 2NF 和 3NF 提到的两个依赖的概念：

部分依赖 (Partical Dependency)：一个函数依赖关系形如： ${X, Y} \to Z$ ，若存在子集 $S$ ( $X$ 或 $Y$ )，使得 $S \to Z$ ，则称 $Z$ 部分依赖 于 ${X, Y}$ 。
传递依赖 (Transitive Dependency)：函数依赖关系形如： $A \to B, B \to C$ ，则称 $A \to C$ 是 传递依赖。

我们主要关注 3NF 和 BCNF，因为 3NF 和 BCNF 是数据库中最常用的范式。

重新关注这两个范式，我们可以得到：

BCNF: 若 $R$ 属于 BCNF，对于任意 ${X \to A} \subseteq F$ ，满足:
1. $X \to A$ 是 平凡依赖，或
2. $X$ 是 $R$ 的超码。
3NF: 若 $R$ 属于 3NF，对于任意 ${X \to A} \subseteq F$ ，满足:
1. $X \to A$ 是 平凡依赖，或
2. $X$ 是 $R$ 的超码，或
3. $A$ 为 某个候选键的一部分。

例如：

$R = (A, B, C), F = {A \to B, B \to C}, k ey = {A}$ ，判断是否属于 BCNF。

对于 ${A \to B}$ ， $A$ 是 $R$ 的码；
对于 ${B \to C}$ ，不存在平凡依赖 ( $C \neq \subseteq B$ ) 且 $B$ 不为码，所以 $R$ 不属于 BCNF。

$R = (A, B, C, D, F), F = {A E \to BC D, D \to A}, k ey = {A E, D E}$ ，判断是否属于 3NF。

对于 ${A E \to BC D}$ ， $A E$ 是 $R$ 的码；
对于 ${D \to A}$ ，不存在平凡依赖 ( $A \neq \subseteq D$ )， $D$ 不为码， $A$ 是码 $A E$ 的一部分。

所以 $R$ 属于 3NF。

分解#

我们知道怎么判断一个关系模式 $R$ 是否属于某个范式后，对于不合格的关系模式，我们可以进行分解 (Decomposition)，将关系模式分解为多个关系模式，使得这些关系模式都满足该范式。

对于 3NF 而言，我们有两种常见的分解方法：

无损连接分解 (Lossless Join Decomposition): 将一个关系模式经过分解后通过自然连接能恢复原关系。即， $R ⟹ R_{1} \land R_{2}, R_{1} ⋈ R_{2} = R$ 。根据这个条件，我们还可以推导出：两个分解关系的公共属性 ( $R_{1} \cap R_{2}$ ) 必须是其中 至少一个关系 ( $R_{1}$ 或 $R_{2}$ ) 的超码。这意味着： $R_{1} \cap R_{2} \to R_{1} - R_{2}$ 或 $R_{1} \cap R_{2} \to R_{2} - R_{1}$ 。
保持依赖分解 (Dependency Preserving Decomposition): 将一个关系模式分解为多个关系模式，使得这些关系模式满足依赖关系。即， $R ⟹ R_{1} \land R_{2}, (F_{1} \cup F_{2})^{+} = F^{+}$

例如：

$R (sid *, sname, major)$ ，分解为 $R_{1} (sid *, sname), R_{2} (sid *, major)$ ，请判断是否为无损连接分解。若分解为 $R_{3} (sid *, sname), R_{4} (sname, major)$ ，请判断是否为无损连接分解。

对于 $R_{1}$ 和 $R_{2}$ ，我们计算 $R_{1} ⋈ R_{2} = (sid *, sname, major) = R$ ，所以它是一个无损连接分解。

对于 $R_{3}$ 和 $R_{4}$ ，我们计算 $R_{3} ⋈ R_{4} = (sid *, sname, major)$ ，但是自然连接的条件 $sname$ 并非 $R$ 的候选码，连接的数据可能不一致，所以它不是一个无损连接分解。

$R (sid *, sname, major)$ ，若 $F = {sid \to sname, sname \to major}$ 。分解为 $R_{1} (sid *, sname), R_{2} (sid *, major)$ ，请判断是否为保持依赖分解。若分解为 $R_{3} (sid *, sname), R_{4} (name, major)$ ，请判断是否为保持依赖分解。

对于 $R_{1}$ 和 $R_{2}$ ， $F_{1} = {sid \to sname}$ ， $F_{2} = {sid \to major}$ ， $(F_{1} \cup F_{2}) = {sid \to sname, sid \to major}$ , $F = {sid \to sname, sname \to major}$ ， $(F_{1} \cup F_{2})^{+} \neq = F^{+}$ ，所以它不是一个保持依赖分解。

对于 $R_{3}$ 和 $R_{4}$ ， $F_{3} = {sid \to sname}$ ， $F_{4} = {sname \to major}$ ， $(F_{3} \cup F_{4}) = {sid \to sname, sname \to major}$ , $F = {sid \to sname, sname \to major}$ ， $(F_{3} \cup F_{4})^{+} = F^{+}$ ，它是一个保持依赖分解。

对于 BCNF，我们可以使用无损连接分解，但是 不能使用保持依赖分解。我们一般将 BCNF 分解称为 规范化 (Normalization)。

下面是 BCNF 分解的算法步骤：

1
输入：R, F
2
输出：BCNF分解
3

4
Algorithm (递归)：
5
If R 不在 BCNF:
6
  找一个违反的 FD (X→Y)，其中 X 不是超码
7
  分解为：
8
    R1 = X ∪ Y
9
    R2 = R - (Y - X)
10
  递归分解 R1 和 R2
11
Else:
12
  返回 R

我们通过一个例子来解析这个过程：

$R = (A, B, C, D, E), F = {A \to B, A \to D, C \to E}$ ， $Key = {A C}$ ，请判断 $R$ 是否为 BCNF，若不是，请分解为 BCNF。

我们先判断其是否为 BCNF：

对于 ${A \to B}$ ， $A$ 不是 $R$ 的码，违反 BCNF 条件。
对于 ${A \to D}$ ， $A$ 不是 $R$ 的码，违反 BCNF 条件。
对于 ${C \to E}$ ， $C$ 不是 $R$ 的码，违反 BCNF 条件。

所以 $R$ 不属于 BCNF。

接下来开始执行算法去分解它为 BCNF：

分解 $R = (A, B, C, D, E)$ ：选择 ${A \to B}$ ，分解为 $R_{1} = (A \cup B) = (A, B)$ ， $R_{2} = R - (B - A) = (A, C, D, E)$ . 接下来，递归分解 $R_{1}$ 和 $R_{2}$ 。
1. 对于 $R_{1}$ ，投影到 $R_{1}$ 的 FD 为： $A \to B$ ， $A^{+} = {A, B} = R_{1}$ ， $R_{1}$ 满足 BCNF 条件。
2. 对于 $R_{2}$ ，投影到 $R_{2}$ 的 FD 为： ${A \to D, C \to E}$ ，对于 ${A \to D}$ ， $A$ 不是 $R_{2}$ 的码 $A C$ ，违反 BCNF 条件；对于 ${C \to E}$ ， $C$ 不是 $R$ 的码，违反 BCNF 条件。 $R_{2}$ 不属于 BCNF，需要继续分解。
分解 $R_{2} = (A, C, D, E)$ ：选择 ${A \to D}$ ，分解为 $R_{3} = (A \cup D) = (A, D)$ ， $R_{4} = R_{2} - (D - A) = (A, C, E)$ .
1. 对于 $R_{3}$ ，投影到 $R_{3}$ 的 FD 为： $A \to D$ ， $A^{+} = {A, D} = R_{3}$ ， $R_{3}$ 满足 BCNF 条件。
2. 对于 $R_{4}$ ，投影到 $R_{4}$ 的 FD 为： ${C \to E}$ ， $C$ 不是 $R$ 的码，违反 BCNF 条件。 $R_{4}$ 不属于 BCNF，需要继续分解。
分解 $R_{4} = (A, C, E)$ ：选择 ${C \to E}$ ，分解为 $R_{5} = (C \cup E) = (C, E)$ ， $R_{6} = R_{4} - (E - C) = (A, C)$ .
1. 对于 $R_{5}$ ，投影到 $R_{5}$ 的 FD 为： $C \to E$ ， $C^{+} = {C, E} = R_{5}$ ， $R_{5}$ 满足 BCNF 条件。
2. 对于 $R_{6}$ ，投影到 $R_{6}$ 的 FD 无非平凡依赖，满足 BCNF 条件。

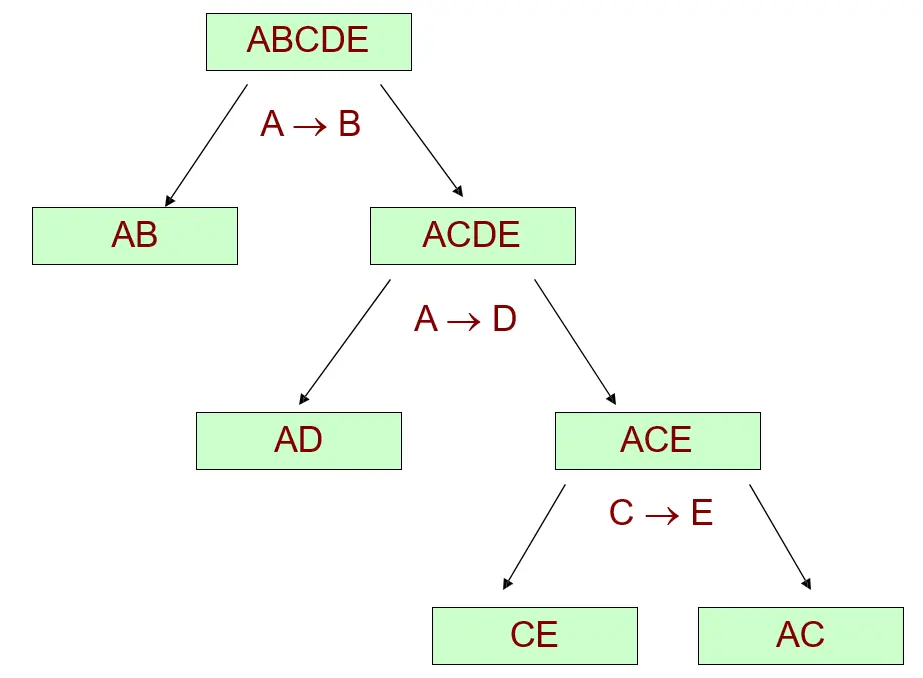
至此， $R$ 被分解为 $R_{1}, R_{2}, R_{3}, R_{4}, R_{5}, R_{6}$ 6 个属于BCNF 的关系模式，它们的分解过程图如下：

范式例题和总结#

范式例题#

对于范式化这一章节，主要考点是判断当前关系模式是否为 3NF 或 BCNF，判断其是否能被无损连接分解，或能否被保持依赖分解，以及递归分解为BCNF 的算法。

在此之前，我们需要找出当前关系模式的所有函数依赖及其候选码，在上一章的例题中一题提到，可以跳转查看：函数依赖例题和总结

如果有这样的关系模式 $R = (Customer, Store, Product, Price)$ 有如下的限制：

一个用户只会从一个商店购买商品。

一个商店中的一个商品只能有一个价格。

请你找到蕴含的所有函数依赖关系和候选码，并判断当前关系模式是否为 3NF 或 BCNF。

运用函数依赖的知识，我们可以分析：

一个用户只会从一个商店购买商品：一个用户对应一个商店，一个商店可以有多个用户。 $Customer \to Store$
一个商店中的商品只能有一个价格：一个商店中的一个商品只能有一个价格，价格由商店和商品决定。 $Store, Product \to Price$

所以， $F = {Customer \to Store, {Store, Product} \to Price}$

我们列出 $F$ 相关的四类属性：

L: ${Customer}$
R: ${Price}$
N: $\emptyset$
LR: ${Store}, {Product}$

所以， ${Customer}$ 是部分码。

加入 ${Store}$ 后，得到 ${Customer, Store}$ ， ${Customer, Store}^{+} = {Customer, Store} \neq = R$ ，所以它不是候选码。
加入 ${Product}$ 后，得到 ${Customer, Product}$ ，计算 ${\text{Customer, Product}}^+：
- $Customer \to Store$ : 加入 ${Store}$ 得到 ${Customer, Product, Store}$
- $Store, Product \to Price$ : 加入 ${Price}$ 获得 ${Customer, Product, Store, Price} = R$

所以 ${Customer, Product}$ 是唯一的候选码。

接下来我们判断当前关系模式是否为 3NF 或 BCNF。

对于 $Customer \to Store$ ，不存在平凡依赖， $Customer$ 不是 $R$ 的超码，但是码的一部分。
对于 ${Store, Product} \to Price$ ，不存在平凡依赖， $Store, Product$ 不是 $R$ 的超码，也不是 $R$ 的码的一部分。

所以，当前关系模式既不属于 3NF，也不属于 BCNF。

若 $R = (A, B, C, D, E), F = {A \to BC, C \to D}$ ，它分解为 $R_{1} = (A, B, C), R_{2} = (A, D, E)$ 。请你判断：

该分解是否为 无损连接分解？

该分解是否为 保持依赖分解？

该分解是否为 BCNF 分解？

是否可以 BCNF 分解 的情况下保持依赖关系？

对于这样的关系模式，我们先要分析其候选码：

L: ${A}$
R: ${B}, {D}$
N: ${E}$
LR: ${C}$

于是， ${A, E}$ 是部分码。测试 ${A, E}^{+}$ 。

${A, E}^{+} = {A BC D E} = R$

所以， ${A E}$ 是唯一候选码。

观察 $F$ ，可以发现其中蕴藏着隐藏的函数依赖关系：

$A \to C, C \to D ⟹ A \to D$

对于无损连接分解，我们测试 $R_{1} ⋈ R_{2} = (A, B, C, D, E) = R$ ，并且要求 $R_{1} \cap R_{2} = A$ ， $A$ 至少是 $R_{1}$ 或 $R_{2}$ 的超码。
1. 我们验证 $R_{1}$ ：它投影到的 FD: ${A \to BC}$ ，很明显 $A$ 是 $R_{1}$ 的候选码。
2. 对于 $R_{2}$ ：它投影到的 FD: ${A \to D}$ ，很明显 $E$ 一定在候补码中， $A$ 不是 $R_{2}$ 的候选码。
当前分解满足：公共属性 $A$ 是 $R_{1}$ 的超码，所以该分解为无损连接分解。
对于保持依赖分解， $F_{1} = {A \to BC}$ ， $F_{2} = {A \to D}$ ， $(F_{1} \cup F_{2})^{+} = {A \to BC, A \to D}^{+} \neq = F^{+}$ ，所以该分解不是保持依赖分解。

对于当前的关系模式，我们先判断其是否为 BCNF：

$A \to BC$ : $A$ 不是 $R$ 的超码，违反 BCNF 条件。
$C \to D$ : $C$ 不是 $R$ 的超码，违反 BCNF 条件。

所以， $R$ 可以进行 BCNF 分解。

对于 $A \to BC$ : 分解为 $R_{3} = (A, B, C)$ 和 $R_{4} = (A, D, E)$ 我们发现 $R_{3} = R_{1}$ , $R_{4} = R_{2}$ 。

投影到 $R_{3}$ 的 FD 为： $A \to BC$ ，此时候选码是 $A$ 。
- $A \to BC$ ： $A$ 是 $R_{3}$ 的码，符合BCNF 条件。
投影到 $R_{4}$ 的 FD 为： $A \to D$ ，此时候选码是 $A E$ ， $A$ 不是其候补码，不满足 BCNF 条件，需要继续分解。

所以， $R_{1}$ 和 $R_{2}$ 的分解不是 BCNF 分解。

对于最后一个问题，是否可以找到 BCNF 分解，并保持依赖关系？我们根据第二问的判断，发现是缺失了依赖 $C \to D$ ， $C$ 在 $R_{1} (A, B, C)$ 中， $D$ 在 $R_{2} (A, D, E)$ 中。所以我们可以尝试进行其他的 BCNF 分解。

我们在前面的 BCNF 分解中，先按照 $A \to BC$ 分解。我们尝试使用 $C \to D$ 分解：

分解为 $R_{5} = (C, D)$ 和 $R_{6} = (A, C, B, E)$ 。

投影到 $R_{5}$ 的 FD 为： $C \to D$ ，此时候选码是 $C$ 。此时满足 BCNF 条件。
投影到 $R_{6}$ 的 FD 为： $A \to BC$ ，候选码是 $A E$ 。
- $A \to BC$ ： $A$ 不是 $R$ 的超码，违反 BCNF 条件，需要继续分解。

继续分解 $R_{6}$ ，分解为 $R_{7} = (A, B, C)$ 和 $R_{8} = (A, E)$ 。

投影到 $R_{7}$ 的 FD 为： $A \to BC$ ，此时候选码是 $A$ 。此时满足 BCNF 条件。
投影到 $R_{8}$ 的 FD 为： $\emptyset$ ，此时满足 BCNF 条件。

所以，该路线的最终 BCNF 分解图为：

1
    R
2
  /   \
3
CD  ACBE
4
    /  \
5
    ABC AE

$R$ 可以分解为 $R_{5} = (C, D), R_{7} = (A, B, C), R_{8} = (A, E)$

此时我们继续检查是否满足保持依赖关系：

$F_{5} = {C \to D}$
$F_{7} = {A \to BC}$
$F_{8} = \emptyset$

$(F_{5} \cup F_{7} \cup F_{8})^{+} = ({C \to D} \cup {A \to BC} \cup \emptyset)^{+} = F^{+}$

所以，即满足 BCNF 分解，并保持依赖关系的分解为： $R_{5} = (C, D), R_{7} = (A, B, C), R_{8} = (A, E)$

范式总结#

让我来总结一下：

对于 3NF 的判断方法：

1
Step 1: 找出所有候选码
2
Step 2: 逐个检查每个FD
3
  1. X是超码？ → 满足3NF
4
  2. A是部分码？ → 满足3NF
5
  3. FD 为平凡依赖？ → 满足3NF
6
  4. 都不满足？ → 违反3NF
7
Step 3: 所有FD都满足 → 关系模式是3NF

对于 BCNF 的判断方法：

1
Step 1: 找出所有候选键
2
Step 2: 对每个FD: X → Y
3
  1. X 是超码？ → 该FD满足BCNF
4
  2. FD 为平凡依赖？ → FD满足BCNF
5
  3. 都不满足 → 违反BCNF
6
Step 3: 所有FD都满足 → 关系模式是BCNF

无损连接分解判断：可以使根据定义 $R_{1} ⋈ R_{2} = R$ 且满足自然连接属性 $A$ 是候选码的一部分。或可以根据推论： $(R 1 \cap R 2) \to R 1$ 或 $(R 1 \cap R 2) \to R 2$ 在 $F^{+}$ 中，即 公共属性能决定其中一个关系的所有属性。
保持依赖分解判断：可以直接检查 $(F_{1} \cup F_{2})^{+}$ 是否等于 $F^{+}$ 。
BCNF 分解算法 - 递归分解：找到违反BCNF的依赖，分解为两个子关系，递归处理。分解结果一定满足BCNF，分解一定是无损连接，最终结果唯一性不保证（取决于选择顺序）。在选择违反BCNF的依赖时，优先选择右边属性少的（减少分裂），优先选择闭包小的（保留更多原始结构）。

事务#

事务及其特性#

事务 (Transaction) 是访问或修改数据库的一个程序执行单元，它要么全部执行，要么全部不执行。

在 SQL 语句中，使用 BEGIN TRANSACTION 开始一个事务，COMMIT 提交事务，ROLLBACK 回滚事务，END TRANSACTION 结束事务。

数据库事务具有四个主要特点，通常称为 ACID特性：

原子性（Atomicity）：事务中的所有操作 要么全部成功，要么全部失败，不会出现部分成功、部分失败的情况。
- 示例：在银行转账操作中，如果从一个账户扣款成功，但未能成功存入另一个账户，整个转账操作将被回滚，确保资金不丢失。
一致性（Consistency）：事务执行前后，数据库都处于一致 的状态，即数据库的完整性约束没有被破坏。
- 示例：在银行转账操作中，事务开始前后，所有账户的总余额应保持不变。
隔离性（Isolation）：一个事务在未提交之前，对其他事务是不可见的，多个事务并发执行时，彼此之间不会互相影响。
- 示例：在并发环境下，一个事务读取的数据不会受到其他未提交事务的影响。
持久性（Durability）：一旦事务提交，其所做的修改将 永久保存 在数据库中，即使系统崩溃也不会丢失。
- 示例：在银行转账操作中，一旦事务提交，转账结果将被永久记录，即使系统发生故障，转账结果也不会丢失。

事务在数据库中有四种基本操作（用同名变量和数据项表示）：

read_item(X): 将名为 X 的数据项读入内存，存为 X。
write_item(X): 将内存中的数据项 X 写入数据库中的数据项 X。
commit：提交事务，将所有事务操作写入数据库。
abort：放弃事务，撤销所有事务操作。

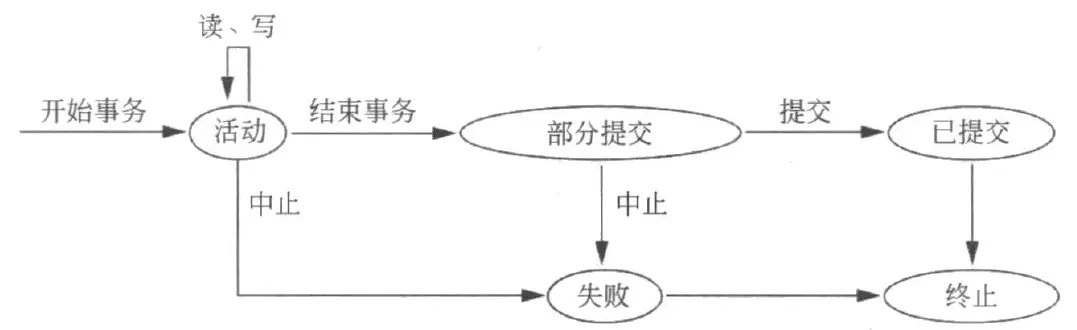
当事务 $T$ 访问数据库的所有操作都已成功执行，并且所有事务操作对数据库的影响都已记录在日志 (Log) 中时，事务 $T$ 就达到了 提交点 (Commit Point)。

事务会在日志中写入一条记录 [commit, T]，并且其会永久影响数据库中的记录。

不过，如果没有通过某个检查或者事务在其活动状态期间被中止，那么事务也可能进入失败状态 (failed state)。然后需要进行回滚操作 (Rollback) 以撤销其 WRITE 操作对数据库的影响。

下面是事务执行时的状态转换图：

调度#

调度 (Schedule): 是指一组事件的操作顺序。 $S = {T_{1}, T_{2}, ..., T_{n}}$ 。来自不同事务的操作可以在调度 $S$ 中交替执行。

例如下面两个调度，我们使用 $r, w, c, a$ 分别表示读、写、提交和放弃事务。

$S_{1}$ : $r_{1} (X); r_{2} (X); w_{1} (X); r_{1} (Y); w_{2} (X); w_{1} (Y);$
$S_{2}$ : $r_{1} (X); w_{1} (X); r_{2} (X); w_{2} (X); r_{1} (Y); a_{1};$

对于一个调度中的两个操作，它可能会出现冲突的情况。在调度中，来自不同事务的两个操作如果满足以下条件，则称为 冲突操作(Conflicting Operations)：来自不同事务的两个操作同时作用于同一数据项 (如 X)，且至少有一个是写操作。

常见的冲突情况有如下三种：

写-读冲突 (WR Conflict)：事务 $T_{i}$ 写了数据项 X，事务 $T_{j}$ 读了 X。此时事务 $T_{j}$ 读取了 $T_{i}$ 未提交的数据，称为脏读（Dirty Read）。
读-写冲突 (RW Conflict): 事务 $T_{i}$ 读了数据项 X，事务 $T_{j}$ 写了 X。此时事务 $T_{i}$ 读了 $T_{j}$ 未提交 的修改后的数据，如果之前也读过一次，则会出现数据不一致的问题，称为 不可重复读 (Non-Repeatable Read)。
写-写冲突 (WW Conflict): 事务 $T_{i}$ 写了数据项 X，事务 $T_{j}$ 也写了 X，此时事务 $T_{j}$ 重写了 $T_{i}$ 未提交的数据，称为 丢失更新（Lost Update）/ 脏写（Dirty Write）。

冲突类型	操作顺序	名称	问题
读-写冲突 (WR)	$T_{i}$ 读 `X` → $T_{j}$ 写 `X`	脏读/不可重复读	$T_{i}$ 可能读到不一致数据
写-读冲突 (RW)	$T_{i}$ 写 `X` → $T_{j}$ 读 `X`	脏读	$T_{j}$ 可能读到未提交数据
写-写冲突 (WW)	$T_{i}$ 写 `X` → $T_{j}$ 写 `X`	丢失更新/脏写	一个写操作被覆盖

可恢复调度#

对于某些调度，很容易从事务和系统失败中恢复，而对于另外一些调度，恢复过程可能相当复杂。如果按照 是否可恢复 (Recoverable) 来分类不同的调度：

不可恢复调度 (Non-recoverable Schedule): 如果事务 T2 读取了 T1 写入的数据 (T2 存在脏读)，但 T2 在 T1 提交前就提交了，这就是不可恢复调度。
可恢复调度 (Recoverable Schedule): 如果 T2 读取了 T1 写入的数据，则 T1 必须在 T2 提交前提交。这样的调度称为可恢复调度。
级联回滚调度 (Cascading Rollback Schedule): 一个事务读取了另一个未提交事务写的数据。如果写事务回滚，读事务也必须回滚。
无级联调度 (Cascadeless Schedule): 一个调度中的事务 只能读取已提交事务写入的数据。
严格调度 (Strict Schedule): 事务对数据项的读写操作都 必须等到前面对该数据项写入的事务提交或回滚后 才能进行。

例如：

不可恢复调度：如果T1后来回滚了，T2已经提交了，无法撤销！数据库进入不一致状态。

1
T1: r1(x), w1(x), ───────────, abort1
2
T2:           r2(x), commit2
3
            ↑ T2读了T1的脏数据并提交
4
                                    ↑ T1回滚（无法挽回）

可恢复调度：如果T1回滚，T2还没提交，可以一起回滚。

1
T1: r1(x), w1(x), ─────, commit1
2
T2:           r2(x), ─────────, commit2
3
            ↑ T2读了T1写的数据
4
                       ↑ T1先提交
5
                                    ↑ T2后提交

级联回滚调度：一个事务失败，引发多个事务回滚。T2读了T1写的 x（未提交），T3读了T2写的 y（未提交），T1回滚 → T2必须回滚 → T3必须回滚。

1
T1: r1(x), w1(x), ────────────────, abort1
2
T2:           r2(x), w2(y), ─────, abort2 (被迫放弃)
3
T3:                     r3(y), ───, abort3 (被迫放弃)

无级联调度：一个事务回滚不会影响其他事务。即使T2回滚，T1不受影响。

1
T1: r1(x), w1(x), commit1, ────────
2
T2:                    r2(x), w2(x), commit2
3
                       ↑ T2只读已提交的数据

严格调度：任何读和写操作都必须在事务提交或回滚后进行。

1
T1: r1(x), w1(x), commit1, ────────
2
T2:                    r2(x), w2(x), commit2
3
                       ↑ 所有操作都在T1提交后

严格调度和无级联调度的区别是：严格调度要求 读和写操作 都必须在事务提交或回滚后进行，而无级联调度则 允许写操作 在其他事务提交或回滚之前进行。

1
无级联允许：
2
r1(x), w1(x), w2(x), commit1, commit2  ← T2的写可以在T1提交前
3

4
严格调度不允许：
5
r1(x), w1(x), commit1, w2(x), commit2  ← T2的写必须等T1提交

例如如下的调度 $S_{1}, S_{2}, S_{3}$ ，如何确定它们是严格调度、无级联调度、级联回滚调度、可恢复调度还是不可恢复调度？

$S_{1}$ : $r_{1} (X); w_{1} (X); r_{2} (X); r_{1} (Y); w_{2} (X); c_{2}; c_{1};$
$S_{2}$ : $r_{1} (X); w_{1} (X); r_{2} (X); r_{1} (Y); w_{2} (X); w_{1} (Y); c_{1}; c_{2};$
$S_{3}$ : $r_{1} (X); w_{1} (X); w_{2} (X); w_{1} (Y); c_{1}; r_{2} (Y); c 2;$

我们判断这些调度时，可以遵循如下步骤：

识别 依赖关系：找出哪些操作存在读-写依赖，即 读或写同一个变量，但是在不同的事务中。
检查 提交顺序：判断是否可恢复
检查 读未提交：判断是否级联/无级联
检查 写未提交：判断是否严格

我们识别这些调度的标号，发现只有两个事务，所以我们将其改写为时间轴。

$S_{1}$ 时间轴：

1
T1: r₁(X) → w₁(X) → ─────── r₁(Y) → ────────── c₁
2
T2:            r₂(X) → ────────── w₂(X) → c₂
3
                ↑
4
          T2读了T1写的X（未提交）

$S_{2}$ 时间轴：

1
T1: r₁(X) → w₁(X) → ─────── r₁(Y) → ────── w₁(Y) → c₁
2
T2:            r₂(X) → ───────────── w₂(X) → ────── c₂
3
                ↑
4
          T2读了T1写的X（未提交）

$S_{3}$ 时间轴：

1
T1: r₁(X) → w₁(X) → ─────── w₁(Y) → c₁
2
T2:            w₂(X) → ──────────────── r₂(Y) → c₂
3
                                         ↑
4
                                   T2读了T1写的Y（已提交）

$S_{1}$ : 可以发现 $r_{2} (X)$ 依赖 $w_{1} (X)$ （T2读了T1写的 X），T2 读取了 T1 写的未提交脏数据。在调度的最后，T2 先于 T1 提交，如果 T1 回滚了，T2 无法回滚，这是 不可恢复调度。
$S_{2}$ : 可以发现 $r_{2} (X)$ 依赖 $w_{1} (X)$ （T2读了T1写的 X），T2 读取了 T1 写的未提交脏数据。在调度的最后，T1 先于 T2 提交，如果 T1 回滚了，T2 也必须回滚，这是 级联回滚调度。
$S_{3}$ : 可以发现 $r_{2} (Y)$ 依赖 $w_{1} (Y)$ （T2读了T1写的 Y），但是 T1 已提交。还可以发现一个 WW 关系： $w_{2} (X)$ 发生在 $w_{1} (X)$ 之后，此时 T2 写入了 T1 未提交的数据，这是 无级联调度。

所以： $S_{1}$ 是 不可恢复调度， $S_{2}$ 是 级联回滚调度， $S_{3}$ 是 无级联调度。

如果想要把 $S_{3}$ 改为 严格调度，只需要将 $w_{2} (X)$ 移到 $c_{1}$ 之后即可。如下 $S_{4}$ 是由 $S_{3}$ 修改而来的严格调度：

$S_{4}$ : $r_{1} (X); w_{1} (X); w_{1} (Y); c_{1}; w_{2} (X); r_{2} (Y); c_{2};$

1
T1: r₁(X) → w₁(X) → w₁(Y) → c₁
2
T2:                              w₂(X) → r₂(Y) → c₂
3
                                  ↑ 等T1提交后再写

可串行调度#

在实际情况中，我们经常会并发地运行多个事务，即进行 串行调度 (Serial Schedule): 所有事务在事务集合中按一个确定的顺序依次进行，没有交叉。

例如: T1 → T2（完全串行）

1
T1: r₁(X); w₁(X); r₁(Y); w₁(Y); c₁;
2
T2:                                  r₂(X); w₂(X); r₂(Z); w₂(Z); c₂;

但是，如果有多个事务，这样的调度效率低下。于是，我们引入 可串行化调度 (Serializable Schedule)，即：允许并发执行，但结果必须等价于某个串行调度的调度。它保证了充分利用并发，提高吞吐量，且 保证结果与串行执行一致。

相对的，我们将与任何串行调度都不等价的调度称为 不可串行化调度 (Non-Serializable Schedule)。

我们通过 结果等价 (Result Equivalence) 和 冲突等价 (Conflict Equivalence) 来定义可串行化的等价。

结果等价 (Result Equivalence): 两个调度对于相同的初始数据库状态，产生相同的最终结果。

例如：初始状态 X = 10

调度 $S_{1}$ （串行）：

1
T1: r₁(X);    X=10
2
    w₁(X=20);     ← 写X=20
3
    c₁;
4
T2:           r₂(X);    X=20
5
              w₂(X=30); ← 写X=30
6
              c₂;
7

8
最终结果：X = 30

调度 $S_{2}$ （可串行化调度）：

1
T1: r₁(X);         X=10
2
T2: r₂(X);         X=10
3
T1: w₁(X=20);          ← T1写X=20
4
T2: w₂(X=30);          ← T2写X=30（覆盖）
5
T1: c₁;
6
T2: c₂;
7

8
最终结果：X = 30

结果等价的结果相同，但 $S_{2}$ 中 T2 读的是初始值（10）， $S_{1}$ 中 T2 读的是 T1 写的值（20），它们中间状态不同，只是最终结果 碰巧相同。

冲突等价 (Conflict Equivalence): 两个调度满足以下条件则冲突等价：包含相同事务的相同操作，且 每对冲突操作的顺序相同。

我们回顾冲突操作的顺序：

冲突类型	示例	顺序重要吗？
WR	w₁(X) → r₂(X)	✅ 是
RW	r₁(X) → w₂(X)	✅ 是
WW	w₁(X) → w₂(X)	✅ 是
RR	r₁(X) → r₂(X)	❌ 否

例如：

调度 $S_{1}$ ： $r_{1} (A); w_{1} (A); r_{2} (A); r_{2} (B); w_{2} (B); r_{1} (B); w_{1} (B);$
调度 $S_{2}$ ： $r_{1} (A); w_{1} (A); r_{1} (B); w_{1} (B); r_{2} (A); r_{2} (B); w_{2} (B);$

我们可以分析其冲突对：

$S_{1}$ 冲突对：
1. $w_{1} (A) \to r_{2} (A)$ ：WR冲突
2. $w_{1} (B) \to w_{2} (B)$ ：WW冲突
3. $r_{2} (B) \to w_{1} (B)$ ：RW冲突
$S_{2}$ 冲突对：
1. $w_{1} (A) \to r_{2} (A)$ ：WR冲突
2. $w_{1} (B) \to w_{2} (B)$ ：WW冲突
3. $r_{1} (B) \to w_{2} (B)$ ：RW冲突

我们可以发现 $S_{1}$ 和 $S_{2}$ 在第三对冲突对中的顺序不一样，所以认为 $S_{1}$ 和 $S_{2}$ 不是冲突等价。

有了冲突等价，我们可以得到一种基于冲突等价的可串行化调度：如果一个调度 $S$ 是 冲突可串行化 (Conflict Serializability) 的，当且仅当它与某个串行调度 冲突等价。

例如，

$S_{3}$ ： $w_{1} (A); r_{2} (B); r_{1} (B); r_{2} (A);$
$S_{4}$ ： $w_{1} (A); r_{1} (B); r_{2} (B); r_{2} (A);$

我们分析其冲突对：

$S_{3}$ 冲突对： $w_{1} (A) \to r_{2} (A)$ ：WR冲突
$S_{4}$ 冲突对： $w_{1} (A) \to r_{2} (A)$ ：WR冲突

此时， $S_{3}$ 和 $S_{4}$ 是冲突等价的，因为 $S_{4}$ 是串行调度，所以 $S_{3}$ 是冲突可串行化的。

判断调度是否是冲突可串行化时，我们一般使用 优先图 (Precedence Graph) 测试法。

我们有如下定义：一个优先图 $G = (V, E)$ 是一个有向图，其 顶点集为事务集合，边集为事务之间的冲突关系。

节点 (V)：每个事务一个节点
边 (E)：如果存在冲突操作 $o p_{i} (X) \to o p_{j} (X)$ ，则画边 $T_{i} \to T_{j}$

若调度 $S$ 的优先图 $G$ 是无环的 (Acyclic)，则 $S$ 是 冲突可串行化 (Conflict Serializable) 的。

构造优先图的步骤很简单：

列出所有事务 (V)：根据下标，列出所有参与调度的事务。
列出所有冲突关系 (E)：根据冲突对，列出所有冲突关系。
根据步骤 1 和 2 构造优先图 $G$ ，检查优先图 $G$ 是否无环。
如果无环，则调度 $S$ 是冲突可串行化的。如果存在环，则调度 $S$ 不是冲突可串行化的。

下面是一些例子：

对于： $S_{3}$ ： $w_{1} (A); r_{2} (B); r_{1} (B); r_{2} (A);$ ，画出其优先图。

列出所有事务： $T_{1}, T_{2}$ 。
列出所有冲突关系： $w_{1} (A) \to r_{2} (A)$
构造优先图 $G = (V, E)$ ： $T_{1} \to T_{2}$ ，它显然没有环，所以 $S_{3}$ 是冲突可串行化的。

对于： $S_{5}$ ： $w_{1} (a); r_{3} (a); r_{1} (b); w_{2} (b); w_{3} (c); r_{4} (c); w_{2} (d); r_{4} (d);$ ，画出其优先图。

列出所有事务： $T 1, T 2, T 3, T 4$ 。
列出所有冲突关系：注意只找同一个数据的。
1. WR: $w_{1} (a); \to r_{3} (a);$ $T 1 \to T 3$
2. RW: $r_{1} (b); \to w_{2} (b);$ $T 1 \to T 2$
3. WR: $w_{3} (c); \to r_{4} (c);$ $T 3 \to T 4$
4. WR: $w_{2} (d); \to r_{4} (d);$ $T 2 \to T 4$
构造优先图 $G = (V, E)$ ：

1
G:
2
  T1
3
 /  \
4
T2  T3
5
 \  /
6
  T4

检查优先图 $G$ 是否无环。很明显，存在一个环 $T 1 \to T 3 \to T 4 \to T 2 \to T 1$ 或 $T 1 \to T 2 \to T 4 \to T 3 \to T 1$ ，所以 $S_{5}$ 不是冲突可串行化的。

事务例题和总结#

事务例题#

事务这一章主要要求我们识别和判断不同的调度类型。

按照可恢复调度分类有：不可恢复调度、可恢复调度、级联回滚调度、无级联调度和严格调度。

按可串行化分类有：不可串行化、冲突可串行化。

有这样的调度 $S = w_{2} (b); r_{1} (a); w_{1} (a); r_{2} (a); c 1; c 2;$ . 请你判断该调度在按照可恢复调度分类和可串行化分类下，分别属于哪类调度。

对于这样的问题，我们依然找出其冲突对： $w_{1} (a); \to r_{2} (a);$ ，这是一个 WR 冲突。

按可串行化分类，如果 $S$ 是 可串行化 的，则 $S$ 的优先图 $G$ 是无环的。

构造优先图 $G = (V, E)$ ： $T 1 \to T 2$ ，很明显无环。所以 $S$ 是 冲突可串行化 的。

按可恢复调度分类，我们发现：发生这个冲突会导致：T2 读取 T1 未提交的数据，如果 T1 回滚，T2 也必须回滚，所以这是一个 级联回滚调度。注意：因为 T1 先于 T2 提交，所以 $S$ 依然是 可恢复 的，只是不是 无级联回滚 的。

如果想要将 $S$ 改为无级联回滚的，则需要解决冲突对 $w_{1} (a); \to r_{2} (a);$ 。所以一个简单的解决方案是在 T2 读之前先提交 T1。

$S_{2}$ : $w_{2} (b); r_{1} (a); w_{1} (a); c 1; r_{2} (a); c 2;$

对于一个调度 $S = r_{3} (Z); w_{3} (Z); r_{1} (X); r_{2} (Y); w_{2} (Y); w_{1} (X); r_{1} (Y); r_{3} (X); c 1; c 2; c 3;$ ，判断它是否是可串行化的，是否可恢复，是否是无级联回滚的。

同样，我们分析其冲突对，因为这个调度较长，我们可以将其改写为时间轴的方式容易发现冲突对：

1
T1:                r1(X) →             w1(X) → r1(Y) →   c1
2
T2:                       r2(Y) → w2(Y) →                  c2
3
T3: r3(Z) → w3(Z) →                                 r3(X) →  c3

可以发现：

$w_{1} (X); \to r_{3} (X);$ : WR 冲突
$w_{2} (Y); \to r_{1} (Y);$ : WR 冲突

对于可串行化，我们可以构造优先图 $G = (V, E)$ ：节点有 $T 1, T 2, T 3$ ，边有 $T 1 \to T 3, T 2 \to T 1$ 。

1
T1 → T3
2
↑
3
T2

构造优先图 $G$ 无环，所以 $S$ 是冲突可串行化的。

对于可恢复调度，要求如果 $T_{j}$ 读取了 $T_{i}$ 写入的数据，则 $T_{i}$ 必须在 $T_{j}$ 提交前提交。在该题中则要求提交顺序为： $T 2, T 1, T 3$ 。

因为 $S$ 的提交顺序为 $T 1, T 2, T 3$ ，所以 $S$ 是 不可恢复 的。

此外，因为 T3 读取了 T1 未提交的数据，T1 读取了 T2 未提交的数据，当 T2 回滚时，T1和T3 也必须回滚。所以 $S$ 是 级联回滚 的。

若要把 $S$ 改为可恢复的调度，则需要调整提交顺序。 $S_{2} = r_{3} (Z); w_{3} (Z); r_{1} (X); r_{2} (Y); w_{2} (Y); w_{1} (X); r_{1} (Y); r_{3} (X); c 2; c 1; c 3;$

若要把 $S$ 改为无级联回滚的调度，则需要在读取前提交。 $S_{3} = r_{3} (Z); w_{3} (Z); r_{1} (X); r_{2} (Y); w_{2} (Y); c 2; w_{1} (X); r_{1} (Y); c 1; r_{3} (X); c 3;$

事务总结#

总结一下事务的例题和常见考法：

首先最重要的是：找出冲突对。

冲突类型	模式	优先图边	含义
WR	wᵢ(X) → rⱼ(X)	Tᵢ → Tⱼ	j读了i写的值
RW	rᵢ(X) → wⱼ(X)	Tᵢ → Tⱼ	j覆盖了i读的值
WW	wᵢ(X) → wⱼ(X)	Tᵢ → Tⱼ	j覆盖了i写的值

冲突对找出后，就可以构造优先图 $G = (V, E)$ ，并检查 $G$ 是否无环。

若 $G$ 无环，则 $S$ 是 冲突可串行化 的。

对于可恢复性的判断：根据冲突对去检查提交顺序。因为其要求读取其他事务写的数据前提交，它决定的是最后提交的顺序，没有要求一定要读取前提交。所以只需要找 读了谁，谁先提交 即可判断。

对于无级联回滚的判断：在可恢复的基础上，更加强硬的要求另一个事务的提交顺序必须在读取之前。所以只需要找 读之前，必提交 即可判断。

而对于最为严格的严格调度，在无级联回滚的基础上，还要求不能出现同写一个数据块，且未提交的操作。所以需要找 写之后，必提交 即可判断。

这些调度的关系如下：严格调度 ⊂ 无级联回滚 ⊂ 可恢复 ⊂ 可串行化 ⊂ 所有调度

1
┌─────────────────────────────────┐
2
│ Step 0: 预处理                  │
3
│ - 给操作编号                     │
4
│ - 识别事务和数据项               │
5
└─────────────────────────────────┘
6
              ↓
7
┌─────────────────────────────────┐
8
│ Step 1: 判断可串行化            │
9
│ ├─ 找冲突对                     │
10
│ ├─ 画优先图                     │
11
│ ├─ 检测环                       │
12
│ └─ 输出结果                     │
13
└─────────────────────────────────┘
14
              ↓
15
┌─────────────────────────────────┐
16
│ Step 2: 判断可恢复              │
17
│ ├─ 找读依赖                     │
18
│ ├─ 检查提交顺序                 │
19
│ └─ 输出结果                     │
20
└─────────────────────────────────┘
21
              ↓
22
┌─────────────────────────────────┐
23
│ Step 3: 判断无级联              │
24
│ ├─ 检查每个读操作               │
25
│ ├─ 判断写者是否已提交           │
26
│ └─ 输出结果                     │
27
└─────────────────────────────────┘