本章将从数据挖掘中的四项经典核心任务开始,探索数据挖掘的底层逻辑。从寻找相似性的 TF-IDF 和 MinHash 开始,到 Clustering (聚类) 和 Anomaly Detection (识别异常),最后再通过隐变量模型 (Latent Variable Model) 剥离表象,直达隐变量。
本章将通过四个经典的例题,并补充必要的数学知识,来介绍数据挖掘中的四项核心任务。
注:常见的考试中会出的部分将使用 红色 进行标记。简略部分的总结请看 总结部分
Task 1: 基础数据收集与相似度分析# 这一部分主要涉及数据的预处理,计算 TF-IDF ,文档的向量化和简单的相似度计算。文档相似度分析是整个自然语言处理(NLP)和信息检索的核心基石。
这个过程包括:预处理与词频统计 -> TF-IDF 计算 -> 向量化构建 -> 余弦相似度分析。
假设我们有以下四个文档:
Document 1 : The Development of Electric Vehicles
Electric vehicles have rapidly evolved, with battery technology driving their growth: new high-capacity battery designs have doubled the range of electric vehicles, directly elevating their performance. Better performance has made electric vehicles more competitive than traditional vehicles, attracting wider adoption. As battery innovation continues, electric vehicles will further improve in performance, solidifying their role in sustainable transportation.
Document 2 : Advancements in Battery Technology
Modern battery innovations are reshaping global energy systems. New lithium-ion variants boost energy density, letting a single battery store more charge and extend device lifespans. Smart charge management also optimizes battery performance, reducing waste and enhancing storage efficiency. As demand for clean energy grows, next-gen batteries will further bridge gaps between energy production and storage, making reliable, fast charge solutions universal.
Document 3 : Renewable Energy Integration
Renewable energy integration has become a global priority, as societies strive to replace fossil fuels with sustainable renewable sources like solar and wind. A key challenge lies in storing excess renewable energy, and battery technology emerges as a critical solution: batteries store surplus energy during peak production and release it when demand surges. Without reliable battery storage, the instability of renewable energy would hinder its large-scale integration into power grids, making batteries indispensable for unlocking renewable energy’s full potential.
Document 4 : Sustainable Transportation Solutions
Sustainable transportation solutions are reshaping urban mobility, with electric vehicles at their core. These electric vehicles reduce carbon emissions far more effectively than traditional cars, aligning perfectly with sustainable goals. Cities worldwide now prioritize electric transportation infrastructure—charging stations, dedicated lanes—to boost adoption of electric vehicles. Only by scaling such sustainable measures can transportation systems break free from fossil fuel reliance, making electric vehicles a cornerstone of truly sustainable transportation.
Step 1 第一步:数据预处理与关键词提取 (Pre-processing)
在分析文档相似度之前,我们必须先清理数据。
去除停用词 (Stop Words) : 原始文档包含很多像 “the”, “is”, “and” 这样的功能词,它们对文本含义贡献很小。我们需要根据给定的列表移除它们。提取关键词 (Key Term Extraction) : 去除停用词后,我们要统计剩余词汇的频率,并确定一个包含 K K K V V V V = { battery, electric, vehicles, energy, sustainable, transportation, performance, storage, charge, renewable } V = \{\text{battery, electric, vehicles, energy, sustainable, transportation, performance, storage, charge, renewable}\} V = { battery, electric, vehicles, energy, sustainable, transportation, performance, storage, charge, renewable }
词频统计 (Count) :接下来在每个文档中,计算每个关键词出现的原始次数。在考试中,词频需要根据文档进行补全计数。此外,我们最好还需要计算出每个文档涉及的 关键词总数 。 D 1 : battery:3, electric:5, vehicles:6, energy:0, sustainable:1, transportation:1, performance:4,storage:0, charge:0, renewable:0 D1: \text{battery:3, electric:5, vehicles:6, energy:0, sustainable:1, transportation:1, performance:4,storage:0, charge:0, renewable:0} D 1 : battery:3, electric:5, vehicles:6, energy:0, sustainable:1, transportation:1, performance:4,storage:0, charge:0, renewable:0
D1 关键词总数为 3 + 5 + 6 + 0 + 1 + 1 + 4 + 0 + 0 + 0 = 20 3+5+6+0+1+1+4+0+0+0 = 20 3 + 5 + 6 + 0 + 1 + 1 + 4 + 0 + 0 + 0 = 20
D 2 : battery:4, electric:0, vehicles:0, energy:5, sustainable:0, transportation:0, performance:1,storage:2, charge:3, renewable:0 D2: \text{battery:4, electric:0, vehicles:0, energy:5, sustainable:0, transportation:0, performance:1,storage:2, charge:3, renewable:0} D 2 : battery:4, electric:0, vehicles:0, energy:5, sustainable:0, transportation:0, performance:1,storage:2, charge:3, renewable:0
D2 关键词总数为 4 + 0 + 0 + 5 + 0 + 0 + 1 + 2 + 3 + 0 = 15 4+0+0+5+0+0+1+2+3+0 = 15 4 + 0 + 0 + 5 + 0 + 0 + 1 + 2 + 3 + 0 = 15
D 3 : attery:4, electric:0, vehicles:0, energy:8, sustainable:1, transportation:0, performance:0,storage:1, charge:0, renewable:5 D3: \text{attery:4, electric:0, vehicles:0, energy:8, sustainable:1, transportation:0, performance:0,storage:1, charge:0, renewable:5} D 3 : attery:4, electric:0, vehicles:0, energy:8, sustainable:1, transportation:0, performance:0,storage:1, charge:0, renewable:5
D3 关键词总数为 4 + 0 + 0 + 8 + 1 + 0 + 0 + 1 + 0 + 5 = 19 4+0+0+8+1+0+0+1+0+5 = 19 4 + 0 + 0 + 8 + 1 + 0 + 0 + 1 + 0 + 5 = 19
D 4 : battery:0, electric:5, vehicles:5, energy:0, sustainable:4, transportation:4, performance:0,storage:0, charge:0, renewable:0 D4: \text{battery:0, electric:5, vehicles:5, energy:0, sustainable:4, transportation:4, performance:0,storage:0, charge:0, renewable:0} D 4 : battery:0, electric:5, vehicles:5, energy:0, sustainable:4, transportation:4, performance:0,storage:0, charge:0, renewable:0
D4 关键词总数为 0 + 5 + 5 + 0 + 4 + 4 + 0 + 0 + 0 + 0 = 18 0+5+5+0+4+4+0+0+0+0 = 18 0 + 5 + 5 + 0 + 4 + 4 + 0 + 0 + 0 + 0 = 18
Step 2 第二步:TF-IDF 计算 (The Core Calculation)
TF-IDF 是一种统计方法,用于衡量一个词对于一个文档集中的某一篇文档的重要性。它的计算包含:1. 词频 (Term Frequency, TF) 和 逆文档频率 (Inverse Document Frequency, IDF)。在考试中,TF-IDF 一般需要根据具体的数据和给出的 log 参考值进行计算 (TF为0的值不需要计算) 。
TF (Term Frequency, 词频) : 衡量词 t t t d d d
T F ( t , d ) = 词 t 在文档 d 中的次数 文档 d 的总词数 TF(t,d) = \frac{\text{词 t 在文档 d 中的次数}}{\text{文档 d 的总词数}} TF ( t , d ) = 文档 d 的总词数 词 t 在文档 d 中的次数 例如:D1 中的 electric 出现次数为 5 5 5 20 20 20
T F ( electric , D 1 ) = 5 20 = 0.25 TF(\text{electric}, D1) = \frac{5}{20} = 0.25 TF ( electric , D 1 ) = 20 5 = 0.25
IDF (Inverse Document Frequency, 逆文档频率) : 衡量词 t t t log \log log ln \ln ln 以 e e e ),以方便计算。
I D F ( t ) = log ( N D F ( t ) ) IDF(t) = \log(\frac{N}{DF(t)}) I D F ( t ) = log ( D F ( t ) N ) 其中 N N N N = 4 N=4 N = 4 D F ( t ) DF(t) D F ( t ) t t t
例如对于词 electric ,它出现在 D1 和 D4 中,所以 D F = 2 DF=2 D F = 2
I D F ( electric ) = log ( 4 2 ) = 0.6931 IDF(\text{electric}) = \log(\frac{4}{2}) = 0.6931 I D F ( electric ) = log ( 2 4 ) = 0.6931 对于词 charge ,只出现在 D2 中,D F = 1 DF=1 D F = 1
I D F ( charge ) = log ( 4 1 ) = 1.3863 IDF(\text{charge}) = \log(\frac{4}{1}) = 1.3863 I D F ( charge ) = log ( 1 4 ) = 1.3863
TF-IDF : 词频-逆文档频率的乘积,用于衡量一个词对于一个文档的权重。
T F − I D F = T F × I D F TF-IDF = TF \times IDF TF − I D F = TF × I D F 例如 D1 中 electric 的 TF-IDF 为:
TF-IDF = 0.25 × 0.6931 = 0.173275 \text{TF-IDF} = 0.25 \times 0.6931 = 0.173275 TF-IDF = 0.25 × 0.6931 = 0.173275
Step 3 第三步:文档向量化 (Vectorization)
计算出所有 TF-IDF 值后,我们将每篇文档转换成一个向量。这是将文本转化为计算机可计算形式的关键步骤。
我们需要构建一个矩阵,行代表文档 ,列代表词汇表中 的 K K K 关键词 。这样的表示方式称为 词袋模型 (Bag-of-Words model) 。
在考试中,向量化需要根据之前计算得到的 TF-IDF 值进行填空即可。
D 1 : [0.043, 0.173, 0.208, 0, 0.014, 0.035, 0.139, 0, 0, 0] D 2 : [0.077, 0, 0, 0.231, 0, 0, 0.046, 0.092, 0.277, 0] D 3 : [0.061, 0, 0, 0.292, 0.015, 0, 0, 0.037, 0, 0.365] D 4 : [0, 0.193, 0.193, 0, 0.064, 0.154, 0, 0, 0, 0] \begin{align*}
D1&: \text{[0.043, 0.173, 0.208, 0, 0.014, 0.035, 0.139, 0, 0, 0]} \\
D2&: \text{[0.077, 0, 0, 0.231, 0, 0, 0.046, 0.092, 0.277, 0]} \\
D3&: \text{[0.061, 0, 0, 0.292, 0.015, 0, 0, 0.037, 0, 0.365]} \\
D4&: \text{[0, 0.193, 0.193, 0, 0.064, 0.154, 0, 0, 0, 0]}
\end{align*}
D 1 D 2 D 3 D 4 : [0.043, 0.173, 0.208, 0, 0.014, 0.035, 0.139, 0, 0, 0] : [0.077, 0, 0, 0.231, 0, 0, 0.046, 0.092, 0.277, 0] : [0.061, 0, 0, 0.292, 0.015, 0, 0, 0.037, 0, 0.365] : [0, 0.193, 0.193, 0, 0.064, 0.154, 0, 0, 0, 0] 向量中为 0 的位置表示该词(如 energy, storage)在该文档中未出现。
Step 4 第四步:余弦相似度分析 (Cosine Similarity)
最后,我们通过计算向量之间的夹角余弦值来判断文档有多相似。值越接近 1 1 1 cos ( θ ) = A ⋅ B ∥ A ∥ ∥ B ∥ \cos(\theta) = \frac{A \cdot B}{\|A\| \|B\|} cos ( θ ) = ∥ A ∥∥ B ∥ A ⋅ B
计算向量长度 (Magnitude/Norm) : 首先计算每个向量的模长 ∣ ∣ D ∣ ∣ ||D|| ∣∣ D ∣∣ 0.043 2 + 0.173 2 + . . . ≈ 0.309 \sqrt{0.043^2 + 0.173^2 + ...} \approx 0.309 0.04 3 2 + 0.17 3 2 + ... ≈ 0.309
计算点积 (Dot Product) : 计算两个向量 对应位置数值的乘积 之和。这个就是矩阵的点乘,以 D1 和 D4 为例:
D 1 ⋅ D 4 = ( 0.173 × 0.193 ) + ( 0.208 × 0.193 ) + . . . ≈ 0.079819 D1 \cdot D4 = (0.173 \times 0.193) + (0.208 \times 0.193) + ... \approx 0.079819 D 1 ⋅ D 4 = ( 0.173 × 0.193 ) + ( 0.208 × 0.193 ) + ... ≈ 0.079819
计算相似度 :
S i m ( D 1 , D 4 ) = D 1 ⋅ D 4 ∣ ∣ D 1 ∣ ∣ × ∣ ∣ D 4 ∣ ∣ = 0.079819 0.309 × 0.320 ≈ 0.807 Sim(D1, D4) = \frac{D1 \cdot D4}{||D1|| \times ||D4||} = \frac{0.079819}{0.309 \times 0.320} \approx 0.807 S im ( D 1 , D 4 ) = ∣∣ D 1∣∣ × ∣∣ D 4∣∣ D 1 ⋅ D 4 = 0.309 × 0.320 0.079819 ≈ 0.807
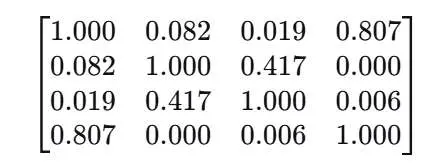
现在可以得到最终的相似度矩阵:
通过这样的矩阵,可以得出文档之间的相似度关系结论:
D1 与 D4 最相似(≈0.806):共同高权重词是 electric / vehicles / sustainable / transportation(D4 几乎围绕可持续交通与电动车)。
D2 与 D3 次相似(≈0.416):共同点在 energy / battery / storage(电池与能源存储链条)。
D2 与 D4 几乎完全不相似(0):两者在该词汇表 TF‑IDF 上没有共同非零维度(D2 偏 energy/charge/storage;D4 偏 electric/transportation)。
在考试中,余弦相似度需要进行部分计算,并根据得到的相似度矩阵给出结论。
总结:这一部分是一个完整的文本相似度计算过程,需要根据具体数据进行计算和填空。建议是多加练习计算这一过程,并使用实际数据进行测试。
Task 2: MinHash (最小哈希)# 如果在 Task 1 中我们关注的是词频和精确的余弦相似度,那么在 Task 2 中,我们切换到了 处理大规模数据 的思维模式:我们不再关心词频,只关心“有没有 ”,并用极短的 签名 (Signatures) 来快速估算文档的相似度。
Minhash 通过随机哈希函数,将文档映射到一个 签名 (Signature) 中,然后计算签名之间的相似度。
Step 1 第一步:理解数据表示 (One-Hot Encoding)
首先,文档将不再转换为词频向量,而是简单的 二进制向量 (Binary Vectors)。
1 1 1 0 0 0 例如给出关键词列表:
Keywords: [algorithm, data, learning, neural, network, optimization, pattern, recognition, system, training] \text{Keywords: [algorithm, data, learning, neural, network, optimization, pattern, recognition, system, training]} Keywords: [algorithm, data, learning, neural, network, optimization, pattern, recognition, system, training] 我们可以得到对应的每个文档的二进制向量(文档的具体内容省略了,这里直接展示了二进制向量):
D 1 [ 1 , 1 , 1 , 0 , 0 , 1 , 0 , 0 , 1 , 0 ] D1[1, 1, 1, 0, 0, 1, 0, 0, 1, 0] D 1 [ 1 , 1 , 1 , 0 , 0 , 1 , 0 , 0 , 1 , 0 ] D 2 [ 1 , 1 , 0 , 1 , 1 , 0 , 1 , 1 , 0 , 1 ] D2[1, 1, 0, 1, 1, 0, 1, 1, 0, 1] D 2 [ 1 , 1 , 0 , 1 , 1 , 0 , 1 , 1 , 0 , 1 ] D 3 [ 0 , 1 , 1 , 0 , 0 , 1 , 0 , 0 , 1 , 1 ] D3[0, 1, 1, 0, 0, 1, 0, 0, 1, 1] D 3 [ 0 , 1 , 1 , 0 , 0 , 1 , 0 , 0 , 1 , 1 ] D 4 [ 1 , 0 , 0 , 1 , 1 , 0 , 1 , 1 , 0 , 0 ] D4[1, 0, 0, 1, 1, 0, 1, 1, 0, 0] D 4 [ 1 , 0 , 0 , 1 , 1 , 0 , 1 , 1 , 0 , 0 ] 对于 D1,它的向量中的 1 1 1
Step 2 第二步:MinHash 签名计算
MinHash 的核心思想是:置换 (Permutation) ,即打乱列的顺序,看谁先出现 “1”。
我们需要根据置换向量 P P P 找到每个文档第一个出现 1 的位置 ,这个位置就是 MinHash 签名 (Signature) 。在考试中,会给出随机的置换向量,根据向量的检查顺序找到其第一个 “1” 出现的位置。并得到 Document / MinHash Signature 表。
例如两个随机置换顺序 P 1 P1 P 1 P 2 P2 P 2
P 1 : [ 3 , 8 , 1 , 6 , 10 , 4 , 9 , 2 , 7 , 5 ] P1: [3, 8, 1, 6, 10, 4, 9, 2, 7, 5] P 1 : [ 3 , 8 , 1 , 6 , 10 , 4 , 9 , 2 , 7 , 5 ] 这意味着:先检查第 3 列,再检查第 8 列,然后第 1 列…以此类推。
P 2 : [ 7 , 2 , 9 , 5 , 3 , 10 , 1 , 4 , 6 , 8 ] P2: [7, 2, 9, 5, 3, 10, 1, 4, 6, 8] P 2 : [ 7 , 2 , 9 , 5 , 3 , 10 , 1 , 4 , 6 , 8 ] 同理,P 2 P2 P 2
我们需要记录的是在新的检查顺序下 ,第几次检查遇到了 “1” (即 Rank/Index),而不是原始的列号。
例如对于置换 1 (P 1 P1 P 1
D 1 ′ [ 1 , 0 , 1 , 1 , 0 , 0 , 1 , 1 , 0 , 0 ] D1'[1, 0, 1, 1, 0, 0, 1, 1, 0, 0] D 1 ′ [ 1 , 0 , 1 , 1 , 0 , 0 , 1 , 1 , 0 , 0 ] D 2 ′ [ 0 , 1 , 1 , 0 , 1 , 1 , 0 , 1 , 1 , 1 ] D2'[0, 1, 1, 0, 1, 1, 0, 1, 1, 1] D 2 ′ [ 0 , 1 , 1 , 0 , 1 , 1 , 0 , 1 , 1 , 1 ] D 3 ′ [ 1 , 0 , 0 , 1 , 1 , 0 , 1 , 1 , 0 , 0 ] D3'[1, 0, 0, 1, 1, 0, 1, 1, 0, 0] D 3 ′ [ 1 , 0 , 0 , 1 , 1 , 0 , 1 , 1 , 0 , 0 ] D 4 ′ [ 0 , 1 , 1 , 0 , 0 , 1 , 0 , 0 , 1 , 1 ] D4'[0, 1, 1, 0, 0, 1, 0, 0, 1, 1] D 4 ′ [ 0 , 1 , 1 , 0 , 0 , 1 , 0 , 0 , 1 , 1 ] 我们按照 P 1 P1 P 1
D1: 第一个”1”的索引是 1,所以 h 1 ( D 1 ) = 1 h_1(D1) = 1 h 1 ( D 1 ) = 1 h 1 ( D 2 ) = 2 h_1(D2) = 2 h 1 ( D 2 ) = 2 h 1 ( D 3 ) = 1 h_1(D3) = 1 h 1 ( D 3 ) = 1 h 1 ( D 4 ) = 2 h_1(D4) = 2 h 1 ( D 4 ) = 2
同理,我们可以得到 h 2 ( D 1 ) = 2 h_2(D1)=2 h 2 ( D 1 ) = 2 h 2 ( D 2 ) = 1 h_2(D2)=1 h 2 ( D 2 ) = 1 h 2 ( D 3 ) = 2 h_2(D3)=2 h 2 ( D 3 ) = 2 h 2 ( D 4 ) = 1 h_2(D4)=1 h 2 ( D 4 ) = 1
所以,此时有:
Document MinHash Signature [h 1 , h 2 h_1, h_2 h 1 , h 2 D1 [1, 2] D2 [2, 1] D3 [1, 2] D4 [2, 1]
Step 3 第三步:相似度对比 (Jaccard vs. MinHash)
最后一步是计算 MinHash 的文档相似度,并评估 MinHash 的效果。
MinHash 方法中文档的相似度通过计算两两签名向量中,数值相同的位置所占的比例,即 数值相同的位置个数 / 所有的位置数 。在考试中,可能会有多个签名,需要逐一进行比较计算其相似度。有几个置换向量就有几个位置数。
例如:
D1 和 D3,D 1 = [ 1 , 2 ] , D 3 = [ 1 , 2 ] D1=[1, 2], D3=[1, 2] D 1 = [ 1 , 2 ] , D 3 = [ 1 , 2 ] 1 = 1 , 2 = 2 1=1, 2=2 1 = 1 , 2 = 2 S i m ( D 1 , D 3 ) = 2 2 = 1 Sim(D1, D3) = \frac{2}{2} = 1 S im ( D 1 , D 3 ) = 2 2 = 1
D1 和 D2,D 1 = [ 1 , 2 ] , D 2 = [ 2 , 1 ] D1=[1, 2], D2=[2, 1] D 1 = [ 1 , 2 ] , D 2 = [ 2 , 1 ] S i m ( D 1 , D 2 ) = 0 / 2 = 0 Sim(D1, D2) = 0/2 = 0 S im ( D 1 , D 2 ) = 0/2 = 0
因为 MinHash 是用“哈希碰撞”的概率来模拟“集合重合”的比例。我们需要比较其相似度和真实值的差距。真实的相似度一般使用 Jaccard 相似度 来计算。它实际是文档关键词的 交集大小 / 并集大小 。
J ( A , B ) = ∣ A ∩ B ∣ ∣ A ∪ B ∣ J(A, B) = \frac{|A \cap B|}{|A \cup B|} J ( A , B ) = ∣ A ∪ B ∣ ∣ A ∩ B ∣ 例如 D1 和 D3,有 4 个共同关键词:“data, learning, optimization, system”,一共有 6 个非重复的关键词:“algorithm, data, learning, optimization, system, training”。
所以 J ( D 1 , D 3 ) = 4 / 6 = 0.667 J(D1, D3) = 4/6 = 0.667 J ( D 1 , D 3 ) = 4/6 = 0.667
我们可以将 MinHash 的相似度与 Jaccard 的相似度进行对比,并评估 MinHash 的效果。即计算其误差 E = ∣ S i m ( A , B ) − J ( A , B ) ∣ E = |Sim(A, B) - J(A, B)| E = ∣ S im ( A , B ) − J ( A , B ) ∣
例如 D1 和 D3,E = ∣ 1 − 0.667 ∣ = 0.333 E = |1 - 0.667| = 0.333 E = ∣1 − 0.667∣ = 0.333 P 1 , P 2 P1, P2 P 1 , P 2
MinHash 是无偏估计。随着置换次数(哈希函数数量)的增加 ,MinHash 相似度会逐渐收敛于真实的 Jaccard 相似度 。
总结:在计算 MinHash 的签名时,需要记录文档向量中第一个出现的 1 的索引 。
列出置换顺序:把 P P P
逐个核对文档向量:像扫雷一样,按照 P P P
填表:签名矩阵的行是哈希函数(P1, P2…),列是文档(D1, D2…)。
注意题目给出的索引是从 0 开始还是从 1 开始。如果 P 1 P1 P 1
Task 3: 聚类分析与异常检测# 这一部分分为两个核心阶段:K-means 聚类迭代 和 基于统计的异常检测 。
聚类 (Clustering) :寻找“大多数”的共性,建立秩序。异常检测 (Anomaly Detection) :关注“极少数”的偏离,发现变数。 Part 1 第一阶段:K-means 聚类 (K-means Clustering)
K-means 的目标是找到数据的 自然分组 。例如,把 6 个点分成 K = 2 K=2 K = 2
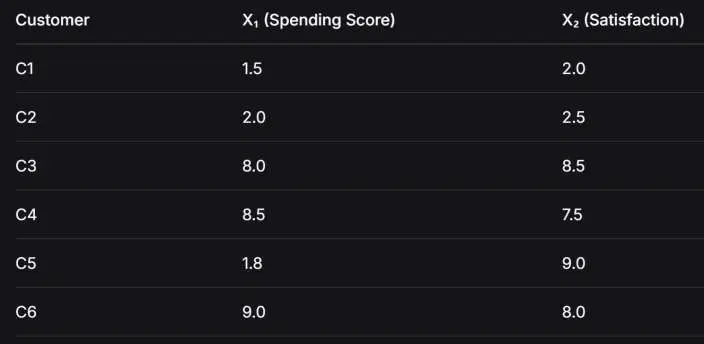
假设我们有 6 个客户,两个特征 X 1 X_1 X 1 X 2 X_2 X 2 C 1 ( 1.5 , 2.0 ) C_1(1.5, 2.0) C 1 ( 1.5 , 2.0 ) C 2 ( 8.0 , 8.5 ) C_2(8.0, 8.5) C 2 ( 8.0 , 8.5 )
在考试中,经常需要补全迭代过程中的一些数据,需要牢记这个过程。
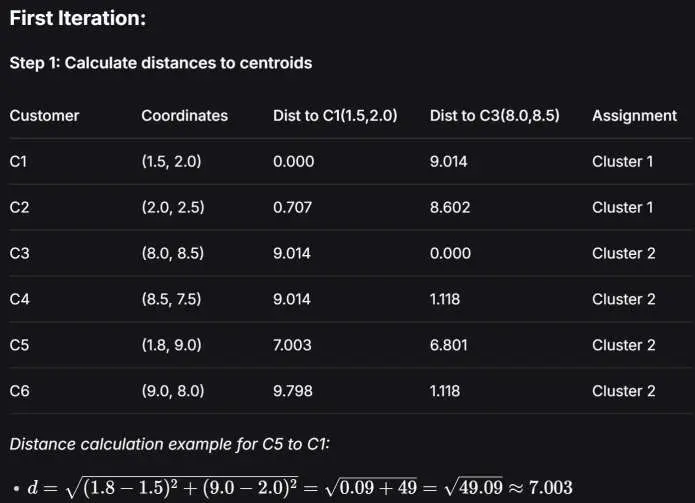
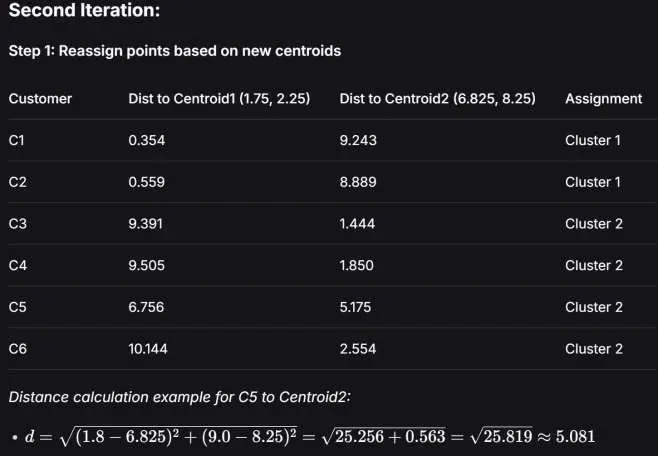
第一次迭代 —— 指派 (Assignment) :计算每个点到这两个中心的欧几里得距离,谁近就归谁。
d = ( x 1 − c 1 ) 2 + ( x 2 − c 2 ) 2 d = \sqrt{(x_1-c_1)^2 + (x_2-c_2)^2} d = ( x 1 − c 1 ) 2 + ( x 2 − c 2 ) 2 例如 C 5 ( 1.8 , 9.0 ) C5(1.8, 9.0) C 5 ( 1.8 , 9.0 ) ≈ 7.003 \approx 7.003 ≈ 7.003 ≈ 6.801 \approx 6.801 ≈ 6.801 6.801 < 7.003 6.801 < 7.003 6.801 < 7.003 簇 2 。
最后得到:
簇 1: C1, C2
簇 2: C3, C4, C5, C6
计算误差 MSE (Mean Squared Error,均方差/标准差) :根据给出的 MSE 公式,计算当前迭代中的均方误差。
M S E = 1 N ∑ i = 1 N ∣ ∣ x i − μ c ( i ) ∣ ∣ 2 MSE = \frac{1}{N} \sum_{i=1}^{N} ||x_i - \mu_{c(i)}||^2 MSE = N 1 i = 1 ∑ N ∣∣ x i − μ c ( i ) ∣ ∣ 2 其中 N N N N = 6 N=6 N = 6 x i x_i x i i i i μ c ( i ) \mu_{c(i)} μ c ( i ) i i i ∣ ∣ . . . ∣ ∣ 2 ||...||^2 ∣∣...∣ ∣ 2
我们需要计算所有点到其簇的平方距离,例如 C 5 ( 1.8 , 9.0 ) C5(1.8, 9.0) C 5 ( 1.8 , 9.0 ) ( 1.8 − 8.0 ) 2 + ( 9.0 − 8.5 ) 2 = ( − 6.2 ) 2 + ( 0.5 ) 2 = 38.44 + 0.25 = 38.69 (1.8-8.0)^2 + (9.0-8.5)^2 = (-6.2)^2 + (0.5)^2 = 38.44 + 0.25 = \mathbf{38.69} ( 1.8 − 8.0 ) 2 + ( 9.0 − 8.5 ) 2 = ( − 6.2 ) 2 + ( 0.5 ) 2 = 38.44 + 0.25 = 38.69
将这些距离的平方相加后除样本数 6 6 6 S S E 1 = 0 + 0.5 + 0 + 1.25 + 38.69 + 1.25 = 41.69 SSE_{1} = 0 + 0.5 + 0 + 1.25 + 38.69 + 1.25 = \mathbf{41.69} SS E 1 = 0 + 0.5 + 0 + 1.25 + 38.69 + 1.25 = 41.69 M S E 1 = 41.69 6 ≈ 6.948 MSE_{1} = \frac{41.69}{6} \approx \mathbf{6.948} MS E 1 = 6 41.69 ≈ 6.948
更新中心 (Update) :根据分配结果,重新计算中心点(即计算簇内所有点的平均值) 。
新簇 1 M 1 M_1 M 1 ( ( 1.5 + 2.0 ) / 2 , ( 2.0 + 2.5 ) / 2 ) = ( 1.75 , 2.25 ) ((1.5+2.0)/2, (2.0+2.5)/2) = (1.75, 2.25) (( 1.5 + 2.0 ) /2 , ( 2.0 + 2.5 ) /2 ) = ( 1.75 , 2.25 ) M 1 = ( 1.75 , 2.25 ) M_1 = (1.75, 2.25) M 1 = ( 1.75 , 2.25 )
新簇 2 M 2 M_2 M 2 ( 27.3 / 4 , 33.0 / 4 ) = ( 6.825 , 8.25 ) (27.3/4, 33.0/4) = (6.825, 8.25) ( 27.3/4 , 33.0/4 ) = ( 6.825 , 8.25 ) M 2 = ( 6.825 , 8.25 ) M_2 = (6.825, 8.25) M 2 = ( 6.825 , 8.25 )
计算更新后的误差 (Error After Update) :根据新的簇坐标,重新计算距离得到新的误差。
S S E 2 = 0.125 + 0.125 + 1.443 + 3.368 + 25.813 + 4.793 = 35.668 SSE_{2} = 0.125 + 0.125 + 1.443 + 3.368 + 25.813 + 4.793 = \mathbf{35.668} SS E 2 = 0.125 + 0.125 + 1.443 + 3.368 + 25.813 + 4.793 = 35.668
M S E 2 = 35.668 6 ≈ 5.945 MSE_{2} = \frac{35.668}{6} \approx \mathbf{5.945} MS E 2 = 6 35.668 ≈ 5.945
可以看到,误差减小了。
迭代 :使用新的中心点再次计算距离并重新分配。重复步骤 1-4,当分配不再改变时 ,算法收敛 (Converged)。
我们可以手动模拟一下第二次迭代如图:
可以发现分配没有改变,算法收敛。
Part 2 第二阶段:异常检测 (Anomaly Detection)
聚类的过程中,我们发现难免有些数据会离群。例如,C5 被分配给簇 2,但 C5 的特征值离簇 2 的中心点太远了。在考试中,会要求我们根据数据计算阈值,并判断异常点。
下面的步骤可以进行 基于统计的异常检测 :
计算簇内距离 (Intra-cluster Distances) :我们需要计算每个点到它最终归属的簇中心的距离。这个在我们前面计算 MSE 的时候已经计算过了。
可以发现,C1, C2 距离簇 1 中心都很近 (≈ 0.354 \approx 0.354 ≈ 0.354 1.2 ∼ 2.2 1.2 \sim 2.2 1.2 ∼ 2.2 ( 6.825 , 8.25 ) (6.825, 8.25) ( 6.825 , 8.25 )
统计学判定 (Statistical Thresholding) :不能光凭感觉说 5.081 很大,我们需要一个统计标准。根据经验公式,一般采用 M e a n + 1.5 × S t d D e v Mean + 1.5 \times StdDev M e an + 1.5 × St d De v M e a n Mean M e an S t d D e v StdDev St d De v
计算 均值 (Mean) : 所有 6 个距离 (d i d_i d i μ ≈ 1.836 \mu \approx 1.836 μ ≈ 1.836
计算 标准差 (Std Dev) : 根据计算得到的均值,带入标准差公式测算距离波动的大小。
σ = 1 N ∑ i = 1 N ( d i − μ ) 2 \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (d_i - \mu)^2} σ = N 1 i = 1 ∑ N ( d i − μ ) 2 带入数据,σ ≈ 1.605 \sigma \approx 1.605 σ ≈ 1.605
计算 阈值 (Threshold) : μ + 1.5 × σ ≈ 2.05 \mu + 1.5 \times \sigma \approx 2.05 μ + 1.5 × σ ≈ 2.05
T h r e s h o l d = μ + 1.5 × σ = 1.836 + 1.5 × 1.605 = 4.244 \begin{align*}
Threshold &= \mu + 1.5 \times \sigma \\
&= 1.836 + 1.5 \times 1.605 \\
&= 4.244
\end{align*} T h res h o l d = μ + 1.5 × σ = 1.836 + 1.5 × 1.605 = 4.244
判定异常点 (Detect Anomalies) :如果某个点到簇中心的距离超过了阈值,则判定为异常点。根据我们计算得到的数据,C5 的距离 (5.081) > 阈值 (4.244)。所以 C5 是异常点 (Outlier)。
我们可以将其进行业务上的分析:C5 可能是一个极低消费但极高满意度的客户,这在统计上是不符合常理的(可能是数据录入错误,或者是薅羊毛用户),因此被识别为异常。
总结:
K-means 流程 : “分配 -> 更新 -> 分配 -> 更新”,直到不动为止。异常检测逻辑 : 这里的异常不是指“离原点远”,而是指“离所属簇的中心远”。 Task 4: 隐变量模型 —— EM 算法# 在数据挖掘中,我们观察到的叫“观测变量”(比如:考试成绩、购买记录)。很多现实数据的生成机制里,存在一些你没观测到、但确实在影响结果的因素,例如:一门课的成绩分布可能来自两类学生群体(基础好/基础弱),但你并不知道具体的每个学生属于哪类;或一段时间序列的当前状态(健康/故障、冷/热)是隐藏的,但你只观测到传感器读数。
这些“看不见的因素”就是 隐变量 (Latent Variable) 。
具体而言,我们通过一个例子来了解:
想象这样一个场景:你是一个老师,你手里有一叠试卷,包含 A、B、C、D 四个等级。你想统计每种等级的 概率分布 (比如得 A 的概率是多少,得 B 的是多少…)。 通常情况下,这很简单:数一下 A 多少张,B 多少张,除以总数就行了。这种计算方法在概率与统计中称为 最大似然估计 (Maximum Likelihood Estimation, MLE) 。
如果,每个等级的数量都知道了,每一个概率分布都可以直接计算。但是,现在出了个问题,助教把试卷搞乱了。
他明确分出了 C 等级和 D 等级的卷子。但是,他把 A 等级和 B 等级的卷子混在了一个袋子里,统称为 “High grades” (h h h
你的任务是找出 B 等级的概率(我们称为 μ \mu μ
如果我想算出 μ \mu μ b b b
如果我想知道袋子里有几张 B (b b b μ \mu μ
这样因为缺少了关键的隐变量而陷入死循环的问题模型我们称为 隐变量模型 (Latent Variable Model) 。
EM 算法 (Expectation-Maximization Algorithm) 提供了解决隐变量模型的思路:既然解不开,那就先猜一个 !
先随便猜一个 μ \mu μ μ = 0 \mu=0 μ = 0
E-Step (填空):基于这个猜测的 μ \mu μ
M-Step (更新):把你估算的 B 的数量当成“真实数据”,重新计算最合理的 μ \mu μ
循环:用新的 μ \mu μ
对于上面这样的问题,我们建模如下:
观测数据 (Observed Data): 我们确实看到的,h h h c c c d d d
隐变量 (Latent Data) : 我们看不到的细节,a a a b b b 参数 (Parameters) : 控制概率分布的变量,这里是 μ \mu μ μ = 0 \mu = 0 μ = 0 在每次 μ \mu μ μ \mu μ h h h
b ( t ) = E [ B ∣ Observed Data , μ ( t ) ] b^{(t)} = E[B | \text{Observed Data}, \mu^{(t)}] b ( t ) = E [ B ∣ Observed Data , μ ( t ) ] 接下来,我们假设 E-step 算出来的 b b b μ \mu μ
μ ( t + 1 ) = argmax μ P ( Complete Data ∣ μ ) \mu^{(t+1)} = \text{argmax}_{\mu} \ P(\text{Complete Data} | \mu) μ ( t + 1 ) = argmax μ P ( Complete Data ∣ μ ) 现在我们带着这套逻辑回到下面的题目中。下面的部分在考试中将会被要求解答。
考试成绩分 A, B, C, D 四档。
观测数据 (Observed Data): h = 20 h = 20 h = 20
c = 10 c = 10 c = 10 d = 10 d = 10 d = 10 总人数 N = 40 N = 40 N = 40
成绩分布符合某种概率(下面给出的是散点的情况,连续的情况可能是某些常见的概率密度函数):
P ( A ) = 0.5 P(A) = 0.5 P ( A ) = 0.5 P ( B ) = μ P(B) = \mu P ( B ) = μ P ( C ) = 2 μ P(C) = 2\mu P ( C ) = 2 μ P ( D ) = 0.5 − 3 μ P(D) = 0.5 - 3\mu P ( D ) = 0.5 − 3 μ 注:所有概率加起来 0.5 + μ + 2 μ + 0.5 − 3 μ = 1.0 0.5 + \mu + 2\mu + 0.5 - 3\mu = 1.0 0.5 + μ + 2 μ + 0.5 − 3 μ = 1.0
Step 1 E-Step: 期望步 (Expectation) —— “填补缺失数据”
假设当前的 μ \mu μ h = 20 h=20 h = 20
A 和 B 的总权重是 0.5 + μ 0.5 + \mu 0.5 + μ
因此,在 一个 “High grade”样本中,它是 B 的概率(条件概率)是:
P ( B ∣ H i g h ) = P ( B ) P ( A ) + P ( B ) = μ 0.5 + μ P(B | High) = \frac{P(B)}{P(A) + P(B)} = \frac{\mu}{0.5 + \mu} P ( B ∣ H i g h ) = P ( A ) + P ( B ) P ( B ) = 0.5 + μ μ 对于所有的 “High grade” 样本,其中 B 的数量为:
b ( t ) = h × μ ( t ) 0.5 + μ ( t ) = 20 × μ ( t ) 0.5 + μ ( t ) \begin{equation}
b^{(t)} = h \times \frac{\mu^{(t)}}{0.5 + \mu^{(t)}} = 20 \times \frac{\mu^{(t)}}{0.5 + \mu^{(t)}}
\end{equation} b ( t ) = h × 0.5 + μ ( t ) μ ( t ) = 20 × 0.5 + μ ( t ) μ ( t ) b ( t ) b^{(t)} b ( t ) t t t μ \mu μ 从 0 开始 。
Step 2 M-Step: 最大化步 (Maximization) —— “更新规则”
假设刚才估算出来的 b ( t ) b^{(t)} b ( t ) μ \mu μ
这需要用到最大似然估计 (MLE)。首先是构造最大化似然函数 L ( μ ) L(\mu) L ( μ ) L L L 所有观测次数的乘积 :
L ( μ ) = K ⋅ P ( A ) a ⋅ P ( B ) b ⋅ P ( C ) c ⋅ P ( D ) d = K ⋅ ( 1 / 2 ) a ⋅ μ b ⋅ ( 2 μ ) c ⋅ ( 0.5 − 3 μ ) d L(\mu) = K \cdot P(A)^a \cdot P(B)^b \cdot P(C)^c \cdot P(D)^d = K \cdot (1/2)^a \cdot \mu^b \cdot (2\mu)^c \cdot (0.5 - 3\mu)^d L ( μ ) = K ⋅ P ( A ) a ⋅ P ( B ) b ⋅ P ( C ) c ⋅ P ( D ) d = K ⋅ ( 1/2 ) a ⋅ μ b ⋅ ( 2 μ ) c ⋅ ( 0.5 − 3 μ ) d K K K n n n n = a + b + c + d n = a+b+c+d n = a + b + c + d K = n ! a ! b ! c ! d ! K = \frac{n!}{a!b!c!d!} K = a ! b ! c ! d ! n ! 不包含 μ \mu μ
以上是离散数据分布的情况,如果是连续的概率分布,假设你有一组观测值 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x 1 , x 2 , … , x n θ \theta θ f ( x ∣ θ ) f(x|\theta) f ( x ∣ θ )
L ( θ ) = f ( x 1 ∣ θ ) ⋅ f ( x 2 ∣ θ ) … f ( x n ∣ θ ) = ∏ i = 1 n f ( x i ∣ θ ) L(\theta) = f(x_1|\theta) \cdot f(x_2|\theta) \dots f(x_n|\theta) = \prod_{i=1}^{n} f(x_i|\theta) L ( θ ) = f ( x 1 ∣ θ ) ⋅ f ( x 2 ∣ θ ) … f ( x n ∣ θ ) = i = 1 ∏ n f ( x i ∣ θ ) 要求最有可能的 μ \mu μ L ( μ ) L(\mu) L ( μ ) 求偏导 。可以发现因为其表达式通常携带次方不便于计算,为了好计算,我们取对数 (Log-Likelihood):
ln ( L ( μ ) ) = ln K ⋅ a ln ( 1 / 2 ) ⋅ b ln ( μ ) ⋅ c ln ( 2 μ ) ⋅ d ln ( 0.5 − 3 μ ) \ln(L(\mu)) = \ln K \cdot a\ln(1/2) \cdot b\ln(\mu) \cdot c\ln(2\mu) \cdot d\ln(0.5 - 3\mu) ln ( L ( μ )) = ln K ⋅ a ln ( 1/2 ) ⋅ b ln ( μ ) ⋅ c ln ( 2 μ ) ⋅ d ln ( 0.5 − 3 μ ) 对 μ \mu μ
∂ ln L ∂ μ = b μ + 2 c 2 μ − 3 d 0.5 − 3 μ = 0 ⟹ b + c μ = 3 d 0.5 − 3 μ ⟹ ( b + c ) ( 0.5 − 3 μ ) = 3 d μ ⟹ 0.5 ( b + c ) = 3 μ ( d + b + c ) ⟹ μ = b + c 6 ( b + c + d ) \begin{align*}
&\frac{\partial \ln L}{\partial \mu} = \frac{b}{\mu} + \frac{2c}{2\mu} - \frac{3d}{0.5 - 3\mu} = 0 \\
&\implies \frac{b+c}{\mu} = \frac{3d}{0.5 - 3\mu} \\
&\implies (b+c)(0.5 - 3\mu) = 3d\mu \\
&\implies 0.5(b+c) = 3\mu(d + b + c) \\
&\implies \mu = \frac{b+c}{6(b+c+d)}
\end{align*} ∂ μ ∂ ln L = μ b + 2 μ 2 c − 0.5 − 3 μ 3 d = 0 ⟹ μ b + c = 0.5 − 3 μ 3 d ⟹ ( b + c ) ( 0.5 − 3 μ ) = 3 d μ ⟹ 0.5 ( b + c ) = 3 μ ( d + b + c ) ⟹ μ = 6 ( b + c + d ) b + c 于是我们就可以得到了 M-Step 的递推公式:
μ ( t + 1 ) = b ( t ) + c 6 ( b ( t ) + c + d ) \begin{equation}
\mu^{(t+1)} = \frac{b^{(t)} + c}{6(b^{(t)} + c + d)}
\end{equation} μ ( t + 1 ) = 6 ( b ( t ) + c + d ) b ( t ) + c t t t
Step 3 循环迭代
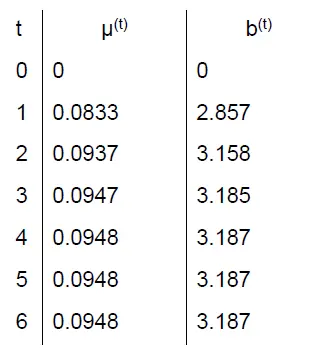
初始条件下,h = 20 , c = 10 , d = 10 h=20, c=10, d=10 h = 20 , c = 10 , d = 10 μ ( 0 ) = 0 \mu^{(0)} = 0 μ ( 0 ) = 0
第 1 轮迭代 (Iteration 1)
E-Step (算 B 的数量 ):
b ( 0 ) = 20 × 0 0.5 + 0 = 0 b^{(0)} = 20 \times \frac{0}{0.5 + 0} = 0 b ( 0 ) = 20 × 0.5 + 0 0 = 0 这意味着,既然 B 的概率是 0,那这 20 个高分肯定全是 A。
M-Step (更新 μ \mu μ ): 现在的“完整数据”是:b = 0 , c = 10 , d = 10 b=0, c=10, d=10 b = 0 , c = 10 , d = 10
μ ( 1 ) = 0 + 10 6 ( 0 + 10 + 10 ) = 10 120 = 0.0833 \mu^{(1)} = \frac{0 + 10}{6(0 + 10 + 10)} = \frac{10}{120} = 0.0833 μ ( 1 ) = 6 ( 0 + 10 + 10 ) 0 + 10 = 120 10 = 0.0833
第 2 轮迭代 (Iteration 2)
E-Step (算 B 的数量): 现在用新的 μ = 0.0833 \mu = 0.0833 μ = 0.0833 0.5 0.5 0.5 0.0833 0.0833 0.0833 0.0833 0.5 + 0.0833 = 0.0833 0.5833 ≈ 0.1428 \frac{0.0833}{0.5 + 0.0833} = \frac{0.0833}{0.5833} \approx 0.1428 0.5 + 0.0833 0.0833 = 0.5833 0.0833 ≈ 0.1428
b ( 1 ) = 20 × 0.1428 ≈ 2.857 b^{(1)} = 20 \times 0.1428 \approx 2.857 b ( 1 ) = 20 × 0.1428 ≈ 2.857 概率更新了,我们推测这 20 个人里大概有 2.857 个人其实是 B。
M-Step (更新 μ \mu μ b = 2.857 , c = 10 , d = 10 b=2.857, c=10, d=10 b = 2.857 , c = 10 , d = 10
μ ( 2 ) = 2.857 + 10 6 ( 2.857 + 10 + 10 ) = 12.857 6 ( 22.857 ) = 12.857 137.142 ≈ 0.0937 \mu^{(2)} = \frac{2.857 + 10}{6(2.857 + 10 + 10)} = \frac{12.857}{6(22.857)} = \frac{12.857}{137.142} \approx 0.0937 μ ( 2 ) = 6 ( 2.857 + 10 + 10 ) 2.857 + 10 = 6 ( 22.857 ) 12.857 = 137.142 12.857 ≈ 0.0937
第 3 轮迭代 (Iteration 3)
E-Step: μ = 0.0937 \mu = 0.0937 μ = 0.0937
b ( 2 ) = 20 × 0.0937 0.5 + 0.0937 = 20 × 0.0937 0.5937 ≈ 3.158 b^{(2)} = 20 \times \frac{0.0937}{0.5 + 0.0937} = 20 \times \frac{0.0937}{0.5937} \approx 3.158 b ( 2 ) = 20 × 0.5 + 0.0937 0.0937 = 20 × 0.5937 0.0937 ≈ 3.158 B 的数量在进一步增加,逐渐趋近真实数量。
M-Step:
μ ( 3 ) = 3.158 + 10 6 ( 3.158 + 10 + 10 ) ≈ 0.0947 \mu^{(3)} = \frac{3.158 + 10}{6(3.158 + 10 + 10)} \approx 0.0947 μ ( 3 ) = 6 ( 3.158 + 10 + 10 ) 3.158 + 10 ≈ 0.0947
第 4 轮迭代 (Iteration 4)
E-Step: μ = 0.0947 \mu = 0.0947 μ = 0.0947
b ( 3 ) = 20 × 0.0947 0.5 + 0.0947 = 20 × 0.0947 0.5947 ≈ 3.185 b^{(3)} = 20 \times \frac{0.0947}{0.5 + 0.0947} = 20 \times \frac{0.0947}{0.5947} \approx 3.185 b ( 3 ) = 20 × 0.5 + 0.0947 0.0947 = 20 × 0.5947 0.0947 ≈ 3.185
M-Step:
μ ( 4 ) = 3.185 + 10 6 ( 3.185 + 10 + 10 ) ≈ 0.0948 \mu^{(4)} = \frac{3.185 + 10}{6(3.185 + 10 + 10)} \approx 0.0948 μ ( 4 ) = 6 ( 3.185 + 10 + 10 ) 3.185 + 10 ≈ 0.0948
第 5 轮迭代 (Iteration 5)
E-Step: μ = 0.0948 \mu = 0.0948 μ = 0.0948
b ( 3 ) = 20 × 0.0948 0.5 + 0.0948 = 20 × 0.0948 0.5948 ≈ 3.187 b^{(3)} = 20 \times \frac{0.0948}{0.5 + 0.0948} = 20 \times \frac{0.0948}{0.5948} \approx 3.187 b ( 3 ) = 20 × 0.5 + 0.0948 0.0948 = 20 × 0.5948 0.0948 ≈ 3.187
M-Step:
μ ( 4 ) = 3.187 + 10 6 ( 3.187 + 10 + 10 ) ≈ 0.0948 \mu^{(4)} = \frac{3.187 + 10}{6(3.187 + 10 + 10)} \approx 0.0948 μ ( 4 ) = 6 ( 3.187 + 10 + 10 ) 3.187 + 10 ≈ 0.0948
你会发现 μ \mu μ
总结与练习# 在这里对以上四个经典任务的解题过程与核心思路进行总结。
Task 1 Task 1: 文档相似度分析 (TF-IDF & Cosine Similarity) :将非结构化的“文本”转化为计算机可计算的“数值向量”。
解题过程:
预处理 (Pre-processing) : 根据停用词表清洗数据,只保留有意义的关键词。词频统计 (Term Frequency) : 统计关键词在当前文档中的出现频率。T F = 词次数 文档总词数 TF = \frac{\text{词次数}}{\text{文档总词数}} TF = 文档总词数 词次数 加权计算 (IDF) : 惩罚常见词,奖励稀有词。I D F = log ( 文档总数 包含该词的文档数 ) IDF = \log(\frac{\text{文档总数}}{\text{包含该词的文档数}}) I D F = log ( 包含该词的文档数 文档总数 ) 向量化 (Vectorization) :计算生成 TF-IDF 矩阵。每一行是一个文档的特征向量。相似度计算 (Cosine Similarity) : 使用余弦相似度公式 A ⋅ B ∣ ∣ A ∣ ∣ × ∣ ∣ B ∣ ∣ \frac{A \cdot B}{||A|| \times ||B||} ∣∣ A ∣∣ × ∣∣ B ∣∣ A ⋅ B 不要只看词出现的次数,要看词的信息量(IDF)。相似度本质上是看两个向量在多维空间中方向是否一致,而不是看它们的长短。
Task 2 Task 2: 最小哈希 (MinHash) :大规模二进制数据的快速降维与近似。
这是一种“以小见大”的概率算法。通过多次随机置换抓取特征,我们将庞大的高维稀疏向量压缩成了极短的签名向量,虽然牺牲了一点精度,但换取了极高的计算效率。
解题过程:
数据转换 :忽略词频,将文档转化为 0/1 的二进制向量 (One-hot)。置换 (Permutation) : 随机打乱列(关键词)的顺序。你需要根据置换向量 P P P 签名生成 (Signature) : 在新的顺序下,找到第一个 “1” 出现的位置索引。这个索引就是签名值。相似度估算 : 比较两个文档的签名向量。签名相同的比例 ≈ \approx ≈ Jaccard 相似度 (交集/并集)。 Task 3 Task 3: 聚类与异常检测 (Clustering & Anomaly Detection) :发现数据的自然分组,并基于分组识别离群点。
解题过程:
分配 (Assignment) :计算每个样本点到现有中心点的欧几里得距离,将其归入最近的簇。更新 (Update) : 计算簇内所有点的均值 (Mean),以此作为新的中心点。这一步旨在最小化均方误差 (MSE)。迭代 (Iterate) : 重复上述两步,直到中心点不再移动(收敛)。异常检测 :计算每个点到其所属簇中心的距离。计算距离的均值和标准差。设定阈值 (如 Mean + 1.5 × \times × K-means 是通过不断调整中心点来让簇内差异最小化。而异常是相对的——不是看你离原点有多远,而是看你离你的“组织”(簇中心)有多远。
Task 4 Task 4: 潜变量模型 (EM Algorithm) :在数据缺失的情况下,通过“猜测-验证”循环来估计参数。
当变量互相依赖无法直接求解时,先猜一个,然后用数据修正它。这是一个从“不确定”走向“确定”的收敛过程。
解题过程:
初始化 :给未知参数 μ \mu μ E-Step (期望) : 假设 μ \mu μ P ( B ∣ High ) = μ α + μ P(B|\text{High}) = \frac{\mu}{\alpha+\mu} P ( B ∣ High ) = α + μ μ h h h b b b M-Step (最大化) : 假设估算的 b b b μ \mu μ μ \mu μ 迭代 : 反复执行 E-M 步骤,直到 μ \mu μ 下面是基于例题的对于上述四种任务的一些练习,用于巩固这些知识。
(Task 1) 有 3 篇文档,我们已经去除了停用词,并确定了 5 个关键词的词汇表:V = { AI, data, model, train, code } V = \{\text{AI, data, model, train, code}\} V = { AI, data, model, train, code }
D1: “AI model train AI” (4 words)
D2: “data model code” (3 words)
D3: “AI train code” (3 words)
任务:
计算 IDF : 计算词汇表中所有 5 个词的 IDF 值(使用 log 10 \log_{10} log 10 ln \ln ln log 10 \log_{10} log 10 构建 TF-IDF 矩阵 : 计算 D1 和 D3 的 TF-IDF 特征向量 (使用词袋模型,Bag-of-Words model)。计算相似度 : 计算 D1 和 D3 之间的余弦相似度 (Cosine Similarity)。
(提示:N = 3 N=3 N = 3 I D F ( t ) = log 10 ( N D F ( t ) ) IDF(t) = \log_{10}(\frac{N}{DF(t)}) I D F ( t ) = log 10 ( D F ( t ) N ) Sim = A ⋅ B ∣ ∣ A ∣ ∣ × ∣ ∣ B ∣ ∣ \text{Sim} = \frac{A \cdot B}{||A|| \times ||B||} Sim = ∣∣ A ∣∣ × ∣∣ B ∣∣ A ⋅ B
IDF 计算 (N = 3 N=3 N = 3
AI: 出现在 D1, D3 → D F = 2 → I D F = log ( 3 / 2 ) = 0.176 \rightarrow DF=2 \rightarrow IDF = \log(3/2) = 0.176 → D F = 2 → I D F = log ( 3/2 ) = 0.176
data: 出现在 D2 → D F = 1 → I D F = log ( 3 / 1 ) = 0.477 \rightarrow DF=1 \rightarrow IDF = \log(3/1) = 0.477 → D F = 1 → I D F = log ( 3/1 ) = 0.477
model: 出现在 D1, D2 → D F = 2 → I D F = 0.176 \rightarrow DF=2 \rightarrow IDF = 0.176 → D F = 2 → I D F = 0.176
train: 出现在 D1, D3 → D F = 2 → I D F = 0.176 \rightarrow DF=2 \rightarrow IDF = 0.176 → D F = 2 → I D F = 0.176
code: 出现在 D2, D3 → D F = 2 → I D F = 0.176 \rightarrow DF=2 \rightarrow IDF = 0.176 → D F = 2 → I D F = 0.176
TF-IDF 向量构建 :
D1 Vector (AI:2, model:1, train:1, others:0 / Total: 4),所以 T F ( AI , D 1 ) = 2 / 4 = 0.5 TF(\text{AI}, D1) = 2 / 4 = 0.5 TF ( AI , D 1 ) = 2/4 = 0.5 T F ( model , D 1 ) = 1 / 4 = 0.25 TF(\text{model}, D1) = 1 / 4 = 0.25 TF ( model , D 1 ) = 1/4 = 0.25 T F ( train , D 1 ) = 1 / 4 = 0.25 TF(\text{train}, D1) = 1 / 4 = 0.25 TF ( train , D 1 ) = 1/4 = 0.25
于是对于每一个词,带入 TF-IDF 公式中可以得到:
AI: 0.5 × 0.176 = 0.088 0.5 \times 0.176 = 0.088 0.5 × 0.176 = 0.088
data: 0 0 0
model: 0.25 × 0.176 = 0.044 0.25 \times 0.176 = 0.044 0.25 × 0.176 = 0.044
train: 0.25 × 0.176 = 0.044 0.25 \times 0.176 = 0.044 0.25 × 0.176 = 0.044
code: 0 0 0
D1 的向量矩阵为:D 1 ⃗ = [ 0.088 , 0 , 0.044 , 0.044 , 0 ] \vec{D1} = [0.088, 0, 0.044, 0.044, 0] D 1 = [ 0.088 , 0 , 0.044 , 0.044 , 0 ]
D3 Vector (AI:1, train:1, code:1 / Total: 3),所以 T F ( AI , D 3 ) = T F ( train , D 3 ) = T F ( code , D 3 ) = 1 / 3 = 0.333 TF(\text{AI}, D3) = TF(\text{train}, D3) = TF(\text{code}, D3) = 1/3 = 0.333 TF ( AI , D 3 ) = TF ( train , D 3 ) = TF ( code , D 3 ) = 1/3 = 0.333
对于每一个词,带入 TF-IDF 公式中可以得到:
AI: 0.333 × 0.176 ≈ 0.059 0.333 \times 0.176 \approx 0.059 0.333 × 0.176 ≈ 0.059
data: 0 0 0
model: 0 0 0
train: 0.333 × 0.176 ≈ 0.059 0.333 \times 0.176 \approx 0.059 0.333 × 0.176 ≈ 0.059
code: 0.333 × 0.176 ≈ 0.059 0.333 \times 0.176 \approx 0.059 0.333 × 0.176 ≈ 0.059
D3 的向量矩阵为:D 3 ⃗ = [ 0.059 , 0 , 0 , 0.059 , 0.059 ] \vec{D3} = [0.059, 0, 0, 0.059, 0.059] D 3 = [ 0.059 , 0 , 0 , 0.059 , 0.059 ]
余弦相似度计算 :根据公式,我们需要计算两个向量相乘及其模长。
点积 (Dot Product): D 1 ⃗ × D 3 ⃗ = 0.088 × 0.059 + 0.044 × 0.059 = 0.007788 \vec{D1} \times \vec{D3} = 0.088 \times 0.059 + 0.044 \times 0.059 = 0.007788 D 1 × D 3 = 0.088 × 0.059 + 0.044 × 0.059 = 0.007788
模长 (Magnitude):
∣ ∣ D 1 ∣ ∣ = 0.088 2 + 0.044 2 + 0.044 2 = 0.007744 + 0.001936 + 0.001936 = 0.011616 ≈ 0.1078 ||D1|| = \sqrt{0.088^2 + 0.044^2 + 0.044^2} = \sqrt{0.007744 + 0.001936 + 0.001936} = \sqrt{0.011616} \approx 0.1078 ∣∣ D 1∣∣ = 0.08 8 2 + 0.04 4 2 + 0.04 4 2 = 0.007744 + 0.001936 + 0.001936 = 0.011616 ≈ 0.1078 ∣ ∣ D 3 ∣ ∣ = 0.059 2 + 0.059 2 + 0.059 2 = 3 × 0.003481 = 0.010443 ≈ 0.1022 ||D3|| = \sqrt{0.059^2 + 0.059^2 + 0.059^2} = \sqrt{3 \times 0.003481} = \sqrt{0.010443} \approx 0.1022 ∣∣ D 3∣∣ = 0.05 9 2 + 0.05 9 2 + 0.05 9 2 = 3 × 0.003481 = 0.010443 ≈ 0.1022
带入公式计算相似度可以得到:
S i m = 0.007788 0.1078 × 0.1022 = 0.007788 0.011017 ≈ 0.707 Sim = \frac{0.007788}{0.1078 \times 0.1022} = \frac{0.007788}{0.011017} \approx 0.707 S im = 0.1078 × 0.1022 0.007788 = 0.011017 0.007788 ≈ 0.707
(Task 2) 有两个文档的二进制向量,长度为 8 (对应 8 个特征)。D 1 ⃗ = [ 0 , 1 , 1 , 0 , 0 , 1 , 0 , 1 ] \vec{D1} = [0, 1, 1, 0, 0, 1, 0, 1] D 1 = [ 0 , 1 , 1 , 0 , 0 , 1 , 0 , 1 ] D 2 ⃗ = [ 1 , 0 , 1 , 0 , 1 , 1 , 0 , 0 ] \vec{D2} = [1, 0, 1, 0, 1, 1, 0, 0] D 2 = [ 1 , 0 , 1 , 0 , 1 , 1 , 0 , 0 ]
任务:利用以下 3 个随机置换 (Permutations) 计算签名矩阵,并估算相似度。
P 1 ⃗ = [ 2 , 4 , 6 , 8 , 1 , 3 , 5 , 7 ] \vec{P1} = [2, 4, 6, 8, 1, 3, 5, 7] P 1 = [ 2 , 4 , 6 , 8 , 1 , 3 , 5 , 7 ]
P 2 ⃗ = [ 5 , 1 , 8 , 2 , 6 , 3 , 7 , 4 ] \vec{P2} = [5, 1, 8, 2, 6, 3, 7, 4] P 2 = [ 5 , 1 , 8 , 2 , 6 , 3 , 7 , 4 ]
P 3 ⃗ = [ 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 ] \vec{P3} = [8, 7, 6, 5, 4, 3, 2, 1] P 3 = [ 8 , 7 , 6 , 5 , 4 , 3 , 2 , 1 ]
构造 D1 和 D2 的 签名向量 (每个向量包含 3 个签名值)。
计算 MinHash 估算的相似度 。
计算 真实的 Jaccard 相似度 ,并 比较误差 。
签名向量其实是经过随机置换后找到的第一个 “1” 的位置的向量,我们对两个文档应用三个随机置换向量:
D 1 ⃗ \vec{D1} D 1
应用 P 1 P1 P 1 1 1 1
应用 P 2 P2 P 2 3 3 3
应用 P 3 P3 P 3 1 1 1 Sign D 1 = [ 1 , 3 , 1 ] \text{Sign}_{D1} = [1,3,1] Sign D 1 = [ 1 , 3 , 1 ]
D 2 ⃗ \vec{D2} D 2
应用 P 1 P1 P 1 3 3 3
应用 P 2 P2 P 2 1 1 1
应用 P 3 P3 P 3 3 3 3 Sign D 1 = [ 3 , 1 , 3 ] \text{Sign}_{D1} = [3,1,3] Sign D 1 = [ 3 , 1 , 3 ]
接下来需要计算其估算的相似度,使用两个文档的签名向量。注意:这里的相似度是 每一位是否相同 的比较,而不是余弦相似度。比较 [ 1 , 3 , 1 ] [1, 3, 1] [ 1 , 3 , 1 ] [ 3 , 1 , 3 ] [3, 1, 3] [ 3 , 1 , 3 ]
Pos 1: 1 ≠ 3 1 \neq 3 1 = 3
Pos 2: 3 ≠ 1 3 \neq 1 3 = 1
Pos 3: 1 ≠ 3 1 \neq 3 1 = 3
S i m MinHash = 0 / 3 = 0 Sim_{\text{MinHash}} = 0 / 3 = 0 S i m MinHash = 0/3 = 0 最后,我们需要计算真实的 Jaccard 相似度和误差,Jaccard 相似度为 两文档中 1 的位置的交集 两文档中 1 的位置的并集 \frac{\text{两文档中 1 的位置的交集}}{\text{两文档中 1 的位置的并集}} 两文档中 1 的位置的并集 两文档中 1 的位置的交集
D 1 ⃗ = [ 0 , 1 , 1 , 0 , 0 , 1 , 0 , 1 ] \vec{D1} = [0, 1, 1, 0, 0, 1, 0, 1] D 1 = [ 0 , 1 , 1 , 0 , 0 , 1 , 0 , 1 ] D 2 ⃗ = [ 1 , 0 , 1 , 0 , 1 , 1 , 0 , 0 ] \vec{D2} = [1, 0, 1, 0, 1, 1, 0, 0] D 2 = [ 1 , 0 , 1 , 0 , 1 , 1 , 0 , 0 ]
所以:
交集:{ 3 , 6 } \{3,6\} { 3 , 6 } 2 2 2
并集:{ 1 , 2 , 3 , 5 , 6 , 8 } \{1,2,3,5,6,8\} { 1 , 2 , 3 , 5 , 6 , 8 } 6 6 6
S i m Jaccard = 2 / 6 = 0.333 Sim_{\text{Jaccard}} = 2 / 6 = 0.333 S i m Jaccard = 2/6 = 0.333 误差就是它们之间的差的绝对值:E r r = ∣ S i m Jaccard − S i m MinHash ∣ = 0.333 Err = |Sim_{\text{Jaccard}} - Sim_{\text{MinHash}}| = 0.333 E rr = ∣ S i m Jaccard − S i m MinHash ∣ = 0.333
这可以说明,当哈希函数数量较少时,MinHash 的波动可能很大。
(Task 3) 一家电商平台收集了 5 位用户的行为数据,包含两个特征(均为 0-10 分):
X 1 X_1 X 1 X 2 X_2 X 2
用户 X1 (价格) X2 (频率) A 2.0 2.0 B 2.0 4.0 C 10.0 8.0 D 10.0 10.0 E 10.0 2.0
任务:
我们使用 K-means 算法 (K = 2 K=2 K = 2
Cluster 1 中心: C 1 = A ( 2.0 , 2.0 ) C_1 = A (2.0, 2.0) C 1 = A ( 2.0 , 2.0 )
Cluster 2 中心: C 2 = C ( 10.0 , 8.0 ) C_2 = C (10.0, 8.0) C 2 = C ( 10.0 , 8.0 )
请完成以下计算步骤:
第一次迭代 (分配) : 计算各点到初始中心点的欧几里得距离,并将每个用户分配给最近的簇。第一次迭代 (更新) : 根据分配结果,计算新的簇中心坐标。异常检测 : 计算每个点到其 所属新簇中心 的距离。计算这些距离的 均值 (Mean) 和 标准差 (Std Dev) 。并使用阈值公式 T h r e s h o l d = M e a n + 1.5 × S t d D e v Threshold = Mean + 1.5 \times StdDev T h res h o l d = M e an + 1.5 × St d De v
第一次迭代:距离计算与分配
我们需要计算每个点 ( x , y ) (x, y) ( x , y ) C 1 ( 2 , 2 ) C_1(2, 2) C 1 ( 2 , 2 ) C 2 ( 10 , 8 ) C_2(10, 8) C 2 ( 10 , 8 ) d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2
用户 A (2, 2):
到 C 1 C_1 C 1
到 C 2 C_2 C 2 ( 2 − 10 ) 2 + ( 2 − 8 ) 2 = 64 + 36 = 10 \sqrt{(2-10)^2 + (2-8)^2} = \sqrt{64+36} = 10 ( 2 − 10 ) 2 + ( 2 − 8 ) 2 = 64 + 36 = 10
分配: Cluster 1
用户 B (2, 4):
到 C 1 C_1 C 1 ( 2 − 2 ) 2 + ( 4 − 2 ) 2 = 2 \sqrt{(2-2)^2 + (4-2)^2} = 2 ( 2 − 2 ) 2 + ( 4 − 2 ) 2 = 2
到 C 2 C_2 C 2 ( 2 − 10 ) 2 + ( 4 − 8 ) 2 = 64 + 16 ≈ 8.94 \sqrt{(2-10)^2 + (4-8)^2} = \sqrt{64+16} \approx 8.94 ( 2 − 10 ) 2 + ( 4 − 8 ) 2 = 64 + 16 ≈ 8.94
分配: Cluster 1
用户 C (10, 8):
到 C 1 C_1 C 1 ( 10 − 2 ) 2 + ( 8 − 2 ) 2 = 10 \sqrt{(10-2)^2 + (8-2)^2} = 10 ( 10 − 2 ) 2 + ( 8 − 2 ) 2 = 10
到 C 2 C_2 C 2
分配: Cluster 2
用户 D (10, 10):
到 C 1 C_1 C 1 8 2 + 8 2 ≈ 11.3 \sqrt{8^2 + 8^2} \approx 11.3 8 2 + 8 2 ≈ 11.3
到 C 2 C_2 C 2 ( 10 − 10 ) 2 + ( 10 − 8 ) 2 = 2 \sqrt{(10-10)^2 + (10-8)^2} = 2 ( 10 − 10 ) 2 + ( 10 − 8 ) 2 = 2
分配: Cluster 2
用户 E (10, 2):
到 C 1 C_1 C 1 ( 10 − 2 ) 2 + ( 2 − 2 ) 2 = 8 \sqrt{(10-2)^2 + (2-2)^2} = 8 ( 10 − 2 ) 2 + ( 2 − 2 ) 2 = 8
到 C 2 C_2 C 2 ( 10 − 10 ) 2 + ( 2 − 8 ) 2 = 6 \sqrt{(10-10)^2 + (2-8)^2} = 6 ( 10 − 10 ) 2 + ( 2 − 8 ) 2 = 6
分配: Cluster 2
初始的分配结果:
Cluster 1: {A, B}
Cluster 2: {C, D, E}
更新中心点 (Recalculate Centroids) :新中心点坐标为簇内所有点的坐标平均值。
New Cluster 1 Centroid:
X 1 = ( 2.0 + 2.0 ) / 2 = 2.0 X_1 = (2.0 + 2.0) / 2 = 2.0 X 1 = ( 2.0 + 2.0 ) /2 = 2.0 X 2 = ( 2.0 + 4.0 ) / 2 = 3.0 X_2 = (2.0 + 4.0) / 2 = 3.0 X 2 = ( 2.0 + 4.0 ) /2 = 3.0 新中心 M 1 : ( 2.0 , 3.0 ) M_1: (2.0, 3.0) M 1 : ( 2.0 , 3.0 )
New Cluster 2 Centroid:
X 1 = ( 10.0 + 10.0 + 10.0 ) / 3 = 10.0 X_1 = (10.0 + 10.0 + 10.0) / 3 = 10.0 X 1 = ( 10.0 + 10.0 + 10.0 ) /3 = 10.0 X 2 = ( 8.0 + 10.0 + 2.0 ) / 3 = 20 / 3 ≈ 6.67 X_2 = (8.0 + 10.0 + 2.0) / 3 = 20 / 3 \approx 6.67 X 2 = ( 8.0 + 10.0 + 2.0 ) /3 = 20/3 ≈ 6.67 新中心 M 2 : ( 10.0 , 6.67 ) M_2: (10.0, 6.67) M 2 : ( 10.0 , 6.67 )
在接下来的步骤中,将重复上述的分配和更新的过程,直到 分配没有改变 为止。
计算簇内距离 (Intra-cluster Distances) :计算每个点到它新中心的距离。
Cluster 1 (中心: 2.0, 3.0):
A (2, 2): ( 2 − 2 ) 2 + ( 2 − 3 ) 2 = 1.0 \sqrt{(2-2)^2 + (2-3)^2} = 1.0 ( 2 − 2 ) 2 + ( 2 − 3 ) 2 = 1.0
B (2, 4): ( 2 − 2 ) 2 + ( 4 − 3 ) 2 = 1.0 \sqrt{(2-2)^2 + (4-3)^2} = 1.0 ( 2 − 2 ) 2 + ( 4 − 3 ) 2 = 1.0
Cluster 2 (中心: 10.0, 6.67):
C (10, 8): ( 10 − 10 ) 2 + ( 8 − 6.67 ) 2 = 1.33 2 ≈ 1.33 \sqrt{(10-10)^2 + (8-6.67)^2} = \sqrt{1.33^2} \approx 1.33 ( 10 − 10 ) 2 + ( 8 − 6.67 ) 2 = 1.3 3 2 ≈ 1.33
D (10, 10): ( 10 − 10 ) 2 + ( 10 − 6.67 ) 2 = 3.33 2 ≈ 3.33 \sqrt{(10-10)^2 + (10-6.67)^2} = \sqrt{3.33^2} \approx 3.33 ( 10 − 10 ) 2 + ( 10 − 6.67 ) 2 = 3.3 3 2 ≈ 3.33
E (10, 2): ( 10 − 10 ) 2 + ( 2 − 6.67 ) 2 = ( − 4.67 ) 2 ≈ 4.67 \sqrt{(10-10)^2 + (2-6.67)^2} = \sqrt{(-4.67)^2} \approx 4.67 ( 10 − 10 ) 2 + ( 2 − 6.67 ) 2 = ( − 4.67 ) 2 ≈ 4.67
距离集合: [ 1.0 , 1.0 , 1.33 , 3.33 , 4.67 ] [1.0, 1.0, 1.33, 3.33, 4.67] [ 1.0 , 1.0 , 1.33 , 3.33 , 4.67 ]
均值 (Mean) :
M e a n = 1.0 + 1.0 + 1.33 + 3.33 + 4.67 5 = 11.33 5 ≈ 2.27 Mean = \frac{1.0+1.0+1.33+3.33+4.67}{5} = \frac{11.33}{5} \approx 2.27 M e an = 5 1.0 + 1.0 + 1.33 + 3.33 + 4.67 = 5 11.33 ≈ 2.27 标准差 (Std Dev) : (先算方差 Variance = 每个距离与均值的差的平方和 / N )
( 1.0 − 2.27 ) 2 = 1.61 (1.0 - 2.27)^2 = 1.61 ( 1.0 − 2.27 ) 2 = 1.61 ( 1.0 − 2.27 ) 2 = 1.61 (1.0 - 2.27)^2 = 1.61 ( 1.0 − 2.27 ) 2 = 1.61 ( 1.33 − 2.27 ) 2 = 0.88 (1.33 - 2.27)^2 = 0.88 ( 1.33 − 2.27 ) 2 = 0.88 ( 3.33 − 2.27 ) 2 = 1.12 (3.33 - 2.27)^2 = 1.12 ( 3.33 − 2.27 ) 2 = 1.12 ( 4.67 − 2.27 ) 2 = 5.76 (4.67 - 2.27)^2 = 5.76 ( 4.67 − 2.27 ) 2 = 5.76 Sum of Squares ≈ 10.98 \approx 10.98 ≈ 10.98
Variance = 10.98 / 5 ≈ 2.20 10.98 / 5 \approx 2.20 10.98/5 ≈ 2.20
Std Dev = 2.20 ≈ 1.48 \sqrt{2.20} \approx 1.48 2.20 ≈ 1.48
判定异常 :根据阈值公式:
T h r e s h o l d = M e a n + 1.5 × S t d D e v = 2.27 + ( 1.5 × 1.48 ) = 2.27 + 2.22 = 4.49 Threshold = Mean + 1.5 \times StdDev = 2.27 + (1.5 \times 1.48) = 2.27 + 2.22 = 4.49 T h res h o l d = M e an + 1.5 × St d De v = 2.27 + ( 1.5 × 1.48 ) = 2.27 + 2.22 = 4.49 然后对每个用户进行比较,发现用户 E 的距离为 4.67 > 4.49 4.67 > 4.49 4.67 > 4.49 异常点 (Anomaly) 。
(Task 4) 假设我们在研究某种植物的基因型。基因型分为四种:AA, AB, BB, O 。 由于检测技术的限制,我们无法区分 AA 和 AB ,它们在检测中都会显示为 “Type A ”。其他两种可以明确区分。我们收集了 N = 100 N=100 N = 100
观测数据 (Observed Data):
Type A (h h h
Type B (c c c
Type O (d d d
概率模型 (Probability Model): 我们将概率设为基于一个未知参数 μ \mu μ
P ( A A ) = 1 / 3 P(AA) = 1/3 P ( AA ) = 1/3 P ( A B ) = μ P(AB) = \mu P ( A B ) = μ P ( B B ) = μ P(BB) = \mu P ( BB ) = μ P ( O ) = 2 / 3 − 2 μ P(O) = 2/3 - 2\mu P ( O ) = 2/3 − 2 μ
任务: 通过 EM 算法 估算未知参数 μ \mu μ μ ( 0 ) = 0 \mu^{(0)} = 0 μ ( 0 ) = 0
根据 EM 算法,我们在迭代前需要推导出针对当前模型的递推公式。
E-Step :使用当前的 μ \mu μ AB 的数量 b b b
b = h × P ( A B ∣ Type A ) P ( A B ∣ Type A ) = P ( A B ) P ( A A ) + P ( A B ) = μ 1 / 3 + μ \begin{align*}
b = h \times P(AB | \text{Type A}) \\
P(AB | \text{Type A}) = \frac{P(AB)}{P(AA) + P(AB)} &= \frac{\mu}{1/3 + \mu}
\end{align*} b = h × P ( A B ∣ Type A ) P ( A B ∣ Type A ) = P ( AA ) + P ( A B ) P ( A B ) = 1/3 + μ μ 带入数据可以得到E-Step 公式:
b ( t ) = 43 × μ ( t ) 1 / 3 + μ ( t ) \begin{equation}
b^{(t)} = 43 \times \frac{\mu^{(t)}}{1/3 + \mu^{(t)}}
\end{equation} b ( t ) = 43 × 1/3 + μ ( t ) μ ( t ) M-Step :假设推测出的 b b b c c c d d d μ \mu μ
似然函数:
L ( μ ) = K ⋅ ( 1 / 3 ) a ⋅ ( μ ) b ⋅ ( μ ) c ⋅ ( 2 / 3 − 2 μ ) d L(\mu) = K \cdot (1/3)^a \cdot (\mu)^b \cdot (\mu)^c \cdot (2/3 - 2\mu)^d L ( μ ) = K ⋅ ( 1/3 ) a ⋅ ( μ ) b ⋅ ( μ ) c ⋅ ( 2/3 − 2 μ ) d 去对数以方便求导:
ln L = ln K + a ln ( 1 / 3 ) + ( b + c ) ln μ + d ln ( 2 / 3 − 2 μ ) \ln L = \ln K + a\ln(1/3) + (b+c)\ln\mu + d\ln(2/3 - 2\mu) ln L = ln K + a ln ( 1/3 ) + ( b + c ) ln μ + d ln ( 2/3 − 2 μ ) 对 μ \mu μ
∂ ln L ∂ μ = b + c μ − 2 d 2 / 3 − 2 μ = 0 ⟹ b + c μ = d 1 / 3 − μ ⟹ ( b + c ) ( 1 / 3 − μ ) = d μ ⟹ ( 1 / 3 ) ( b + c ) = μ ( d + b + c ) ⟹ μ = b + c 3 ( b + c + d ) \begin{align*}
&\frac{\partial \ln L}{\partial \mu} = \frac{b+c}{\mu} - \frac{2d}{2/3 - 2\mu} = 0 \\
&\implies \frac{b+c}{\mu} = \frac{d}{1/3 - \mu} \\
&\implies (b+c)(1/3 - \mu) = d\mu \\
&\implies (1/3)(b+c) = \mu(d + b + c) \\
&\implies \mu = \frac{b+c}{3(b+c+d)}
\end{align*} ∂ μ ∂ ln L = μ b + c − 2/3 − 2 μ 2 d = 0 ⟹ μ b + c = 1/3 − μ d ⟹ ( b + c ) ( 1/3 − μ ) = d μ ⟹ ( 1/3 ) ( b + c ) = μ ( d + b + c ) ⟹ μ = 3 ( b + c + d ) b + c 所以,M-Step 公式:
μ ( t + 1 ) = b ( t ) + c 3 ( b ( t ) + c + d ) \begin{equation}
\mu^{(t+1)} = \frac{b^{(t)} + c}{3(b^{(t)} + c + d)}
\end{equation} μ ( t + 1 ) = 3 ( b ( t ) + c + d ) b ( t ) + c 现在我们从 μ ( 0 ) = 0 \mu^{(0)} = 0 μ ( 0 ) = 0
下面是计算得到的表格:
轮次 (Iteration) 当前 μ ( t ) μ^{(t)} μ ( t ) E-Step: 估算 b ( t ) b^{(t)} b ( t ) M-Step: 更新 μ ( t + 1 ) μ^{(t+1)} μ ( t + 1 ) Start (0)0.0000 43 × 0 0.333 + 0 = 0 43 \times \frac{0}{0.333+0} = \mathbf{0} 43 × 0.333 + 0 0 = 0 - 1 0.0000 43 × 0.0585 0.333 + 0.0585 ≈ 6.418 43 \times \frac{0.0585}{0.333+0.0585} \approx \mathbf{6.418} 43 × 0.333 + 0.0585 0.0585 ≈ 6.418 0 + 10 3 ( 0 + 10 + 47 ) = 10 171 ≈ 0.0585 \frac{0+10}{3(0+10+47)} = \frac{10}{171} \approx \mathbf{0.0585} 3 ( 0 + 10 + 47 ) 0 + 10 = 171 10 ≈ 0.0585 2 0.0585 43 × 0.0863 0.333 + 0.0863 ≈ 8.843 43 \times \frac{0.0863}{0.333+0.0863} \approx \mathbf{8.843} 43 × 0.333 + 0.0863 0.0863 ≈ 8.843 6.418 + 10 3 ( 6.418 + 10 + 47 ) ≈ 0.0863 \frac{6.418+10}{3(6.418+10+47)} \approx \mathbf{0.0863} 3 ( 6.418 + 10 + 47 ) 6.418 + 10 ≈ 0.0863 3 0.0863 43 × 0.0954 0.333 + 0.0954 ≈ 9.568 43 \times \frac{0.0954}{0.333+0.0954} \approx \mathbf{9.568} 43 × 0.333 + 0.0954 0.0954 ≈ 9.568 8.843 + 10 3 ( 8.843 + 10 + 47 ) ≈ 0.0954 \frac{8.843+10}{3(8.843+10+47)} \approx \mathbf{0.0954} 3 ( 8.843 + 10 + 47 ) 8.843 + 10 ≈ 0.0954 4 0.0954 43 × 0.0980 0.333 + 0.0980 ≈ 9.768 43 \times \frac{0.0980}{0.333+0.0980} \approx \mathbf{9.768} 43 × 0.333 + 0.0980 0.0980 ≈ 9.768 9.568 + 10 3 ( 9.568 + 10 + 47 ) ≈ 0.0980 \frac{9.568+10}{3(9.568+10+47)} \approx \mathbf{0.0980} 3 ( 9.568 + 10 + 47 ) 9.568 + 10 ≈ 0.0980 5 0.0980 43 × 0.0989 0.333 + 0.0989 ≈ 9.823 43 \times \frac{0.0989}{0.333+0.0989} \approx \mathbf{9.823} 43 × 0.333 + 0.0989 0.0989 ≈ 9.823 9.768 + 10 3 ( 9.768 + 10 + 47 ) ≈ 0.0987 \frac{9.768+10}{3(9.768+10+47)} \approx \mathbf{0.0987} 3 ( 9.768 + 10 + 47 ) 9.768 + 10 ≈ 0.0987
从 Task 1 到 Task 4,是从 显性计算 走向 隐性推断 的过程:
我们从最直观的 文本计数 (TF-IDF) 开始;
进阶到处理海量数据的概率压缩 (MinHash );
再到寻找数据内在结构的几何划分 (K-means );
最后攻克了抽象的缺失数据参数估计 (EM )。
本章涵盖了数据挖掘中“特征提取、相似度计算、无监督学习、概率图模型”四大支柱,适合作为数据挖掘的入门。