
Introduce
先验算法 (Apriori Algorithm) 是一种用于发现频繁项集和关联规则的算法。
在学习Apriori算法之前,需要了解以下概念:
NOTE
- 项集 (Itemset):一组元素,表示一个数据集的子集。例如:
{Bread, Coke, Milk}- 支持度 (Support):表示项集在数据集中的出现频率。
- 频繁项集 (Frequent Itemset):支持度大于等于给定阈值
s的项集。- 关联规则 (Association Rule):两个项集
X和Y形如X -> Y,表示X出现,则Y也大概率出现。- 置信度 (Confidence):表示关联规则
X -> Y的概率。记作:。- 兴趣度 (Lift / Interest): 表示关联规则
X -> Y的关联程度。记作:。
下面是一个例子来理解这些概念:
想象你去超市购物,购物篮里的商品组合就是一个 项集。例如:{牛奶, 面包},{牛奶, 面包, 黄油}。
假设超市有10笔交易记录:
| 交易ID | 购买商品 |
|---|---|
| T1 | 牛奶, 面包, 黄油 |
| T2 | 牛奶, 面包 |
| T3 | 面包, 尿布, 啤酒 |
| T4 | 牛奶, 尿布, 啤酒 |
| T5 | 牛奶, 面包, 尿布, 啤酒 |
| T6 | 面包, 黄油 |
| T7 | 牛奶, 面包, 黄油 |
| T8 | 牛奶, 尿布 |
| T9 | 面包, 黄油, 啤酒 |
| T10 | 牛奶, 面包 |
我们可以计算如下项集的 支持度:
频繁项集 是指支持度 大于或等于最小支持度 阈值 s 的项集。假设我们设置最小支持度
那么频繁项集有:
{牛奶}- 支持度0.6✅{面包}- 支持度0.7✅{牛奶, 面包}- 支持度0.5✅{尿布, 啤酒}- 支持度0.3❌(不是频繁项集)
关联规则 是形如 A → B 的规则,表示 ” 如果购买了A,那么也会购买B ”。
例如:
{尿布} → {啤酒}- “买尿布的人也会买啤酒”{牛奶, 黄油} → {面包}- “买牛奶和黄油的人也会买面包”
我们用 置信度 来表示在购买了A的条件下,同时购买B的概率。
例如,对于规则 {尿布} → {啤酒}:
而 兴趣度 用来衡量A和B之间关联的强度,判断它们是否真正相关,还是仅仅是偶然。
例如,对于规则 {牛奶} → {面包}:
我们一般认为:
- :A和B独立,没有关联
- :正相关(购买A增加了购买B的可能性)
- :负相关(购买A降低了购买B的可能性)
我们今天要介绍的Apriori算法,主要用于发现大型数据集中的 频繁项集和关联规则。
Principle
Apriori 算法的核心思想是:如果一个项集是频繁的,那么它的所有子集也一定是频繁的。
因此,我们可以得到该命题的逆否命题:如果一个项集不是频繁的,那么它的所有超集也不是频繁的。
例如:用户不想购买 {泡面},所以用户也不想购买 {泡面, 火腿}。
Apriori 算法将递归地生成所有可能的项集,并使用支持度来判断项集的频繁性。对于集合而言,一个长度为 的项集的子集一共有 个,其中,非空的子集有 个。
需要找到所有的项集,我们需要从长度 1 的项集开始,到长度为 的项集结束。这样搜索的过程就像 广度优先搜索 一样。
接下来,我们通过一个例子一步步推演 Apriori 算法的步骤:
假设有如下的数据集:
| TID | 商品列表 |
|---|---|
| T1 | I1, I2, I5 |
| T2 | I2, I4 |
| T3 | I2, I3 |
| T4 | I1, I2, I4 |
| T5 | I1, I3 |
| T6 | I2, I3 |
| T7 | I1, I3 |
| T8 | I1, I2, I3, I5 |
| T9 | I1, I2, I3 |
其中:
- 总交易数:
- 最小支持度:
- 第一轮:找到所有的频繁 1-项集
L1
我们首先生成候选 1-项集 C1。
扫描数据库,统计每个商品出现次数:
| 项集 | Support |
|---|---|
| {I1} | 6 |
| {I2} | 7 |
| {I3} | 6 |
| {I4} | 2 |
| {I5} | 2 |
通过我们的 min_sup 过滤得到频繁 1-项集 L1。因为最小支持度计数 = 2,所有项集都满足!
所以:
L1 = ({I1}, {I2}, {I3}, {I4}, {I5})
此时,第一轮得到的频繁项集个数 .
- 第二轮:找到所有的频繁 2-项集
L2
同样的,我们首先生成候选 2-项集 C2。我们需要 基于第一次频繁项集,找出第二次候选集。
个商品两两组合,可以得到 个候选项集。于是对每个组合计算其支持度,可以得到:
| 项集 | 出现的交易 | 支持度计数 |
|---|---|---|
| {I1, I2} | T1, T4, T8, T9 | 4 ✅ |
| {I1, I3} | T5, T7, T8, T9 | 4 ✅ |
| {I1, I4} | T4 | 1 ❌ |
| {I1, I5} | T1, T8 | 2 ✅ |
| {I2, I3} | T3, T6, T8, T9 | 4 ✅ |
| {I2, I4} | T2, T4 | 2 ✅ |
| {I2, I5} | T1, T8 | 2 ✅ |
| {I3, I4} | - | 0 ❌ |
| {I3, I5} | T8 | 1 ❌ |
| {I4, I5} | - | 0 ❌ |
经过 min_sup 过滤,我们得到频繁 2-项集 L2。
L2 = ({I1, I2}, {I1, I3}, {I1, I5}, {I2, I3}, {I2, I4}, {I2, I5})
此时,第二轮得到的频繁项集个数 .
- 第三轮:找到所有的频繁 3-项集
L3
同样的,我们由 L2 生成候选3-项集 C3,可以得到 个候选项集。
但是根据我们的算法核心思想:频繁项集的子集也是频繁的,所以,我们只需要考虑 L2 的超集。
运用自连接 (两个k-1-项集,如果它们前k-2个项相同,则可以连接) 的方法,可以找到 L2 的超集:
{I1, I2} ⨝ {I1, I3} → {I1, I2, I3}{I1, I2} ⨝ {I1, I5} → {I1, I2, I5}{I1, I3} ⨝ {I1, I5} → {I1, I3, I5}{I2, I3} ⨝ {I2, I4} → {I2, I3, I4}{I2, I3} ⨝ {I2, I5} → {I2, I3, I5}{I2, I4} ⨝ {I2, I5} → {I2, I4, I5}
但是这样得到的超集并不能说明超集的所有的子集都是频繁的,所以我们需要进行 剪枝 —— 即检查每个候选项集的所有2-项子集是否都在L2中:
{I1, I2, I3}:子集:{I1, I2}✓, {I1, I3}✓, {I2, I3}✓→ 保留{I1, I2, I5}:子集:{I1, I2}✓, {I1, I5}✓, {I2, I5}✓→ 保留{I1, I3, I5}:子集:{I1, I3}✓, {I1, I5}✓, {I3, I5}❌→ 剪枝!{I2, I3, I4}:子集:{I2, I3}✓, {I2, I4}✓, {I3, I4}❌→ 剪枝!{I2, I3, I5}:子集:{I2, I3}✓, {I2, I5}✓, {I3, I5}❌→ 剪枝!{I2, I4, I5}:子集:{I2, I4}✓, {I2, I5}✓, {I4, I5}❌→ 剪枝!
剪枝后的 C3:
C3 = ({I1, I2, I3}, {I1, I2, I5}
接下来依旧计算其支持度:
| 项集 | 出现的交易 | 支持度计数 |
|---|---|---|
| {I1, I2, I3} | T8, T9 | 2 ✅ |
| {I1, I2, I5} | T1, T8 | 2 ✅ |
所有可以得到 频繁 3-项集 L3:
L3 = ({I1, I2, I3}, {I1, I2, I5})
此时,第三轮得到的频繁项集个数 .
- 第四轮:找到所有的频繁 4-项集
L4
还是由 L3 生成候选4-项集 C4。L3 只有2个项集,于是它的自连接结果:{I1, I2, I3} ⨝ {I1, I2, I5} → {I1, I2, I3, I5}
同样的进行剪枝,判断4-项集的子集是否都在 L3 中:
{I1, I2, I3, I5}: 子集 {I1, I2, I3}✓, {I1, I2, I5}✓, {I1, I3, I5}❌, {I2, I3, I5}❌ → 剪枝!
此时候选项集 C4 为空,无法生成更多频繁项集,算法结束。
- 于是,综合上述每一轮得到的频繁项集,可以得到:
| 项集大小 | 项集 | 支持度计数 |
|---|---|---|
| 1 | {I1} | 6 |
| 1 | {I2} | 7 |
| 1 | {I3} | 6 |
| 1 | {I4} | 2 |
| 1 | {I5} | 2 |
| 2 | {I1, I2} | 4 |
| 2 | {I1, I3} | 4 |
| 2 | {I1, I5} | 2 |
| 2 | {I2, I3} | 4 |
| 2 | {I2, I4} | 2 |
| 2 | {I2, I5} | 2 |
| 3 | {I1, I2, I3} | 2 |
| 3 | {I1, I2, I5} | 2 |
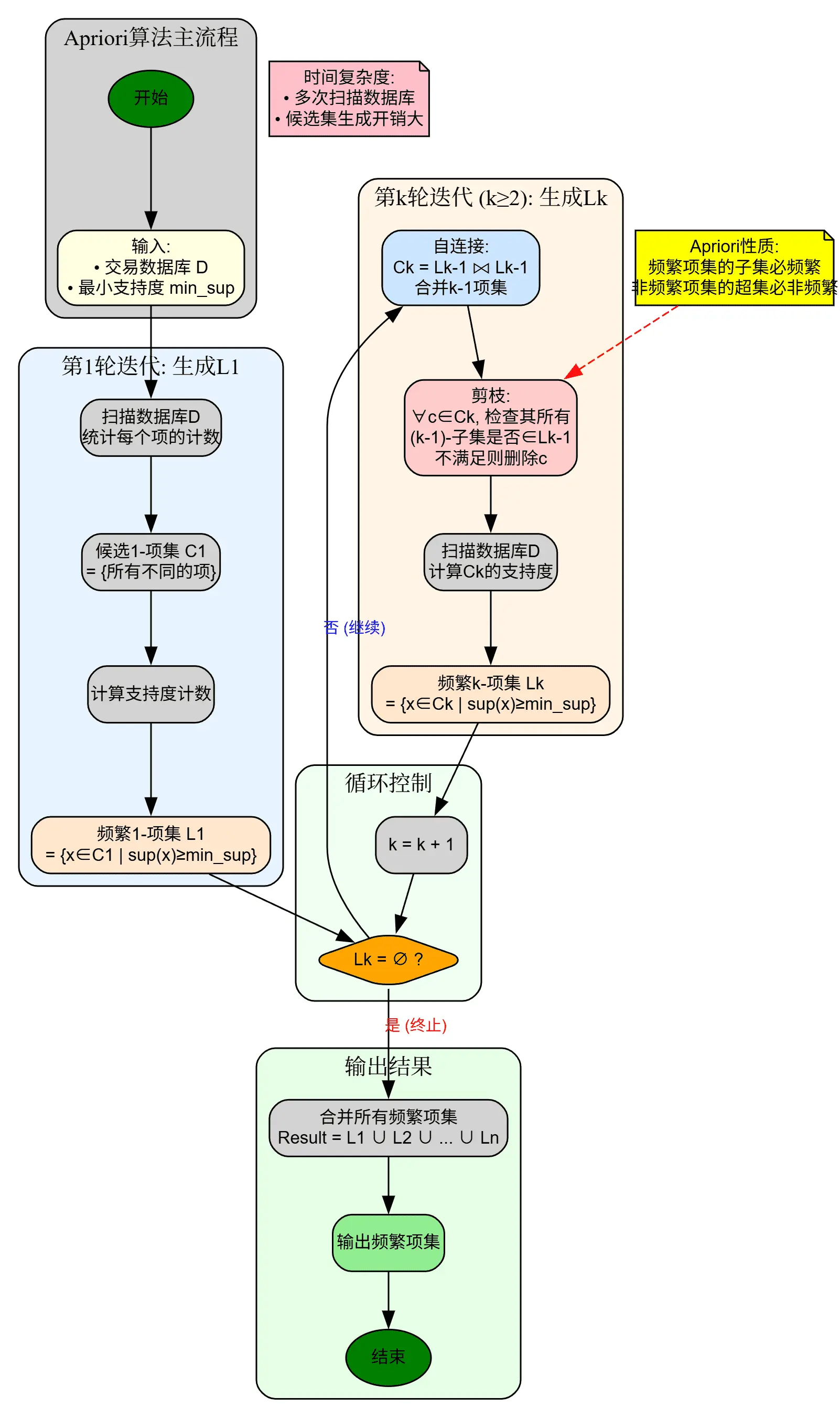
总结一下 Apriori 算法的过程,如下流程图所示:
Code
我们可以使用 Python 实现 Apriori 算法:
- 数据准备:
我们将数据集保存在 ./data.csv 中,并进行数据结构的初始化:
数据形如:
| node1 | node2 |
|---|---|
| 0 | 1838 |
| 0 | 1009 |
| 2 | 1744 |
| 3 | 14 |
| 4 | 2543 |
import csv
def processing_data(): with open("./data.csv") as csvfile: data = list(csv.reader(csvfile))
dic = {} for i in data[1:]: # 跳过表头 if not i[0] in dic: dic[i[0]] = [i[1]] # 创建新的交易 else: dic[i[0]].append(i[1]) # 添加商品到已有交易 data_set = list(dic.values()) return data_set
data_set = processing_data()处理后可以得到数据形如:
data_set = [['1838', '1009'], ['1744'], ['14'], ['2543']]
- 创建候选 1-项集
C1:
我们需要从所有事务中,找出所有唯一的物品,并生成候选 1-项集 C1:
def create_C1(data_set): C1 = set() for t in data_set: for item in t: item_set = frozenset([item]) C1.add(item_set) return C1这里使用了 set() 去重,frozenset() 用于创建不可变集合。
这一步可以得到候选 1-项集 C1 形如:
C1 = {frozenset({'1838'}), frozenset({'1009'}), frozenset({'1744'}), frozenset({'14'}), frozenset({'2543'})}
- 检验是否满足Apriori性质:
在第一轮时,不需要进行剪枝,因为不存在上一轮的结果。而在之后的轮次中,我们生成候选项集 C_k 时需要 先验证候选项集的子集是否都在上一轮生成的频繁项集中。
我们可以写如下的验证函数:
def is_apriori(Ck_item, Lksub1): for item in Ck_item: sub_Ck = Ck_item - frozenset([item]) # 生成(k-1)项子集 if sub_Ck not in Lksub1: # 检查子集是否在Lk-1中 return False return True其中,Ck_item 为待验证的候选项集,Lksub1 为上一轮生成的频繁项集。它的过程如下:
- 生成 Ck_item 的所有 (k-1) 项子集
- 检查每个子集是否都在 Lksub1 中
- 如果有任何子集不频繁,则该候选项集不满足Apriori性质
- 创建候选 k-项集
Ck:
创建候选 k-项集 Ck 需要依赖上一次生成的频繁项集 Lksub1,于是我们可以对频繁项集 Lksub1 进行自连接,生成候选 k-项集 Ck.
它的过程如下:
- 自连接 (Self-Join):将
Lksub1中的项集两两合并 - 条件判断:只有当两个
(k-1)-项集前(k-2)个元素相同时才连接 - 剪枝 (Prune):利用
is_apriori函数过滤不满足Apriori性质的候选
def create_Ck(Lksub1, k): Ck = set() list_Lksub1 = list(Lksub1)
for i in range(len(list_Lksub1)): for j in range(i + 1, len(list_Lksub1)): # 获取两个(k-1)-项集 l1 = list(list_Lksub1[i]) l2 = list(list_Lksub1[j])
# 排序,确保比较的一致性 l1.sort() l2.sort()
# 只有前(k-2)个元素相同时才能连接 if l1[0:k-2] == l2[0:k-2]: # 合并生成候选k-项集 Ck_item = list_Lksub1[i] | list_Lksub1[j]
if is_apriori(Ck_item, Lksub1): Ck.add(Ck_item)
return Ck
- 创建频繁 k-项集
Lk:
根据上一步可以得到候选 k-项集 Ck,然后根据支持度进行过滤,得到频繁 k-项集 Lk。
def generate_Lk_by_Ck(data_set, Ck, min_support, support_data): # 初始化每个候选项集的支持度计数 Ck_count = {} for item in Ck: Ck_count[item] = 0
# 扫描数据集,统计每个候选项集的出现次数 for transaction in data_set: transaction_set = set(transaction)
# 检查每个候选项集 for item in Ck: # 如果候选项集是交易的子集,计数+1 if item.issubset(transaction_set): Ck_count[item] += 1
# 初始化频繁k-项集 Lk = set()
# 遍历每个候选项集,根据支持度筛选 for item in Ck: support = float(Ck_count[item]) / float(len(data_set)) support_data[item] = support
if support >= min_support: Lk.add(item)
return Lk参数说明:
| 参数 | 类型 | 说明 |
|---|---|---|
data_set | list | 交易数据集,如 [['I1','I2'], ['I2','I3'], ...] |
Ck | set | 候选k-项集集合,如 {frozenset({'I1','I2'}), ...} |
min_support | float | 最小支持度阈值,如 0.22 (22%) |
support_data | dict | 用于存储项集支持度的字典(会被修改) |
- 包装函数计算频繁项集
L:
我们可以将上述关键的步骤封装到一个函数中,得到频繁项集 L。它的完整过程如下:
- 生成候选1-项集
C1 - 从
C1生成频繁1-项集L1 - 循环生成
L2, L3, ..., Lk:- 由
L(i-1)生成候选Ci - 从
Ci生成频繁Li - 如果
Li为空,提前终止
- 由
- 返回所有频繁项集列表
L和支持度字典support_data
def generate_L(data_set, k, min_support): # 初始化支持度字典 support_data = {}
# Step 1: 生成候选1-项集 C1 C1 = create_C1(data_set)
# Step 2: 从 C1 生成频繁1-项集 L1 L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
L = [L1]
# Step 3: 迭代生成 L2, L3, ..., Lk for i in range(2, k + 1): Ci = create_Ck(L[i-2], i)
# 如果候选集为空,终止 if len(Ci) == 0: break
Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
# 如果频繁项集为空,终止 if len(Li) == 0: break
L.append(Li)
return L, support_data至此,我们的Apriori算法的各个步骤以及完成,下面是一个整体的调用示例:
data_set = [ ['I1', 'I2', 'I5'], ['I2', 'I4'], ['I2', 'I3'], ['I1', 'I2', 'I4'], ['I1', 'I3'], ['I2', 'I3'], ['I1', 'I3'], ['I1', 'I2', 'I3', 'I5'], ['I1', 'I2', 'I3'],]
print("=" * 80)print("数据集展示")print("=" * 80)for idx, trans in enumerate(data_set, 1): print(f" T{idx}: {trans}")print()# 调用函数生成频繁项集L, support_data = generate_L(data_set, k=3, min_support=0.2)
print("\n" + "=" * 80)print("频繁项集结果")print("=" * 80)for idx, lk in enumerate(L, 1): print(f"\n【频繁{idx}-项集 L{idx}】(共 {len(lk)} 个)") print("-" * 80)
# 按支持度排序 sorted_lk = sorted(lk, key=lambda x: support_data[x], reverse=True)
for item in sorted_lk: support = support_data[item] count = int(support * len(data_set)) items_str = str(set(item)) print(f" {items_str:25s} | 支持度: {support:.3f} ({support*100:5.1f}%) | 计数: {count}")此外,我们还可以在生成频繁项集的基础上,生成关联规则。它依赖置信度这个指标,算法可以这么设计:
对于每个频繁项集 Lk:
- 生成所有可能的规则划分,例如:
{I1, I2, I3} → [{I1}→{I2,I3}, {I2}→{I1,I3}, ...]生成的规则有 个 (真子集)。 - 对于每个规则 A → B:
- 计算置信度
- 如果置信度 则该规则是需要保留的关联规则。
from itertools import combinations
def generate_big_rules(L, support_data, min_conf): big_rule_list = []
# 从L2开始遍历(L1不能生成规则) for i in range(1, len(L)): for itemset in L[i]: # 生成该项集的所有可能规则 rules = generate_rules_from_itemset( itemset, support_data, min_conf )
# 将满足条件的规则添加到结果中 big_rule_list.extend(rules)
return big_rule_list
def generate_rules_from_itemset(itemset, support_data, min_conf): rules = [] itemset_support = support_data[itemset]
# 枚举所有可能的前件大小(从1到len-1) for i in range(1, len(itemset)): for antecedents in combinations(itemset, i): # 获取真子集 antecedent = frozenset(antecedents)
# 后件 = 项集 - 前件 consequent = itemset - antecedent
# 检查前件是否在support_data中(必须是频繁项集) if antecedent in support_data: # 计算置信度 conf = float(itemset_support) / float(support_data[antecedent])
# 如果置信度满足要求,添加规则 if conf >= min_conf: rules.append((antecedent, consequent, conf))
return rules我们在这个基础上,还可以增加有趣度的判断:
def generate_rules_from_itemset(itemset, support_data, min_conf, calculate_lift=True): rules = [] itemset_support = support_data[itemset]
for i in range(1, len(itemset)): for antecedent_tuple in combinations(itemset, i): antecedent = frozenset(antecedent_tuple) consequent = itemset - antecedent
if antecedent in support_data and consequent in support_data: # 计算置信度 conf = float(itemset_support) / float(support_data[antecedent])
if conf >= min_conf: if calculate_lift: # 计算有趣度 lift = float(itemset_support) / ( float(support_data[antecedent]) * float(support_data[consequent]) ) rules.append((antecedent, consequent, conf, lift)) else: rules.append((antecedent, consequent, conf))
return rulesSummary
Apriori 算法基于 “频繁项集的所有子集也必须是频繁的” 这一核心原理,找到所有频繁项集,并生成关联规则。
它采用自底向上的方式,从1-项集开始,逐层生成并验证k-项集,形成类似广度优先的搜索过程。
它还通过剪枝策略 —— 删除子集不在上一层频繁项集的候选项集,大幅减少候选项集数量。

