分治法 / Divide-and-Conquer# 当一个问题足够大,且可以分解为若干个和当前问题形式一致的子问题时,我们可以使用递归的方法去求解它。我们通常使用如下三步去求解这样的递归问题 (recursive case):
分解 (Divide) : 将原问题分解为若干子问题,形式与原问题一致,但规模更小。解决 (Conquer) : 递归求解子问题。合并 (Combine) : 将子问题的解合并为原问题的解。 我们可以用一系列函数符号来表示递归的通式,于是我们得到了递归式的定义:
Definition - Recurrence A recurrence is an equation that describes a function in terms of its value on other, typically smaller, arguments.
递归式 (recurrence) 是一个通过函数在较小的参数上的取值来描述一个函数的等式。
通过递归式的定义,我们可以使用数学方法去描述分治算法运行时间。
Definition - Algorithmic Recurrences 对于一个算法,它的递归式 T ( n ) T(n) T ( n ) n 0 > 0 n_0 > 0 n 0 > 0
对于所有 n < n 0 n < n_0 n < n 0 T ( n ) = Θ ( 1 ) T(n) = \Theta(1) T ( n ) = Θ ( 1 )
对于所有 n ≥ n 0 n \ge n_0 n ≥ n 0
于是,估计分治算法的运行时间转换成了解递归式的边界。教科书中提供了四种方法去解递归式:
代入法 / Substitution method : 使用 数学归纳法 去猜测递归式的边界,并通过推导去证明。递归树法 / Recursion-tree method : 将递归式转化为递归树,计算不同层次结点递归的代价去计算递归式的边界。主方法 / Master method : 通过主方法,将递归式中的参数替换为实际参数的值,并求解。Akra-Bazzi方法 : 通过微积分的方法处理更为通用且复杂的递归式。该方法是主方法的一般形式,在本章中不会过多介绍。 代入法 / Substitution method# 代入法 (Substitution method) 是使用数学归纳法去猜测递归式边界,并通过推导去证明。它的基本思路是:
使用常数符号去猜测递归式 T ( n ) T(n) T ( n )
使用数学归纳法求出解中的常数,并证明解的正确。
无渐进符号递归式# 我们通过如下一个例子来展示代入法的过程:
T ( n ) = { 1 if n = 1 , 2 T ( n / 2 ) + n if n > 1. T(n) = \begin{cases}
1 & \text{if } n = 1,
\\ 2T(n/2) + n & \text{if } n > 1.
\end{cases} T ( n ) = { 1 2 T ( n /2 ) + n if n = 1 , if n > 1. 我们把 n = 1 n = 1 n = 1 T ( n ) T(n) T ( n ) T ( 1 ) = 1 T(1) = 1 T ( 1 ) = 1
因为递归式很多情况下与对数函数有紧密关系,我们可以猜测 T ( n ) = n lg ( n ) + n T(n) = n\lg(n) + n T ( n ) = n lg ( n ) + n
应用数学归纳法:
当 n = 1 n = 1 n = 1 T ( 1 ) = 1 lg ( 1 ) + 1 = 1 T(1) = 1\lg(1) + 1 = 1 T ( 1 ) = 1 lg ( 1 ) + 1 = 1
当 n > 1 n > 1 n > 1 T ( n / 2 ) = ( n / 2 ) lg ( n / 2 ) + n / 2 T(n/2) = (n/2) \lg(n/2) + n/2 T ( n /2 ) = ( n /2 ) lg ( n /2 ) + n /2 T ( n ) T(n) T ( n ) T ( n ) = 2 T ( n / 2 ) + n = 2 [ ( n / 2 ) lg ( n / 2 ) + n / 2 ] + n = [ n lg ( n / 2 ) + n ] + n = [ n lg ( n ) − n lg ( 2 ) + n ] + n = n lg ( n ) + n \begin{align*}
T(n) &= 2T(n/2) + n \\
&= 2[(n/2) \lg(n/2) + n/2] + n \\
&= [n \lg(n/2) + n] + n \\
&= [n \lg(n) - n \lg(2) + n] + n \\
&= n \lg(n) + n
\end{align*} T ( n ) = 2 T ( n /2 ) + n = 2 [( n /2 ) lg ( n /2 ) + n /2 ] + n = [ n lg ( n /2 ) + n ] + n = [ n lg ( n ) − n lg ( 2 ) + n ] + n = n lg ( n ) + n
带有渐进符号的递归式# 然而,猜测成功是代入法非常关键的一步,如果我们要解这样如下的递归式:
T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n) = 2T(n/2) + \Theta(n) T ( n ) = 2 T ( n /2 ) + Θ ( n )
你也许会无从猜测它的形式,因为它带有 Θ ( n ) \Theta(n) Θ ( n )
对于上述递归式,我们可以 用 c n cn c n (因为 c n cn c n Θ ( n ) \Theta(n) Θ ( n ) c c c
当我们求解该递归式的上界的时候,即求解:T ( n ) ≤ 2 T ( n / 2 ) + c n T(n) \le 2T(n/2) + cn T ( n ) ≤ 2 T ( n /2 ) + c n
我们可以继续运用代入法,只是从等式变成了不等式,猜测 T ( n ) ≤ d n lg ( n ) T(n) \le dn\lg(n) T ( n ) ≤ d n lg ( n ) d d d
和之前一样,对它进行数学归纳法证明:
当 n = 1 n=1 n = 1 T ( n ) ≤ d l g 1 = 0 T(n) \le d\ lg1= 0 T ( n ) ≤ d l g 1 = 0 T ( n ) T(n) T ( n )
当 n > 1 n>1 n > 1 T ( n / 2 ) ≤ d ( n / 2 ) lg ( n / 2 ) T(n/2) \le d (n/2) \lg(n/2) T ( n /2 ) ≤ d ( n /2 ) lg ( n /2 ) T ( n ) T(n) T ( n )
T ( n ) ≤ 2 T ( n / 2 ) + c n = 2 [ d ( n / 2 ) lg ( n / 2 ) ] + c n = [ d n lg ( n ) − d n lg ( 2 ) ] + c n = d n lg ( n ) − d n + c n ≤ d n lg ( n ) if (- dn + cn) ≤ 0 d ≥ c \begin{align*}
T(n) &\le 2T(n/2) + cn \\
&= 2[d(n/2)\lg(n/2)] + cn \\
&= [dn\lg(n) - dn\lg(2)] + cn \\
&= dn\lg(n) - dn + cn \\
&\le dn\lg(n) & \text{if (- dn + cn)} \le 0 \\
& & d \ge c
\end{align*} T ( n ) ≤ 2 T ( n /2 ) + c n = 2 [ d ( n /2 ) lg ( n /2 )] + c n = [ d n lg ( n ) − d n lg ( 2 )] + c n = d n lg ( n ) − d n + c n ≤ d n lg ( n ) if (- dn + cn) ≤ 0 d ≥ c 那么我们可以说,当 d ≥ c d \ge c d ≥ c T ( n ) ≤ d n lg ( n ) T(n) \le dn\lg(n) T ( n ) ≤ d n lg ( n ) T ( n ) T(n) T ( n ) T ( n ) = O ( n lg n ) T(n) = O(n\lg n) T ( n ) = O ( n lg n )
同理我们还可以证明其下界,用 T ( n ) ≥ 2 T ( n / 2 ) + c n T(n) \ge 2T(n/2) + cn T ( n ) ≥ 2 T ( n /2 ) + c n T ( n ) ≥ d n lg n T(n) \ge dn\lg n T ( n ) ≥ d n lg n T ( n ) = Ω ( n lg n ) T(n) = \Omega(n\lg n) T ( n ) = Ω ( n lg n )
于是我们可以得到 T ( n ) = Θ ( n lg n ) T(n) = \Theta(n\lg n) T ( n ) = Θ ( n lg n )
需要减去低阶项的递归式# 你也许会发现,有时已经正确猜测出渐进边界,但是无法通过数学归纳法去证明,例如:
T ( n ) = 2 T ( n / 2 ) + Θ ( 1 ) T(n) = 2T(n/2) + \Theta(1) T ( n ) = 2 T ( n /2 ) + Θ ( 1 )
我们可以猜测它的上界是 T ( n ) = O ( n ) T(n) = O(n) T ( n ) = O ( n )
像之前一样应用数学归纳法, 尝试证明对于某个恰当的参数 c c c T ( n ) ≤ 2 T ( n / 2 ) + Θ ( 1 ) T(n) \le 2T(n/2) + \Theta(1) T ( n ) ≤ 2 T ( n /2 ) + Θ ( 1 ) T ( n ) ≤ c n T(n) \le cn T ( n ) ≤ c n
当 n = 1 n=1 n = 1 T ( n ) ≤ c T(n) \le c T ( n ) ≤ c T ( n ) T(n) T ( n )
当 n > 1 n>1 n > 1 T ( n / 2 ) ≤ c ( n / 2 ) T(n/2) \le c(n/2) T ( n /2 ) ≤ c ( n /2 ) T ( n ) T(n) T ( n )
T ( n ) ≤ 2 T ( n / 2 ) + Θ ( 1 ) = 2 [ c ( n / 2 ) ] + Θ ( 1 ) = c n + Θ ( 1 ) \begin{align*}
T(n) &\le 2T(n/2) + \Theta(1) \\
&= 2[c(n/2)] + \Theta(1) \\
&= cn + \Theta(1)
\end{align*} T ( n ) ≤ 2 T ( n /2 ) + Θ ( 1 ) = 2 [ c ( n /2 )] + Θ ( 1 ) = c n + Θ ( 1 ) 此时我们会发现,好像不存在什么参数的取值能使不等式配平为 T ( n ) ≤ c n T(n) \le cn T ( n ) ≤ c n Θ ( 1 ) \Theta(1) Θ ( 1 )
因此,我们可以尝试利用待定系数法的思想,减去一个低阶项 。我们的新猜测为:T ( n ) ≤ c n − d T(n) \le cn - d T ( n ) ≤ c n − d d d d Θ ( 1 ) \Theta(1) Θ ( 1 )
再次尝试数学归纳法:
当 n = 1 n=1 n = 1 T ( n ) ≤ c − d T(n) \le c - d T ( n ) ≤ c − d T ( n ) T(n) T ( n )
当 n > 1 n>1 n > 1 T ( n / 2 ) ≤ c ( n / 2 ) − d T(n/2) \le c(n/2) - d T ( n /2 ) ≤ c ( n /2 ) − d T ( n ) T(n) T ( n )
T ( n ) ≤ 2 T ( n / 2 ) + Θ ( 1 ) = 2 [ c ( n / 2 ) − d ] + Θ ( 1 ) = c n − 2 d + Θ ( 1 ) = c n − d + ( − d + Θ ( 1 ) ) ≤ c n − d if ( − d + Θ ( 1 ) ) ≤ 0 d ≥ Θ ( 1 ) \begin{align*}
T(n) &\le 2T(n/2) + \Theta(1) \\
&= 2[c(n/2) - d] + \Theta(1) \\
&= cn - 2d + \Theta(1) \\
&= cn - d + (-d + \Theta(1)) \\
&\le cn - d & \text{if } (-d + \Theta(1)) \le 0 \\
& & d \ge \Theta(1)
\end{align*} T ( n ) ≤ 2 T ( n /2 ) + Θ ( 1 ) = 2 [ c ( n /2 ) − d ] + Θ ( 1 ) = c n − 2 d + Θ ( 1 ) = c n − d + ( − d + Θ ( 1 )) ≤ c n − d if ( − d + Θ ( 1 )) ≤ 0 d ≥ Θ ( 1 ) 那我们就可以说,当 d d d Θ ( 1 ) \Theta(1) Θ ( 1 ) T ( n ) ≤ c n − d T(n) \le cn - d T ( n ) ≤ c n − d T ( n ) = O ( n ) T(n) = O(n) T ( n ) = O ( n )
常见错误# 我们证明的时候可能会出现一些常见的问题,例如:T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n) = 2T(n/2) + Θ(n) T ( n ) = 2 T ( n /2 ) + Θ ( n ) T ( n ) = O ( n ) T(n) = O(n) T ( n ) = O ( n )
直接带入渐进符号 :T ( n ) ≤ 2 O ( n / 2 ) + Θ ( n ) = 2 O ( n ) + Θ ( n ) ≠ O ( n ) T(n) \le 2\ O(n/2) + \Theta(n) = 2\ O(n) + \Theta(n) \not = O(n) T ( n ) ≤ 2 O ( n /2 ) + Θ ( n ) = 2 O ( n ) + Θ ( n ) = O ( n ) O ( n ) O(n) O ( n ) 无法确定 Θ ( n ) \Theta(n) Θ ( n ) c c c 。不替换渐进符号 :T ( n ) ≤ 2 c ( n / 2 ) + Θ ( n ) = c n + Θ ( n ) ≠ O ( n ) T(n) \le 2c(n/2) + Θ(n) = cn + \Theta(n) \not = O(n) T ( n ) ≤ 2 c ( n /2 ) + Θ ( n ) = c n + Θ ( n ) = O ( n ) 并非证明出与归纳假设严格一致的形式 T ( n ) ≤ c n T(n) \le cn T ( n ) ≤ c n T ( n ) ≤ c n T(n) \le cn T ( n ) ≤ c n 。 递归树法 / Recursion-tree method# 使用代入法正确猜测递归式的边界可能比较困难,但是递归树方法 (Recursion-tree method) 却可以解决这个问题。对于递归式求解问题,我们大多数都可以使用递归树方法计算做出猜测,最后使用代入法去验证。
在递归树中,每个结点表示一个单一子问题的代价(需要时间) ,子问题对应某次递归函数的调用。我们将树中每层中的代价求和,得到每层代价,然后将所有层的代价求和,得到所有层次递归调用的总代价。
递归树方法 (Recursion-tree method) 的基本思路是:
构建递归树: 将递归式转换成递归树。
计算递归树中代价:计算递归树中每层的代价、树的高度。
代价求和:将每层的代价求和,得到所有层代价的总和,即为递归函数的总运行时间。
我们通过一个例子来演示递归树法的过程:
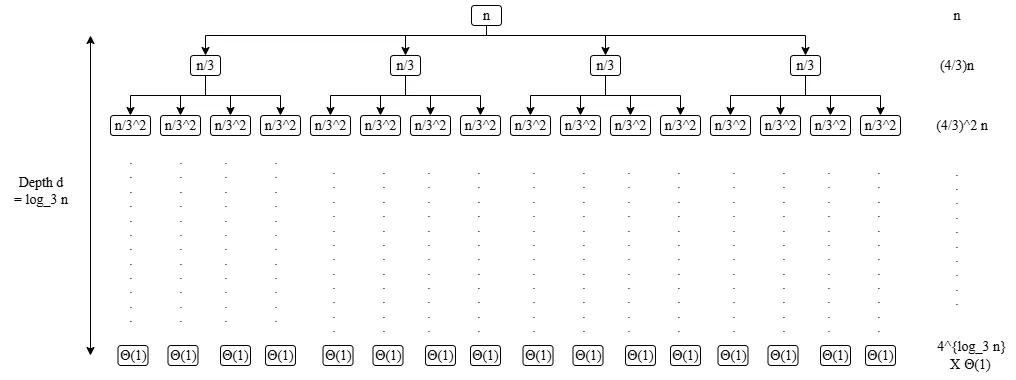
T ( n ) = 3 T ( n / 4 ) + Θ ( n 2 ) T(n) = 3T(n/4) + \Theta(n^2) T ( n ) = 3 T ( n /4 ) + Θ ( n 2 )
我们用 c n 2 cn^2 c n 2 Θ ( n 2 ) \Theta(n^2) Θ ( n 2 ) c c c T ( n ) = 3 T ( n / 4 ) + c n 2 T(n) = 3T(n/4) + cn^2 T ( n ) = 3 T ( n /4 ) + c n 2
构建递归树:根节点中的 c n 2 cn^2 c n 2 n / 4 n/4 n /4
因为我们递归有3个,故从 T ( n ) T(n) T ( n )
T ( n / 4 ) T(n/4) T ( n /4 ) T ( n ) = 3 T ( n / 4 ) + c n 2 T(n) = 3T(n/4) + cn^2 T ( n ) = 3 T ( n /4 ) + c n 2 T ( n / 4 ) = 3 T ( n / 16 ) + c n 2 T(n/4) = 3T(n/16) + cn^2 T ( n /4 ) = 3 T ( n /16 ) + c n 2 T ( n / 4 ) T(n/4) T ( n /4 )
同理我们可以继续分 T ( n / 16 ) T(n/16) T ( n /16 )
递归树中代价的计算:
观察递归树,我们可以计算每层 (用深度来表示以匹配指数, 根结点的深度为 0) 的代价:
第1层的代价:c ( n / 4 ) 2 × 3 = 3 c ( n / 4 ) 2 = ( 3 / 4 2 ) c n 2 c(n/4)^2 \times 3 = 3c(n/4)^2 = (3/4^2)\ cn^2 c ( n /4 ) 2 × 3 = 3 c ( n /4 ) 2 = ( 3/ 4 2 ) c n 2
第2层的代价:c ( n / 16 ) 2 × 9 = 9 c ( n / 16 ) 2 = ( 3 / 4 2 ) 2 c n 2 c(n/16)^2 \times 9 = 9c(n/16)^2 = (3/4^2)^2\ cn^2 c ( n /16 ) 2 × 9 = 9 c ( n /16 ) 2 = ( 3/ 4 2 ) 2 c n 2
第3层的代价:c ( n / 64 ) 2 × 27 = 27 c ( n / 64 ) 2 = ( 3 / 4 2 ) 3 c n 2 c(n/64)^2 \times 27 = 27c(n/64)^2 = (3/4^2)^3\ cn^2 c ( n /64 ) 2 × 27 = 27 c ( n /64 ) 2 = ( 3/ 4 2 ) 3 c n 2
可以推广到第i层的代价:c ( n / 4 i ) 2 × 3 i = ( 3 / 4 2 ) i c n 2 c(n/4^i)^2 \times 3^i = (3/4^2)^i\ cn^2 c ( n / 4 i ) 2 × 3 i = ( 3/ 4 2 ) i c n 2
这样的规律可以一直推广到第 h - 1 层,h 为递归树的总深度。而最后一层的代价则可以通过 最后一层的节点数量 × Θ ( 1 ) \times\ \Theta(1) × Θ ( 1 )
接下来我们可以通过递归树中节点的规模来计算递归树的深度 h h h
观察递归树可以知道,每个子结点规模为父结点的 1 / 4 1/4 1/4
第1层的子结点规模为 ( n / 4 ) 2 = ( n / 4 1 ) 2 (n/4)^2 = (n/4^1)^2 ( n /4 ) 2 = ( n / 4 1 ) 2
第2层的子结点规模为 ( n / 16 ) 2 = ( n / 4 2 ) 2 (n/16)^2 = (n/4^2)^2 ( n /16 ) 2 = ( n / 4 2 ) 2
第3层的子结点规模为 ( n / 64 ) 2 = ( n / 4 3 ) 2 (n/64)^2 = (n/4^3)^2 ( n /64 ) 2 = ( n / 4 3 ) 2
可以推广到第i层的子结点规模:( n / 4 i ) 2 (n/4^i)^2 ( n / 4 i ) 2 1 1 1
于是,在最后一层拥有的子节点规模:
( n / 4 h ) 2 = 1 ⟹ n / 4 h = 1 ⟹ h = log 4 n \begin{align*}
&(n/4^h)^2 = 1 \\
\implies& n/4^h = 1 \\
\implies& h = \log_4 n
\end{align*} ⟹ ⟹ ( n / 4 h ) 2 = 1 n / 4 h = 1 h = log 4 n 我们得到递归树的深度 h = log 4 n h = \log_4 n h = log 4 n
有了深度的表达式后,可以得出第0层到第h - 1层的代价表达式。要计算总代价,我们还需要最后一层的节点数量才能计算最后一层的代价。
观察递归树每层的节点数量,可以发现:
第0层的节点数量:1 = 3 0 1 = 3^0 1 = 3 0
第1层的节点数量:3 = 3 1 3 = 3^1 3 = 3 1
第2层的节点数量:9 = 3 2 9 = 3^2 9 = 3 2
第3层的节点数量:27 = 3 3 27 = 3^3 27 = 3 3
在第 i 层,节点数量为 3 i 3^i 3 i 3 h = 3 log 4 n 3^{h} = 3^{\log_4 n} 3 h = 3 l o g 4 n
所以最后一层的代价为:3 log 4 n × Θ ( 1 ) 3^{\log_4 n} \times \Theta(1) 3 l o g 4 n × Θ ( 1 )
代价求和:
我们可以发现,在第0层到第h - 1层,代价是一个等比数列:
第0层的代价:( 3 / 4 2 ) 0 c n 2 = c n 2 (3/4^2)^0\ cn^2 = cn^2 ( 3/ 4 2 ) 0 c n 2 = c n 2
第1层的代价:( 3 / 4 2 ) 1 c n 2 (3/4^2)^1\ cn^2 ( 3/ 4 2 ) 1 c n 2
第2层的代价:( 3 / 4 2 ) 2 c n 2 (3/4^2)^2\ cn^2 ( 3/ 4 2 ) 2 c n 2
第3层的代价:( 3 / 4 2 ) 3 c n 2 (3/4^2)^3\ cn^2 ( 3/ 4 2 ) 3 c n 2
第i层的代价: ( 3 / 4 2 ) i c n 2 (3/4^2)^i\ cn^2 ( 3/ 4 2 ) i c n 2
第h - 1层的代价: ( 3 / 4 2 ) log 4 n − 1 c n 2 (3/4^2)^{\log_4 n - 1} \ cn^2 ( 3/ 4 2 ) l o g 4 n − 1 c n 2
而最后一层代价根据换底公式:3 log 4 n × Θ ( 1 ) = n log 4 3 × Θ ( 1 ) = Θ ( n log 4 3 ) 3^{\log_4 n} \times \Theta(1) = n^{\log_4 3} \times \Theta(1) = \Theta(n^{\log_4 3}) 3 l o g 4 n × Θ ( 1 ) = n l o g 4 3 × Θ ( 1 ) = Θ ( n l o g 4 3 )
总代价为:
T ( n ) = c n 2 + ( 3 / 4 2 ) 1 c n 2 + ( 3 / 4 2 ) 2 c n 2 + ⋯ + ( 3 / 4 2 ) log 4 n − 1 c n 2 + Θ ( n log 4 3 ) = c n 2 × ( 1 + ( 3 / 4 2 ) 1 + ( 3 / 4 2 ) 2 + ⋯ + ( 3 / 4 2 ) log 4 n − 1 ) + Θ ( n log 4 3 ) = c n 2 × ( 3 / 4 2 ) log 4 n − 1 3 / 4 2 − 1 + Θ ( n log 4 3 ) \begin{align*}
T(n) &= cn^2 + (3/4^2)^1\ cn^2 + (3/4^2)^2\ cn^2 + \cdots + (3/4^2)^{\log_4 n - 1}\ cn^2 + \Theta(n^{\log_4 3}) \\
&= cn^2 \times (1 + (3/4^2)^1 + (3/4^2)^2 + \cdots + (3/4^2)^{\log_4 n - 1}) + \Theta(n^{\log_4 3}) \\
&= cn^2 \times \frac{(3/4^2)^{\log_4 n} - 1}{3/4^2 - 1} +\Theta(n^{\log_4 3})
\end{align*} T ( n ) = c n 2 + ( 3/ 4 2 ) 1 c n 2 + ( 3/ 4 2 ) 2 c n 2 + ⋯ + ( 3/ 4 2 ) l o g 4 n − 1 c n 2 + Θ ( n l o g 4 3 ) = c n 2 × ( 1 + ( 3/ 4 2 ) 1 + ( 3/ 4 2 ) 2 + ⋯ + ( 3/ 4 2 ) l o g 4 n − 1 ) + Θ ( n l o g 4 3 ) = c n 2 × 3/ 4 2 − 1 ( 3/ 4 2 ) l o g 4 n − 1 + Θ ( n l o g 4 3 ) 到这一步,我们已经成功使用参数去表示这个递归式。接下来的解需要使用微积分的知识,使用一个无穷范围以消除指数。
我们在实际情况中,可能还会遇到递归树节点参差不齐的情况,例如:
T ( n ) = T ( n / 3 ) + T ( 2 n / 3 ) + n T(n) = T(n/3) + T(2n/3) + n T ( n ) = T ( n /3 ) + T ( 2 n /3 ) + n
这种情况下的递归树子节点的代价不一样,因为其节点的规模一个为父节点的 1 / 3 1/3 1/3 2 / 3 2/3 2/3
我们可以分别计算最浅节点和最深节点的深度:
节点规模为 1 / 3 1/3 1/3 h 1 h_1 h 1 ( 1 3 ) h 1 n = 1 ⟹ h 1 = log 3 n (\frac{1}{3})^{h_1}\ n = 1 \implies h_1 = \log_3 n ( 3 1 ) h 1 n = 1 ⟹ h 1 = log 3 n
节点规模为 2 / 3 2/3 2/3 h 2 h_2 h 2 ( 2 3 ) h 2 n = 1 ⟹ h 2 = log 3 2 n (\frac{2}{3})^{h_2}\ n = 1 \implies h_2 = \log_{\frac{3}{2}} n ( 3 2 ) h 2 n = 1 ⟹ h 2 = log 2 3 n
因为 h 2 > h 1 h_2 > h_1 h 2 > h 1 2 / 3 2/3 2/3
在计算每层代价的时候,我们可以发现,它应该是一个分段的函数:
当深度 d ≤ h 1 d \le h_1 d ≤ h 1 c n cn c n
当深度 h 1 < d ≤ h 2 h_1 \lt d \le h_2 h 1 < d ≤ h 2 < c n < cn < c n
但是我们还是没法确定每层代价的表达式,只能估计一个模糊的边界。于是,我们假设两个在深度为 h 1 h_1 h 1 h 2 h_2 h 2
当一颗满二叉树的深度为 h 1 h_1 h 1 Θ ( 1 ) \Theta(1) Θ ( 1 )
它最后一层的节点数量为 2 h 1 = 2 log 3 n 2^{h_1} = 2^{\log_3 n} 2 h 1 = 2 l o g 3 n 2 log 3 n × Θ ( 1 ) = n log 3 2 × Θ ( 1 ) = Θ ( n log 3 2 ) 2^{\log_3 n} \times \Theta(1) = n^{\log_3 2} \times \Theta(1) = \Theta(n^{\log_3 2}) 2 l o g 3 n × Θ ( 1 ) = n l o g 3 2 × Θ ( 1 ) = Θ ( n l o g 3 2 )
于是该满二叉树的总代价为:
c n × ( log 3 n − 1 ) + Θ ( n log 3 2 ) = c n log 3 n + Θ ( n log 3 2 ) − c n = Ω ( n log n ) \begin{align*}
&cn \times (\log_3 n - 1) + \Theta(n^{\log_3 2}) \\
&= cn\log_3 n + \Theta(n^{\log_3 2}) - cn \\
&= \Omega(n\log n)
\end{align*} c n × ( log 3 n − 1 ) + Θ ( n l o g 3 2 ) = c n log 3 n + Θ ( n l o g 3 2 ) − c n = Ω ( n log n )
当一颗满二叉树的深度为 h 2 h_2 h 2 2 h 2 = 2 log 3 2 n 2^{h_2} = 2^{\log_{\frac{3}{2}} n} 2 h 2 = 2 l o g 2 3 n 2 log 3 2 n × Θ ( 1 ) = n log 3 2 2 × Θ ( 1 ) = Θ ( n log 3 2 2 ) 2^{\log_{\frac{3}{2}} n} \times \Theta(1) = n^{\log_{\frac{3}{2}}2} \times \Theta(1) = \Theta(n^{\log_{\frac{3}{2}}2}) 2 l o g 2 3 n × Θ ( 1 ) = n l o g 2 3 2 × Θ ( 1 ) = Θ ( n l o g 2 3 2 )
于是该满二叉树的总代价为:
c n × ( log 3 2 n − 1 ) + Θ ( n log 3 2 2 ) = c n log 3 2 n + Θ ( n log 3 2 2 ) − c n = O ( n log n ) \begin{align*}
&cn \times (\log_{\frac{3}{2}} n - 1) + \Theta(n^{\log_{\frac{3}{2}}2}) \\
&= cn\log_{\frac{3}{2}} n + \Theta(n^{\log_{\frac{3}{2}}2}) - cn \\
&= O(n\log n)
\end{align*}
c n × ( log 2 3 n − 1 ) + Θ ( n l o g 2 3 2 ) = c n log 2 3 n + Θ ( n l o g 2 3 2 ) − c n = O ( n log n )
所以综合起来,我们可以猜测递归式的解为:T ( n ) = Θ ( n log n ) T(n) = \Theta(n\log n) T ( n ) = Θ ( n log n )
因为是一个粗略的边界,我们需要使用代入进行验证。即证明:T ( n ) ≤ d n l g n T(n)\le dn\ lgn T ( n ) ≤ d n l g n d > 0 d>0 d > 0 c n cn c n Θ ( n ) \Theta(n) Θ ( n )
T ( n ) ≤ T ( n / 3 ) + T ( 2 n / 3 ) + Θ ( n ) ≤ d ( n / 3 ) lg ( n / 3 ) + d ( 2 n / 3 ) lg ( 2 n / 3 ) + c n = d ( n / 3 ) ( lg n − lg 3 ) + d ( 2 n / 3 ) ( lg n − lg ( 3 / 2 ) ) + c n = d n lg n − ( d ( n / 3 ) lg 3 + d ( 2 n / 3 ) lg ( 3 / 2 ) ) + c n = d n lg n − d [ ( 1 / 3 ) n lg 3 + ( 2 / 3 ) n lg 3 − ( 2 / 3 ) n lg 2 ] + c n = d n lg n − d ( lg 3 n − ( 2 / 3 ) n ) + c n ≤ d n lg n if − d ( lg 3 n − ( 2 / 3 ) n ) + c n ≤ 0 d ≥ c lg 3 − 2 / 3 \begin{align*}
T(n) &\le T(n/3) + T(2n/3) + \Theta(n) \\
&\le d(n/3) \lg(n/3) + d(2n/3) \lg(2n/3) + cn \\
&= d(n/3) (\lg n - \lg 3) + d(2n/3) (\lg n - \lg(3/2)) + cn \\
&= dn \lg n - (d(n/3)\lg 3 + d(2n/3) \lg(3/2)) + cn \\
&= dn \lg n - d[(1/3)n \lg 3 + (2/3)n \lg 3 - (2/3)n \lg 2] + cn \\
&= dn \lg n - d(\lg 3 n- (2/3)n) + cn \\
&\le dn \lg n \\\\
\text{ if } &- d(\lg 3 n- (2/3)n) + cn \le 0 \\
&d \ge \frac{c}{\lg 3 - 2/3}
\end{align*} T ( n ) if ≤ T ( n /3 ) + T ( 2 n /3 ) + Θ ( n ) ≤ d ( n /3 ) lg ( n /3 ) + d ( 2 n /3 ) lg ( 2 n /3 ) + c n = d ( n /3 ) ( lg n − lg 3 ) + d ( 2 n /3 ) ( lg n − lg ( 3/2 )) + c n = d n lg n − ( d ( n /3 ) lg 3 + d ( 2 n /3 ) lg ( 3/2 )) + c n = d n lg n − d [( 1/3 ) n lg 3 + ( 2/3 ) n lg 3 − ( 2/3 ) n lg 2 ] + c n = d n lg n − d ( lg 3 n − ( 2/3 ) n ) + c n ≤ d n lg n − d ( lg 3 n − ( 2/3 ) n ) + c n ≤ 0 d ≥ lg 3 − 2/3 c 同理,可以验证其下界,最后得到递归式解为:T ( n ) = Θ ( n log n ) T(n) = \Theta(n\log n) T ( n ) = Θ ( n log n )
主方法 / Master method# 主方法主要来自于递归树法的总结,适用于求解下面格式的递归式:T ( n ) = a T ( n / b ) + f ( n ) T(n) = aT(n/b) + f(n) T ( n ) = a T ( n / b ) + f ( n ) a > 0 , b > 1 a>0,\ b>1 a > 0 , b > 1
f ( n ) f(n) f ( n ) 驱动函数 (driving function),它是一个渐进非负函数。它是基础情况下的代价。
这个通式我们可以得到以下信息:
子问题数量: a a a
子问题规模: 1 / b 1/b 1/ b
递归树的深度: n b h = 1 ⟹ h = log b n \frac{n}{b^h} = 1 \implies h = \log_b n b h n = 1 ⟹ h = log b n
递归树深度第i层的结点个数: a i a^i a i
递归树最后一层的结点个数: a h = a log b n = n log b a a^h = a^{\log_b n} = n^{\log_b a} a h = a l o g b n = n l o g b a
若最后一层结点都是 Θ ( 1 ) \Theta(1) Θ ( 1 )
C h = a h × Θ ( 1 ) = n log b a × Θ ( 1 ) = Θ ( n log b a ) C_h = a^h \times \Theta(1) = n^{\log_b a} \times \Theta(1) = \Theta(n^{\log_b a}) C h = a h × Θ ( 1 ) = n l o g b a × Θ ( 1 ) = Θ ( n l o g b a ) 而其他层结点的代价为:
C other = f ( n ) + a f ( n / b ) + a f ( n / b 2 ) + ⋯ + a f ( n / b h − 1 ) = f ( n ) + a ( f ( n / b ) + f ( n / b 2 ) + ⋯ + f ( n / b h − 1 ) ) = ∑ i = 0 log b n − 1 a i f ( n / b i ) \begin{align*}
C_{\text{other}} = &f(n) + af(n/b) + af(n/b^2) + \cdots + af(n/b^{h-1}) \\
&= f(n) + a(f(n/b) + f(n/b^2) + \cdots + f(n/b^{h-1})) \\
&=\sum \limits_{i=0}^{\log_b n-1} a^i f(n/b^i)
\end{align*} C other = f ( n ) + a f ( n / b ) + a f ( n / b 2 ) + ⋯ + a f ( n / b h − 1 ) = f ( n ) + a ( f ( n / b ) + f ( n / b 2 ) + ⋯ + f ( n / b h − 1 )) = i = 0 ∑ l o g b n − 1 a i f ( n / b i ) 那么最终的代价可以表示为:
C = C h + C other = Θ ( n log b a ) + ∑ i = 0 log b n − 1 a i f ( n / b i ) \begin{align*}
C &= C_h + C_{\text{other}} \\
&= \Theta(n^{\log_b a}) + \sum \limits_{i=0}^{\log_b n-1} a^i f(n/b^i)
\end{align*} C = C h + C other = Θ ( n l o g b a ) + i = 0 ∑ l o g b n − 1 a i f ( n / b i ) 对于这样的递归式,它的边界由 C h C_h C h C other C_{\text{other}} C other n n n 指数大 的那个决定。于是我们可以进行分类讨论,即主方法的定义:
Definition Case 1: (f ( n ) < n log b a f(n) < n^{\log_b a} f ( n ) < n l o g b a ϵ > 0 \epsilon > 0 ϵ > 0 f ( n ) = O ( n log b a − ϵ ) f(n) = O(n^{\log_b a-\epsilon}) f ( n ) = O ( n l o g b a − ϵ ) T ( n ) = Θ ( n log b a ) T(n) = Θ(n^{\log_b a}) T ( n ) = Θ ( n l o g b a ) 叶子节点 。
Case 2: (f ( n ) ≈ n log b a f(n) \approx n^{\log_b a} f ( n ) ≈ n l o g b a k ≥ 0 k \ge 0 k ≥ 0 f ( n ) = Θ ( n log b a lg k n ) f(n) = \Theta(n^{\log_b a }\lg^k n) f ( n ) = Θ ( n l o g b a lg k n ) T ( n ) = Θ ( n log b a lg k + 1 n ) T(n) = \Theta(n^{\log_b a }\lg^{k+1} n) T ( n ) = Θ ( n l o g b a lg k + 1 n ) Θ ( n log b a lg k n ) \Theta(n^{\log_b a} \lg^k n) Θ ( n l o g b a lg k n ) Θ ( lg n ) \Theta(\lg n) Θ ( lg n )
Case 3: (f ( n ) > n log b a f(n) > n^{\log_b a} f ( n ) > n l o g b a ϵ > 0 \epsilon > 0 ϵ > 0 f ( n ) = Ω ( n log b a + ϵ ) f(n) = \Omega(n^{\log_b a+\epsilon}) f ( n ) = Ω ( n l o g b a + ϵ ) f ( n ) f(n) f ( n ) n n n a f ( n / b ) ≤ c f ( n ) , c < 1 af(n/b) ≤ cf(n), c \lt 1 a f ( n / b ) ≤ c f ( n ) , c < 1 T ( n ) = Θ ( f ( n ) ) T(n) = \Theta(f(n)) T ( n ) = Θ ( f ( n )) 根节点 。
下面三个例题分别是对应了三种不同情况下的主方法的应用:
T ( n ) = 2 T ( n / 4 ) + 1 T(n) = 2T(n/4) + 1 T ( n ) = 2 T ( n /4 ) + 1
分析可知:f ( n ) = 1 f(n) = 1 f ( n ) = 1 n log b a = n log 4 2 = n 1 / 2 n^{\log_b a} = n^{\log_4 2} = n^{1/2} n l o g b a = n l o g 4 2 = n 1/2 f ( n ) < n log b a f(n) < n^{\log_b a} f ( n ) < n l o g b a T ( n ) = Θ ( n 1 / 2 ) T(n) = Θ(n^{1/2}) T ( n ) = Θ ( n 1/2 )
T ( n ) = 2 T ( n / 4 ) + n lg 2 n T(n) = 2T(n/4) + \sqrt{n}\lg^2 n T ( n ) = 2 T ( n /4 ) + n lg 2 n
分析可知:f ( n ) = n lg 2 n f(n) = \sqrt{n}\lg^2 n f ( n ) = n lg 2 n n log b a = n log 4 2 = n 1 / 2 n^{\log_b a} = n^{\log_4 2} = n^{1/2} n l o g b a = n l o g 4 2 = n 1/2 f ( n ) = Θ ( n 1 / 2 lg 2 n ) = Θ ( n log b a lg 2 n ) f(n) = Θ(n^{1/2} \lg^2 n) = Θ(n^{\log_b a} \lg^2 n) f ( n ) = Θ ( n 1/2 lg 2 n ) = Θ ( n l o g b a lg 2 n ) T ( n ) = Θ ( n 1 / 2 lg 3 n ) T(n) = Θ(n^{1/2} \lg^3 n) T ( n ) = Θ ( n 1/2 lg 3 n )
T ( n ) = 2 T ( n / 4 ) + n 2 T(n) = 2T(n/4) + n^2 T ( n ) = 2 T ( n /4 ) + n 2
分析可知:f ( n ) = n 2 f(n) = n^2 f ( n ) = n 2 n log b a = n log 4 2 = n 1 / 2 n^{\log_b a} = n^{\log_4 2} = n^{1/2} n l o g b a = n l o g 4 2 = n 1/2 f ( n ) > n log b a f(n) > n^{\log_b a} f ( n ) > n l o g b a 2 f ( n / 4 ) = ( 1 / 8 ) n 2 ≤ c f ( n ) 2f(n/4) = (1/8)n^2 ≤ cf(n) 2 f ( n /4 ) = ( 1/8 ) n 2 ≤ c f ( n ) 0 < c < 1 0<c<1 0 < c < 1 T ( n ) = Θ ( n 2 ) T(n) = Θ(n^2) T ( n ) = Θ ( n 2 )
但是主方法并不能覆盖所有的递归式,它会出现空隙无法使用。
当 f ( n ) f(n) f ( n ) n log b a n^{\log_b a} n l o g b a
当 f ( n ) = o ( n log b a ) f(n) = o(n^{\log_b a}) f ( n ) = o ( n l o g b a ) n log b a n^{\log_b a} n l o g b a f ( n ) f(n) f ( n )
当 f ( n ) = ω ( n log b a ) f(n) = ω(n^{\log_b a}) f ( n ) = ω ( n l o g b a ) n log b a n^{\log_b a} n l o g b a f ( n ) f(n) f ( n )
解决这类递归式可以尝试使用其他方法,或Akra-Bazzi 递归式,这里不在正文处涉及。
Exercises in Divide-and-Conquer# 下面我们通过一些练习,去加深对解递归式的三种方法的理解。
证明:T ( n ) = T ( n − 2 ) + n 2 T(n) = T(n - 2) + n^2 T ( n ) = T ( n − 2 ) + n 2 T ( n ) = Θ ( n 3 ) T(n) = \Theta(n^3) T ( n ) = Θ ( n 3 )
因为题目要求我们证明的是 Θ \Theta Θ
我们可以设存在常数 c > 0 c > 0 c > 0 n 0 n_0 n 0 n ≥ n 0 n \ge n_0 n ≥ n 0 T ( n ) ≤ c n 3 T(n) \le cn^3 T ( n ) ≤ c n 3
假设对于所有的 k < n k < n k < n T ( k ) ≤ c k 3 T(k) \le ck^3 T ( k ) ≤ c k 3 T ( n − 2 ) ≤ c ( n − 2 ) 3 T(n - 2) \le c(n - 2)^3 T ( n − 2 ) ≤ c ( n − 2 ) 3
代入原递归式得到:
T ( n ) ≤ c ( n − 2 ) 3 + n 2 = c ( n 3 − 6 n 2 + 12 n − 8 ) + n 2 = c n 3 − 6 c n 2 + 12 c n − 8 c + n 2 ≤ c n 3 if − 6 c n 2 + 12 c n − 8 c + n 2 ≤ 0 ( 1 − 6 c ) n 2 + 12 c n − 8 c ≤ 0 \begin{align*}
T(n) &\le c(n - 2)^3 + n^2 \\
&= c(n^3-6n^2+12n-8)+n^2 \\
&= cn^3 - 6cn^2 + 12cn - 8c + n^2 \\
&\le cn^3 & \text{ if } - 6cn^2 + 12cn - 8c + n^2 \le 0 \\
& & (1-6c)n^2 +12cn -8c \le 0
\end{align*} T ( n ) ≤ c ( n − 2 ) 3 + n 2 = c ( n 3 − 6 n 2 + 12 n − 8 ) + n 2 = c n 3 − 6 c n 2 + 12 c n − 8 c + n 2 ≤ c n 3 if − 6 c n 2 + 12 c n − 8 c + n 2 ≤ 0 ( 1 − 6 c ) n 2 + 12 c n − 8 c ≤ 0 为了使这个不等式在 n ≥ n 0 n \ge n_0 n ≥ n 0 n 0 n_0 n 0 1 − 6 c < 0 ⟹ c > 1 6 1- 6c \lt 0 \implies c > \frac{1}{6} 1 − 6 c < 0 ⟹ c > 6 1
因此在 c > 1 6 c > \frac{1}{6} c > 6 1 T ( n ) = O ( n 3 ) T(n) = O(n^3) T ( n ) = O ( n 3 )
设存在常数 d > 0 d > 0 d > 0 n 0 n_0 n 0 n ≥ n 0 n \ge n_0 n ≥ n 0 T ( n ) ≥ d n 3 T(n) \ge dn^3 T ( n ) ≥ d n 3
假设对于所有的 k < n k < n k < n T ( k ) ≥ d k 3 T(k) \ge dk^3 T ( k ) ≥ d k 3 T ( n − 2 ) ≥ d ( n − 2 ) 3 T(n - 2) \ge d(n - 2)^3 T ( n − 2 ) ≥ d ( n − 2 ) 3
代入原递归式得到:
T ( n ) ≥ d ( n − 2 ) 3 + n 2 = d ( n 3 − 6 n 2 + 12 n − 8 ) + n 2 = d n 3 − 6 d n 2 + 12 d n − 8 d + n 2 ≥ d n 3 if − 6 d n 2 + 12 d n − 8 d + n 2 ≥ 0 ( 1 − 6 d ) n 2 + 12 d n − 8 d ≥ 0 \begin{align*}
T(n) &\ge d(n - 2)^3 + n^2 \\
&= d(n^3-6n^2+12n-8)+n^2 \\
&= dn^3 - 6dn^2 + 12dn - 8d + n^2 \\
&\ge dn^3 & \text{ if } - 6dn^2 + 12dn - 8d + n^2 \ge 0 \\
& & (1-6d)n^2 +12dn -8d \ge 0
\end{align*} T ( n ) ≥ d ( n − 2 ) 3 + n 2 = d ( n 3 − 6 n 2 + 12 n − 8 ) + n 2 = d n 3 − 6 d n 2 + 12 d n − 8 d + n 2 ≥ d n 3 if − 6 d n 2 + 12 d n − 8 d + n 2 ≥ 0 ( 1 − 6 d ) n 2 + 12 d n − 8 d ≥ 0 为了使这个不等式在 n ≥ n 0 n \ge n_0 n ≥ n 0 n 0 n_0 n 0 1 − 6 d ≥ 0 ⟹ 0 < d ≤ 1 6 1- 6d \ge 0 \implies 0 \lt d \le \frac{1}{6} 1 − 6 d ≥ 0 ⟹ 0 < d ≤ 6 1
所以当满足 0 < d ≤ 1 6 0 \lt d \le \frac{1}{6} 0 < d ≤ 6 1 T ( n ) = Θ ( n 3 ) T(n) = \Theta(n^3) T ( n ) = Θ ( n 3 )
综上,T ( n ) = Θ ( n 3 ) T(n) = \Theta(n^3) T ( n ) = Θ ( n 3 )
对于递归式 T ( n ) = 4 T ( n / 3 ) + n T(n) = 4T(n/3) + n T ( n ) = 4 T ( n /3 ) + n
将该递归式转化为递归树,如下图:
我们可以通过这个图计算出:
递归树的深度为: n / 3 d = 1 ⟹ d = log 3 n n/3^d = 1 \implies d = \log_3 n n / 3 d = 1 ⟹ d = log 3 n
递归树中第i层的结点数:4 i 4^i 4 i
最后一层的代价为:4 d × Θ ( 1 ) = Θ ( n log 3 4 ) 4^d \times \Theta(1) = \Theta(n^{\log_3 4}) 4 d × Θ ( 1 ) = Θ ( n l o g 3 4 )
观察到代价是一个等比数列,所以我们整理可以得到总代价:
C o s t = [ n + ( 4 3 ) n + ( 4 3 ) 2 n + ⋯ + ( 4 3 ) d − 1 n ] + Θ ( n log 3 4 ) = 3 n × ( 4 d 3 d − 1 ) + Θ ( n log 3 4 ) = 3 n × ( 4 log 3 n 3 log 3 n − 1 ) + Θ ( n log 3 4 ) = 3 n × ( n log 3 4 n log 3 3 − 1 ) + Θ ( n log 3 4 ) = 3 n log 3 4 − 3 n + Θ ( n log 3 4 ) \begin{align*}
Cost&=[n+(\frac{4}{3}) n+(\frac{4}{3})^2 n+ \dots + (\frac{4}{3})^{d-1} n]+\Theta(n^{\log_3 4}) \\
&=3n \times (\frac{4^d}{3^d}-1) + \Theta(n^{\log_3 4}) \\
&=3n \times (\frac{4^{\log_3 n}}{3^{\log_3 n}}-1) + \Theta(n^{\log_3 4}) \\
&=3n \times (\frac{n^{\log_3 4}}{n^{\log_3 3}}-1) + \Theta(n^{\log_3 4}) \\
&=3n^{\log_3 4} - 3n + \Theta(n^{\log_3 4})
\end{align*} C os t = [ n + ( 3 4 ) n + ( 3 4 ) 2 n + ⋯ + ( 3 4 ) d − 1 n ] + Θ ( n l o g 3 4 ) = 3 n × ( 3 d 4 d − 1 ) + Θ ( n l o g 3 4 ) = 3 n × ( 3 l o g 3 n 4 l o g 3 n − 1 ) + Θ ( n l o g 3 4 ) = 3 n × ( n l o g 3 3 n l o g 3 4 − 1 ) + Θ ( n l o g 3 4 ) = 3 n l o g 3 4 − 3 n + Θ ( n l o g 3 4 ) 因为 log 3 4 > 1 ⟹ n log 3 4 > n \log_3 4 > 1 \implies n^{\log_3 4} > n log 3 4 > 1 ⟹ n l o g 3 4 > n T ( n ) = Θ ( n log 3 4 ) T(n) = \Theta(n^{\log_3 4}) T ( n ) = Θ ( n l o g 3 4 )
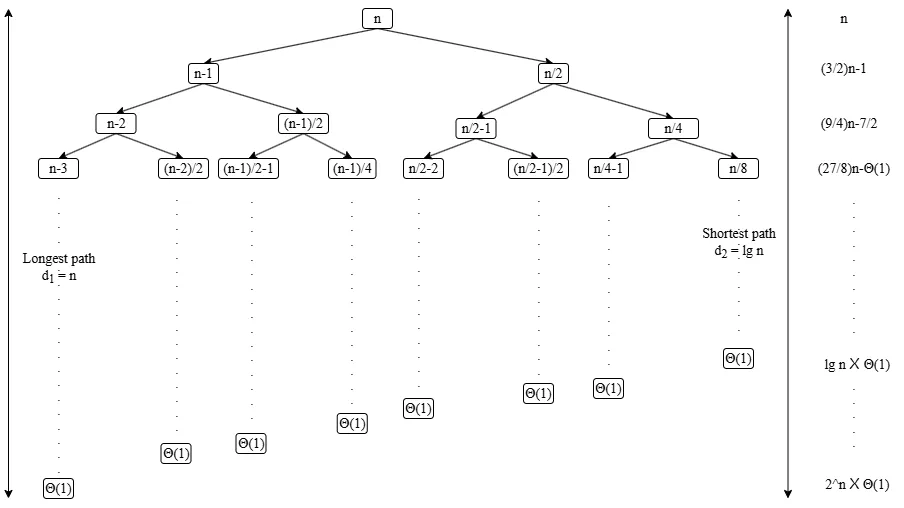
对于递归式 T ( n ) = T ( n − 1 ) + T ( n / 2 ) + n T(n) = T(n - 1) + T(n / 2) + n T ( n ) = T ( n − 1 ) + T ( n /2 ) + n
将该递归式转化为递归树,如下图:
这个递归图比较奇怪,左侧减的没有右侧加的到底快,我们只能估计它的边界。
本题需要我们求它的上界,即取最长的路径作为树的深度进行计算。可以得到:
递归树的深度 (最深的路径边数) 为: d 1 = n − 1 d_1 = n - 1 d 1 = n − 1
递归树中d_1层的结点数:2 d 1 2^{d_1} 2 d 1
观察到代价中n的系数是一个等比数列,后面跟着的是一个常数。我们可以忽略这个常数,得到总代价:
C o s t ≤ [ n + ( 3 / 2 ) n − 1 + ( 3 / 2 ) 2 n − 7 / 2 + ( 3 / 2 ) 3 − Θ ( 1 ) ⋯ + ( 3 / 2 ) d 1 n − Θ ( 1 ) ] ≤ 2 n × ( ( 3 / 2 ) n − 1 ) − Θ ( 1 ) \begin{align*}
Cost&\le[n+(3/2)n-1+(3/2)^2n-7/2+(3/2)^3 - \Theta(1) \dots + (3/2)^{d_1}n - \Theta(1)]\\
&\le 2n \times ((3/2)^n - 1) - \Theta(1)\\
\end{align*} C os t ≤ [ n + ( 3/2 ) n − 1 + ( 3/2 ) 2 n − 7/2 + ( 3/2 ) 3 − Θ ( 1 ) ⋯ + ( 3/2 ) d 1 n − Θ ( 1 )] ≤ 2 n × (( 3/2 ) n − 1 ) − Θ ( 1 ) 观察到代价由 2 n × ( 3 / 2 ) n 2n \times (3/2)^n 2 n × ( 3/2 ) n Θ ( 2 n ) \Theta(2^n) Θ ( 2 n ) ( 3 / 2 ) < 2 (3/2) < 2 ( 3/2 ) < 2 n n n Θ ( 2 n ) > 2 n × ( 3 / 2 ) n \Theta(2^n) > 2n \times (3/2)^n Θ ( 2 n ) > 2 n × ( 3/2 ) n T ( n ) = O ( 2 n ) T(n) = O(2^n) T ( n ) = O ( 2 n )
对于递归式 T ( n ) = 2 T ( n / 4 ) + n T(n) = 2T(n/4) + \sqrt n T ( n ) = 2 T ( n /4 ) + n
我们对比分水岭函数 n log b a n^{\log_b a} n l o g b a f ( n ) f(n) f ( n )
n log b a = n log 4 2 = n 1 2 n^{\log_b a} = n^{\log_4 2} = n^{\frac{1}{2}} n l o g b a = n l o g 4 2 = n 2 1 f ( n ) = n = n 1 2 f(n) = \sqrt n = n ^ {\frac{1}{2}} f ( n ) = n = n 2 1 可以发现 n log b a = f ( n ) n^{\log_b a} = f(n) n l o g b a = f ( n ) k = 0 k = 0 k = 0 f ( n ) = Θ ( n log b a lg k n ) = n 1 2 f(n) = \Theta(n^{\log_b a} \lg^k n) = n^{\frac{1}{2}} f ( n ) = Θ ( n l o g b a lg k n ) = n 2 1
可以应用主方法的Case 2,得到 T ( n ) = Θ ( n log b a lg n ) = Θ ( n lg n ) T(n) = \Theta(n^{\log_b a} \lg n) = \Theta(\sqrt n \lg n) T ( n ) = Θ ( n l o g b a lg n ) = Θ ( n lg n )
Master Method - Case 2 Case 2: (f ( n ) ≈ n log b a f(n) \approx n^{\log_b a} f ( n ) ≈ n l o g b a k ≥ 0 k \ge 0 k ≥ 0 f ( n ) = Θ ( n log b a lg k n ) f(n) = \Theta(n^{\log_b a }\lg^k n) f ( n ) = Θ ( n l o g b a lg k n ) T ( n ) = Θ ( n log b a lg k + 1 n ) T(n) = \Theta(n^{\log_b a }\lg^{k+1} n) T ( n ) = Θ ( n l o g b a lg k + 1 n ) Θ ( n log b a lg k n ) \Theta(n^{\log_b a} \lg^k n) Θ ( n l o g b a lg k n ) Θ ( lg n ) \Theta(\lg n) Θ ( lg n )
对于递归式 T ( n ) = 4 T ( n / 2 ) + n 2 lg n T(n) = 4T(n/2) + n^2\lg n T ( n ) = 4 T ( n /2 ) + n 2 lg n
我们对比分水岭函数 n log b a n^{\log_b a} n l o g b a f ( n ) f(n) f ( n )
n log b a = n log 2 4 = n 2 n^{\log_b a} = n^{\log_2 4} = n^2 n l o g b a = n l o g 2 4 = n 2 f ( n ) = n 2 lg n f(n) = n^2\lg n f ( n ) = n 2 lg n 可以发现两个函数之间相差了一个 lg n \lg n lg n k = 1 k = 1 k = 1 f ( n ) = Θ ( n log b a lg k n ) = n 2 lg n f(n) = \Theta(n^{\log_b a}\lg^k n) = n^2\lg n f ( n ) = Θ ( n l o g b a lg k n ) = n 2 lg n
所以 T ( n ) = Θ ( n 2 lg 2 n ) T(n) = \Theta(n^2\lg^2 n) T ( n ) = Θ ( n 2 lg 2 n )
对于递归式 T ( n ) = 2 T ( n / 4 ) + n T(n) = 2T(n/4) + n T ( n ) = 2 T ( n /4 ) + n
我们对比分水岭函数 n log b a n^{\log_b a} n l o g b a f ( n ) f(n) f ( n )
n log b a = n log 4 2 = n 1 2 n^{\log_b a} = n^{\log_4 2} = n^{\frac{1}{2}} n l o g b a = n l o g 4 2 = n 2 1 f ( n ) = n f(n) = n f ( n ) = n 因为 n log b a < f ( n ) n^{\log_b a} \lt f(n) n l o g b a < f ( n )
进一步检测: 2 × n 4 = n 2 ≤ c n 2\times \frac{n}{4} = \frac{n}{2} \le cn 2 × 4 n = 2 n ≤ c n c , c ∈ [ 1 2 , 1 ] c,\ c\in [\frac{1}{2},1] c , c ∈ [ 2 1 , 1 ]
所以 T ( n ) = Θ ( f ( n ) ) = Θ ( n ) T(n) = \Theta(f(n)) = \Theta(n) T ( n ) = Θ ( f ( n )) = Θ ( n )
Master Method - Case 3 Case 3: (f ( n ) > n log b a f(n) > n^{\log_b a} f ( n ) > n l o g b a ϵ > 0 \epsilon > 0 ϵ > 0 f ( n ) = Ω ( n log b a + ϵ ) f(n) = \Omega(n^{\log_b a+\epsilon}) f ( n ) = Ω ( n l o g b a + ϵ ) f ( n ) f(n) f ( n ) n n n a f ( n / b ) ≤ c f ( n ) , c < 1 af(n/b) ≤ cf(n), c \lt 1 a f ( n / b ) ≤ c f ( n ) , c < 1 T ( n ) = Θ ( f ( n ) ) T(n) = \Theta(f(n)) T ( n ) = Θ ( f ( n )) 根节点 。
对于递归式 T ( n ) = 7 T ( n / 2 ) + n T(n) = 7T(n/2) + n T ( n ) = 7 T ( n /2 ) + n
我们对比分水岭函数 n log b a n^{\log_b a} n l o g b a f ( n ) f(n) f ( n )
n log b a = n lg 7 n^{\log_b a} = n^{\lg 7} n l o g b a = n l g 7 f ( n ) = n f(n) = n f ( n ) = n 明显:n log b a > f ( n ) n^{\log_b a} \gt f(n) n l o g b a > f ( n )
存在一个常数 ϵ = 6 > 0 \epsilon = 6 > 0 ϵ = 6 > 0 f ( n ) = O ( n log b a − ϵ ) = O ( n lg 7 − 6 ) f(n) = O(n^{\log_b a-\epsilon}) = O(n^{\lg 7-6}) f ( n ) = O ( n l o g b a − ϵ ) = O ( n l g 7 − 6 )
所以 T ( n ) = Θ ( n log b a ) = Θ ( n lg 7 ) T(n) = \Theta(n^{\log_b a}) = \Theta(n^{\lg 7}) T ( n ) = Θ ( n l o g b a ) = Θ ( n l g 7 )
Master Method - Case 1 Case 1: (f ( n ) < n log b a f(n) < n^{\log_b a} f ( n ) < n l o g b a ϵ > 0 \epsilon > 0 ϵ > 0 f ( n ) = O ( n log b a − ϵ ) f(n) = O(n^{\log_b a-\epsilon}) f ( n ) = O ( n l o g b a − ϵ ) T ( n ) = Θ ( n log b a ) T(n) = Θ(n^{\log_b a}) T ( n ) = Θ ( n l o g b a ) 叶子节点 。
Summary# 总结一下本节内容:本节主要介绍了三种解递归式的方法 - 代入法、递归树法和主方法。
好的,以下是《算法导论》(第4版)第4章中三种求解递归式方法的总结:
代入法 (Substitution Method): 本质上是一种 数学归纳法 。可以用来证明任何递归式的解,最大的难点在于需要 提前猜测 出解的正确形式。 解法步骤:
猜测 (Guess): 凭借经验或使用递归树法,猜测解的渐近形式,例如 T ( n ) = O ( g ( n ) ) T(n) = O(g(n)) T ( n ) = O ( g ( n )) 归纳假设 (Assume): 假设猜测对于所有小于 n n n k k k T ( k ) ≤ c ⋅ g ( k ) T(k) \le c \cdot g(k) T ( k ) ≤ c ⋅ g ( k ) O O O 证明 (Prove): 将归纳假设代入原递归式,通过数学推导证明 T ( n ) ≤ c ⋅ g ( n ) T(n) \le c \cdot g(n) T ( n ) ≤ c ⋅ g ( n ) 求解常数与边界: 在推导过程中,需要找到一个合适的常数 c > 0 c > 0 c > 0 n 0 n_0 n 0 n ≥ n 0 n \ge n_0 n ≥ n 0 配平: 有时为了使归纳成立,你需要从猜测中减去一个低阶项,例如猜测 T ( n ) ≤ c n 2 − d n T(n) \le c n^2 - d n T ( n ) ≤ c n 2 − d n T ( n ) ≤ c n 2 T(n) \le c n^2 T ( n ) ≤ c n 2
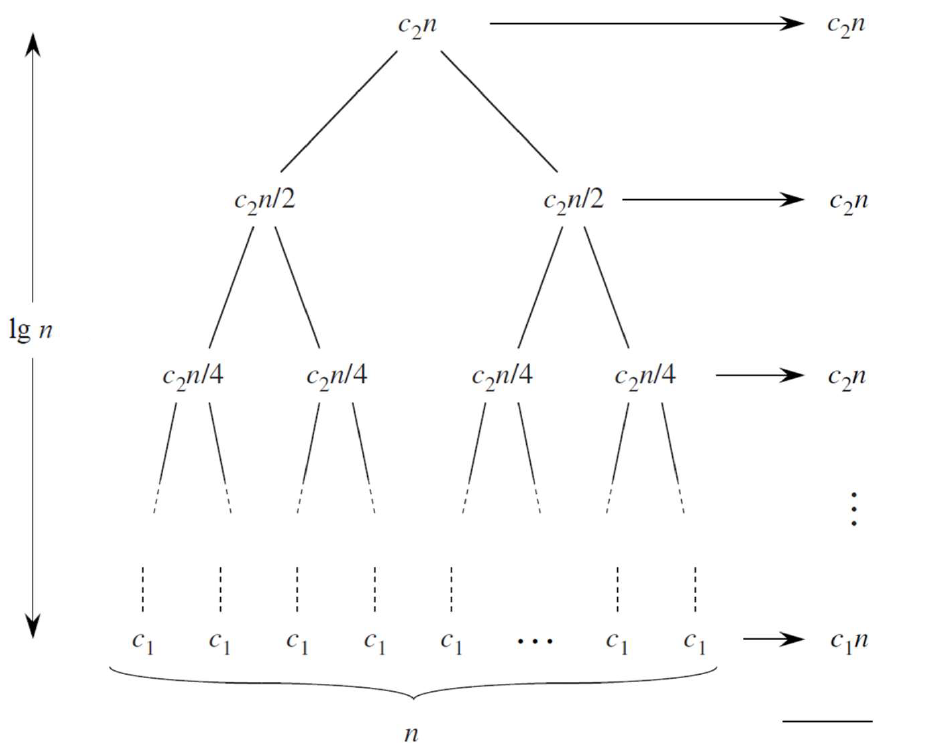
递归树法 (Recursion-Tree Method): 它非常直观,将递归式的代价在树的各个层级上进行可视化展开。适用于分析分治算法的递归式,特别是 T ( n ) = a T ( n / b ) + f ( n ) T(n) = aT(n/b) + f(n) T ( n ) = a T ( n / b ) + f ( n ) 解法步骤:
构建树: 画出递归树。根节点代表 f ( n ) f(n) f ( n ) a a a n / b n/b n / b f ( n / b ) f(n/b) f ( n / b ) 计算层代价: 计算树的第 i i i a i ⋅ f ( n / b i ) a^i \cdot f(n/b^i) a i ⋅ f ( n / b i ) 计算树深度 (高度): 确定树的深度 h h h log b n \log_b n log b n 计算叶子代价: 确定叶子节点的总数(通常是 a h = n log b a a^h = n^{\log_b a} a h = n l o g b a Θ ( n log b a ) \Theta(n^{\log_b a}) Θ ( n l o g b a ) 求和: 将所有层(从根到叶子之前的所有内部节点)的代价与叶子层的总代价相加。分析总和: 分析这个总和的渐近界,从而得出 T ( n ) T(n) T ( n )
主方法 (Master Method): 本质上是递归树法中三种常见情况(代价由叶子主导、由根主导、或均匀分布)的数学归纳总结。仅 适用于 T ( n ) = a T ( n / b ) + f ( n ) T(n) = aT(n/b) + f(n) T ( n ) = a T ( n / b ) + f ( n ) a ≥ 1 , b > 1 a \ge 1, b > 1 a ≥ 1 , b > 1 f ( n ) f(n) f ( n ) 解法步骤:
确定参数: 找出 a a a b b b f ( n ) f(n) f ( n ) 计算关键函数: 计算 g ( n ) = n log b a g(n) = n^{\log_b a} g ( n ) = n l o g b a 比较 f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n )
Case 1 (叶子主导): 如果 f ( n ) = O ( n log b a − ϵ ) f(n) = O(n^{\log_b a - \epsilon}) f ( n ) = O ( n l o g b a − ϵ ) ϵ > 0 \epsilon > 0 ϵ > 0 g ( n ) g(n) g ( n ) f ( n ) f(n) f ( n ) T ( n ) = Θ ( n log b a ) T(n) = \Theta(n^{\log_b a}) T ( n ) = Θ ( n l o g b a ) Case 2 (代价均衡): 如果 f ( n ) = Θ ( n log b a ⋅ log k n ) f(n) = \Theta(n^{\log_b a} \cdot \log^k n) f ( n ) = Θ ( n l o g b a ⋅ log k n ) k ≥ 0 k \ge 0 k ≥ 0 f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) log \log log T ( n ) = Θ ( n log b a ⋅ log k + 1 n ) T(n) = \Theta(n^{\log_b a} \cdot \log^{k+1} n) T ( n ) = Θ ( n l o g b a ⋅ log k + 1 n )
(最常见的子情况 k = 0 k=0 k = 0 f ( n ) = Θ ( n log b a ) f(n) = \Theta(n^{\log_b a}) f ( n ) = Θ ( n l o g b a ) T ( n ) = Θ ( n log b a log n ) T(n) = \Theta(n^{\log_b a} \log n) T ( n ) = Θ ( n l o g b a log n )
Case 3 (根代价主导): 如果 f ( n ) = Ω ( n log b a + ϵ ) f(n) = \Omega(n^{\log_b a + \epsilon}) f ( n ) = Ω ( n l o g b a + ϵ ) ϵ > 0 \epsilon > 0 ϵ > 0 f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) 并且 满足 正则条件 (regularity condition)(即 a f ( n / b ) ≤ c f ( n ) a f(n/b) \le c f(n) a f ( n / b ) ≤ c f ( n ) c < 1 c < 1 c < 1 n n n T ( n ) = Θ ( f ( n ) ) T(n) = \Theta(f(n)) T ( n ) = Θ ( f ( n ))
注意: 如果 f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) f ( n ) f(n) f ( n ) g ( n ) g(n) g ( n ) 经典排序算法# 在已经学习了分治算法中递归式的三种解法,但只是在理论上讨论,本节将回顾几种常见的排序算法 - 插入排序、归并排序、快速排序和快速选择排序,并适当应用之前所学的递归式解法,给出其性能分析。
插入排序 / Insertion sort# 插入排序是最基础的排序算法,其时间复杂度为 O ( n 2 ) O(n^2) O ( n 2 )
while j > 0 and A[j] > key
很明显的能看到,插入排序有两个循环体,一个用于比较,一个用于交换。在最坏的情况下,T ( n ) = O ( n 2 ) T(n) = O(n^2) T ( n ) = O ( n 2 )
最好情况则是当待排序序列为正序状态,则遍历完整个序列,当插入元素时,只比较一次就够了,所以此时复杂度为 O ( n ) O(n) O ( n )
基础的插入排序没有使用递归算法,我们可以用递归的方法代替循环体:为了排序 A[1,n],我们递归地排序A[1,n-1],然后把A[n]插入已排序的数组A[1,n-1]。
每一次递归中,我们都需要插入元素到有序数组中,这个过程需要一个循环。我们用递归代替外层循环,递归每次规模为 n − 1 n-1 n − 1
我们可以用这样的递归式表示它的运行时间:
T ( n ) = { Θ ( 1 ) i f n = 1 T ( n − 1 ) + Θ ( n ) i f n > 1 \begin{equation}
T(n) = \begin{cases}
\Theta(1) & if \ n=1 \\
T(n-1) + \Theta(n) & if\ n>1
\end{cases}
\end{equation} T ( n ) = { Θ ( 1 ) T ( n − 1 ) + Θ ( n ) i f n = 1 i f n > 1 我们分析它非常简单,对它画递归树,是一条直线:
c n . c ( n − 1 ) . c ( n − 2 ) . … . c ( n − n + 1 ) . Θ ( 1 ) \begin{align*}
cn \\
. \\
c(n-1) \\
. \\
c(n-2) \\
. \\
\dots \\
. \\
c(n-n+1) \\
. \\
\Theta(1)
\end{align*} c n . c ( n − 1 ) . c ( n − 2 ) . … . c ( n − n + 1 ) . Θ ( 1 ) 除了最后一层外是一个等差数列,有 n − 1 n-1 n − 1 T ( n ) = ( n − 1 ) ( c n + c ( n − n + 1 ) ) / 2 + Θ ( 1 ) = Θ ( n 2 ) T(n) = (n-1)(cn+c(n-n+1)) / 2 + \Theta(1) = \Theta(n^2) T ( n ) = ( n − 1 ) ( c n + c ( n − n + 1 )) /2 + Θ ( 1 ) = Θ ( n 2 )
插入排序的优化# 在子数组已经排序的情况下,我们可以用 二分查找(binary search)找到要插入的区间 ,使得插入排序的效率提升。
如果序列A已排好序,就可以将该序列的中点与v进行比较。根据比较的结果,原序列中有一半就可以不用再做进一步的考虑了。二分查找算法重复这个过程,每次都将序列剩余部分的规模减半。
用循环二分找到区间的伪代码为:
BINARY-SEARCH(A, left, right, x)
mid = ⌊(left + right) / 2⌋
return BINARY-SEARCH(A, left, mid - 1, x)
return BINARY-SEARCH(A, mid + 1, right, x)
二分算法中每一次都尽可能的分成 一个 n/2 规模的子问题 (因为二分查找中另一半不需要查找,所以规模缩小为 T ( n / 2 ) T(n/2) T ( n /2 ) 2 T ( n / 2 ) 2T(n/2) 2 T ( n /2 )
T ( n ) = T ( n / 2 ) + Θ ( 1 ) T(n) = T(n/2) + \Theta(1) T ( n ) = T ( n /2 ) + Θ ( 1 ) n log b a = n log 2 1 = 1 n^{\log_b a} = n^{\log_2 1} = 1 n l o g b a = n l o g 2 1 = 1 T ( n ) = Θ ( lg n ) T(n) = \Theta(\lg n) T ( n ) = Θ ( lg n )
我们仅仅只是优化了查找时间,我们插入的步骤还涉及到其他元素的向后移动,这个过程也是 O ( n ) O(n) O ( n ) O ( n lg n ) O(n\lg n) O ( n lg n ) 插入排序在二分查找下仍然是 Θ ( n 2 ) \Theta(n^2) Θ ( n 2 ) 。
归并排序 / Merge sort# 归并排序是分治算法的典型应用,它的时间复杂度为 O ( n lg n ) O(n\lg n) O ( n lg n )
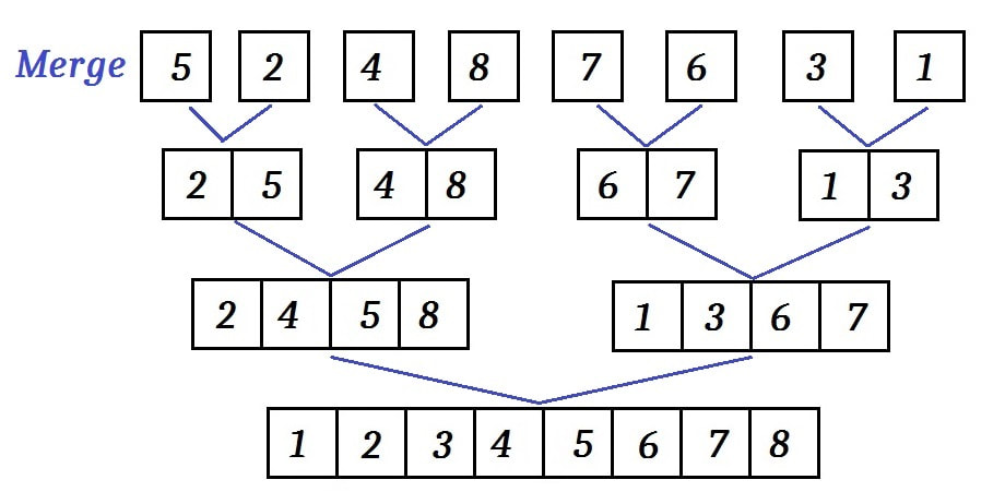
它的原理是:假如初始序列含有 n 个记录,则可以看成是 n 个有序的子序列,每个子序列的长度为 1。然后两两归并,得到 n/2 个长度为2或1的有序子序列;再两两归并,……,如此重复,直到得到一个长度为 n 的有序序列为止。
分析这个算法,若分的序列规模足够小,即 n = 1 n=1 n = 1 T ( n ) = Θ ( 1 ) T(n) = \Theta(1) T ( n ) = Θ ( 1 )
一般情况下,每次递归大致都是对半分,然后对两个一般再分,此时可以看做分为了两个规模为 n / 2 n/2 n /2 2 T ( n / 2 ) 2T(n/2) 2 T ( n /2 )
let L[0 : nL - 1] and R[0 : nR - 1] be new arrays
for i = 0 to nL - 1 //单独把左半部分放入一个数组
for j = 0 to nR - 1 //单独把右半部分放入一个数组
while i < nL and j < nR //逐位比较
if L[i] ≤ R[j] //如果左半部分这一位小于右半部分这一位
A[k] = L[i] //则把左半部分这一位放回原数组中
else A[k] = R[j] //否则放右半部分那一位
while i < nL //如果j先到了nR,即左半部分有剩余,右半部分放完了
A[k] = L[i] //把左半部分剩余的接过去
while j < nR //如果i先到了nL,即右半部分有剩余,左半部分放完了
A[k] = R[j] //把右半部分剩余的接过去
观察其合并的过程,可以知道,合并是一个逐位比较的过程,其中通过索引判断是否放完。很明显,这是个 Θ ( n ) \Theta(n) Θ ( n )
故对于归并排序:
T ( n ) = { Θ ( 1 ) i f n = 1 2 T ( n / 2 ) + Θ ( n ) i f n > 1 \begin{equation}
T(n) = \begin{cases}
\Theta(1) & if \ n=1 \\
2T(n/2) + \Theta(n) & if\ n>1
\end{cases}
\end{equation} T ( n ) = { Θ ( 1 ) 2 T ( n /2 ) + Θ ( n ) i f n = 1 i f n > 1 分析这个算法,我们可以直接使用Master method case 2,n log b a = n log 2 2 = n n^{\log_b a} = n^{\log_2 2} = n n l o g b a = n l o g 2 2 = n T ( n ) = Θ ( n lg n ) T(n) = \Theta(n\lg n) T ( n ) = Θ ( n lg n )
或者使用递归树法:
令:
T ( n ) = { c 1 i f n = 1 2 T ( n / 2 ) + c 2 n i f n > 1 \begin{equation*}
T(n) = \begin{cases}
c_1 & if \ n=1 \\
2T(n/2) + c_2n & if\ n>1
\end{cases}
\end{equation*} T ( n ) = { c 1 2 T ( n /2 ) + c 2 n i f n = 1 i f n > 1 画一个递归树
(在该图中,用 c 1 c_1 c 1 Θ ( 1 ) \Theta(1) Θ ( 1 )
我们可以从递归树中得到如下信息:
递归树深度:n / 2 d = 1 ⟹ d = lg n n/2^d = 1 \implies d = \lg n n / 2 d = 1 ⟹ d = lg n
递归树在第i层的结点数:2 i 2^i 2 i
递归树在第d层的结点数:2 d = 2 lg n = n 2^d = 2^{\lg n} = n 2 d = 2 l g n = n
对于每一层,代价之和都是 c 2 n c_2n c 2 n c 1 × n c_1 \times n c 1 × n
T ( n ) = c 2 n × ( lg n − 1 ) + c 1 n = c 2 n lg n − c 2 n + c 1 n ≤ c 2 n lg n if ( − c 2 n + c 1 n ) ≤ 0 c 2 ≥ c 1 \begin{align*}
T(n) &= c_2n \times (\lg n - 1) + c_1n \\
&= c_2n\lg n - c_2n + c_1n \\
&\le c_2n\lg n & \text{ if } (- c_2n + c_1n) \le 0 \\
& &c_2 \ge c_1
\end{align*} T ( n ) = c 2 n × ( lg n − 1 ) + c 1 n = c 2 n lg n − c 2 n + c 1 n ≤ c 2 n lg n if ( − c 2 n + c 1 n ) ≤ 0 c 2 ≥ c 1 所以,在 c 2 ≥ c 1 c_2 \ge c_1 c 2 ≥ c 1 T ( n ) = O ( n lg n ) T(n) = O(n \lg n) T ( n ) = O ( n lg n )
同理可以证出:当 0 < c 2 ≤ c 1 0 < c_2 \le c_1 0 < c 2 ≤ c 1 T ( n ) = Ω ( n lg n ) T(n) = \Omega(n\lg n) T ( n ) = Ω ( n lg n )
故最后,归并排序的时间复杂度为 T ( n ) = Θ ( n lg n ) T(n) = \Theta(n\lg n) T ( n ) = Θ ( n lg n )
快速排序 / Quicksort# 快速排序采用分治思想,一般分为三个步骤:
分解(Divide):子数组A[p...r]根据 pivot(主元)A[q] 进行分解,小于pivot的元素放到数组A[p:q-1]中, 大于pivot的元素放在A[q+1:r] 中。
解决(Conquer):通过递归调用快速排序实现对 A[p:q-1] 和 A[q+1:r] 的排序。
合并(Combine):因为子数组都是原值排序,此时 A[p:r] 有序。
于是下面就是简单的快速排序的伪代码:
这个排序中我们只做了分解这件事,此时p是起始索引,r为结束索引,q是每个划分中的pivot。接下来再对子数组进行快速排序。
接下来,就是最关键的分组:
x = A[r] //我们默认选取最后一位为pivot
i = p - 1 //i为此时lower side的最高位索引,初始化为数组0位
for j = p to r - 1 //p到r-1的元素进行分组
if A[j] ≤ x //若当前元素比pivot小
exchange A[i] with A[j] //交换位置,即把元素放到A[p:i]里面去
exchange A[i + 1] with A[r] //循环结束,把pivot放到中间去
return i + 1 // new index of pivot
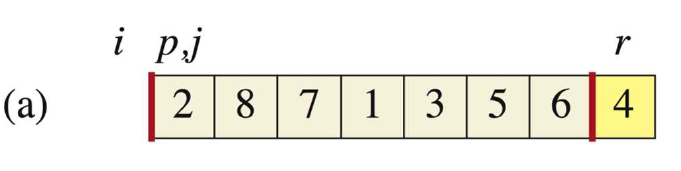
我们一步步来看这个分组部分的代码,例如数组{2,8,7,1,3,5,6,4}的第一次分组:
确定初始化i,j,r位置,i代表的是lower side的最高位索引,此时还没有则为0;j此时是位置1,r在最后。我们用浅色表示还没处理的部分。
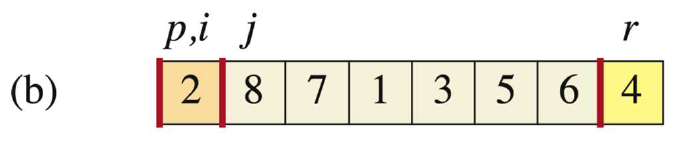
当j=1时,此时A[j]=2 < A[r],则移动i(i++到1的位置),并且让A[i]与A[j]交换,此时i=j=1,则不动。操作完后j++。我们用橙色表示比r小的部分。
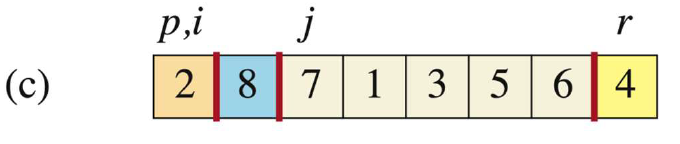
当j=2时,此时A[j]=8 > A[r],此时i不动,j++。我们用蓝色表示比r大的部分。
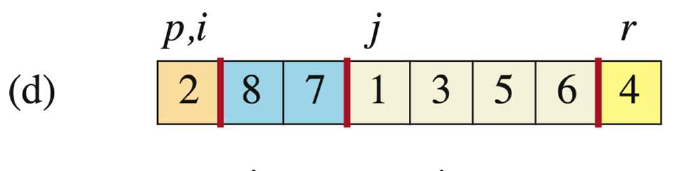
当j=3时,此时A[j]=7 > A[r],此时i不动,j++。
当j=4时,此时A[j]=1 < A[r],则移动i(i++到2的位置),并且让A[i]与A[j]交换,即A[2]与A[4]交换(2与8交换)。操作完后j++。
当j=5时,此时A[j]=3 < A[r],则移动i(i++到3的位置),并且让A[i]与A[j]交换,即A[3]与A[5]交换(3与7交换)。操作完后j++。
当j=6时,此时A[j]=5 > A[r],此时i不动,j++。
当j=7时,此时A[j]=6 > A[r],此时i不动,j++。
j=8 > p-1=7,跳出循环。把i+1位置(3+1 = 4,这是大于pivot的子数组的首元素地址)上的元素与pivot交换。(这样交换能保证pivot左边比pivot小,pivot右边比pivot大)
PARTITION 的过程中只有一个循环,很容易知道它的时间复杂度为 Θ ( n ) \Theta(n) Θ ( n )
快速排序的性能分析# 最坏情况出现在每次划分都极度不平衡时,即:
一侧子数组有 n-1 个元素
另一侧子数组有 0 个元素
例如:数组已经 完全有序 (升序或降序)、数组所有 元素相同 或每次 pivot 都是 当前子数组的最大或最小值 时出现最坏情况。
最后一层数组大小为空,则为T(0) = 0,则时间复杂度可以写为:
T ( n ) = T ( n − 1 ) + T ( 0 ) + Θ ( n ) = T ( n − 1 ) + Θ ( n ) T(n) = T(n-1) + T(0) + \Theta(n) = T(n-1) + \Theta(n) T ( n ) = T ( n − 1 ) + T ( 0 ) + Θ ( n ) = T ( n − 1 ) + Θ ( n ) 根据代入法,很容易得出它的最坏情况为 Θ ( n 2 ) \Theta(n^2) Θ ( n 2 )
猜测 T ( n ) ≤ c n 2 T(n) \leq cn^2 T ( n ) ≤ c n 2 T ( n ) = T ( n − 1 ) + d n T(n) = T(n-1) + dn T ( n ) = T ( n − 1 ) + d n
T ( n ) ≤ c ( n − 1 ) 2 + d n = c n 2 + ( d − 2 c ) n + c ≤ c n 2 if ( d − 2 c ) n + c ≤ 0 \begin{align*}
T(n) &\leq c(n-1)^2 + dn \\
&=cn^2 + (d - 2c)n + c \\
&\leq cn^2 &\text{ if } (d - 2c)n + c \le 0
\end{align*} T ( n ) ≤ c ( n − 1 ) 2 + d n = c n 2 + ( d − 2 c ) n + c ≤ c n 2 if ( d − 2 c ) n + c ≤ 0 ( d − 2 c ) n + c ≤ 0 ⟹ c ≥ d n / ( 2 n − 1 ) (d - 2c)n + c \le 0 \implies c \ge dn/(2n-1) ( d − 2 c ) n + c ≤ 0 ⟹ c ≥ d n / ( 2 n − 1 ) n ≥ 1 , c ≥ d n \ge 1, c \ge d n ≥ 1 , c ≥ d
所以,当 c ≥ d c \ge d c ≥ d T ( n ) = O ( n 2 ) T(n) = O(n^2) T ( n ) = O ( n 2 )
同理可以代入下界,有 ( d − 2 c ) n + c ≥ 0 ⟹ d − 2 c ≥ 0 ⟹ c ≤ d / 2 (d - 2c)n + c \ge 0 \implies d - 2c \ge 0 \implies c \le d/2 ( d − 2 c ) n + c ≥ 0 ⟹ d − 2 c ≥ 0 ⟹ c ≤ d /2
所以,当 c ≤ d / 2 c \le d/2 c ≤ d /2 T ( n ) = Ω ( n 2 ) T(n) = \Omega(n^2) T ( n ) = Ω ( n 2 )
此时最坏情况为 T ( n ) = Θ ( n 2 ) T(n) = \Theta(n^2) T ( n ) = Θ ( n 2 )
而快速排序最好的情况是在 最平衡的划分 ,即:
两侧子数组大小相等(或相差1)
pivot 正好是中位数
两个子问题都不大于n/2,均可看成对半划分,则 T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n) = 2T(n/2) + \Theta(n) T ( n ) = 2 T ( n /2 ) + Θ ( n )
根据Master method,n log b a = n log 2 2 = n n^{\log_b a} = n^{\log_2 2} = n n l o g b a = n l o g 2 2 = n Θ ( n lg n ) \Theta(n \lg n) Θ ( n lg n )
此外,到一般的情况情况下,快速排序的平均情况的运行时间更接近于最好情况的运行时间 ,而不是最坏情况的运行时间之间。
在平均情况下,好的划分和坏的划分是随机分布的,假设好的划分是最好情况划分,坏的情况是最坏情况划分,当好坏划分交替出现时,一个坏的划分和一个好的划分等价于一个好的划分,所以,快速排序的平均情况的运行时间很可能是 O ( n lg n ) O(n\lg n) O ( n lg n )
随机快速排序# 与始终采用 A[r] 作为主元的方法不同,随机快速排序是从子数组 A[p..r] 中 随机选择一个元素作为主元 。我们称其为随机抽样(random sampling)。
为达到这一目的,首先将 A[r](最后一位)与从 A[p..r] 中随机选出的一个元素 交换 。通过对序列 A[p..r] 的随机抽样,我们可以保证主元元素 x=A[r] 是等概率地从子数组的 r-p+1 个元素中选取的。
我们修改一下我们的快速排序即可:
exchange A[i + 1] with A[r]
RANDOMIZED-PARTITION(A, p, r)
return PARTITION(A, p, r)
RANDOMIZED-QUICKSORT(A, p, r)
q = RANDOMIZED-PARTITION(A, p, r)
RANDOMIZED-PARTITIONQUICKSORT(A, p, q - 1)
RANDOMIZED-PARTITIONQUICKSORT(A, q + 1, r)
RANDOMIZED-PARTITION 将任意常数比例的元素划分到一个子数组中。则算法的递归树的深度为 Θ ( lg n ) \Theta(\lg n) Θ ( lg n ) O ( n ) O(n) O ( n ) O ( n lg n ) O(n\lg n) O ( n lg n )
最坏情况下,RANDOMIZED-PARTITION 被调用 T ( n ) = T ( n − 1 ) + 1 T(n) = T(n-1) + 1 T ( n ) = T ( n − 1 ) + 1 T ( n ) = Θ ( n ) T(n) = \Theta(n) T ( n ) = Θ ( n ) 不会 使得快速排序的最坏情况运行时间更优。
最好情况下,与快速排序相同,RANDOMIZED-PARTITION 被调用 T ( n ) = 2 T ( n / 2 ) + 1 T(n) = 2T(n/2) + 1 T ( n ) = 2 T ( n /2 ) + 1 T ( n ) = Θ ( n ) T(n) = \Theta(n) T ( n ) = Θ ( n )
最好情况和最坏情况RANDOMIZED-PARTITION被调用次数都是 Θ ( n ) \Theta(n) Θ ( n )
快速选择算法 / Quick Select# 基于随机快速排序,有一种期望为线性时间 ( Θ ( n ) \Theta(n) Θ ( n ) 选择算法 - RANDOMIZED-SELECT。
RANDOMIZED-SELECT(A,p,r,i) 将找到并返回数组 A[p..r] 中第 i 小的元素。并不需要排序所有的元素,而是找到第 i 小的元素。
它的思路也很简单:我们知道快速排序算法中经过 PARTITION 划分得到 A[p..q-1] 和 A[q+1..r] 两个子数组,以及主元 A[q] 的位置。接下来再递归地去处理 A[p..q-1] 和 A[q+1..r] 中的元素,并找到它们的主元。
划分结束后的主元位置将不会被改变 ,因为 A[p..q-1] 中都是比 A[q] 小的元素,A[q+1..r] 中都是比 A[q] 大的元素。
于是,我们就可以在这里找到第 i 小的元素,而不需要完全处理完划分。
所以这个选择算法又称为 快速选择算法 。下面是它的伪代码:
exchange A[i + 1] with A[r]
RANDOMIZED-PARTITION(A, p, r)
return PARTITION(A, p, r)
RANDOMIZED-SELECT(A, p, r, i)
q = RANDOMIZED-PARTITION(A, p, r)
return A[q] // the pivot value is the answer
return RANDOMIZED-SELECT(A, p, q - 1, i)
else return RANDOMIZED-SELECT(A, q + 1, r, i - k)
接下来通过一个例子去展示它的运行过程:
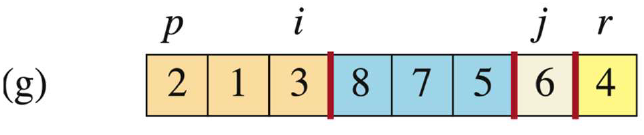
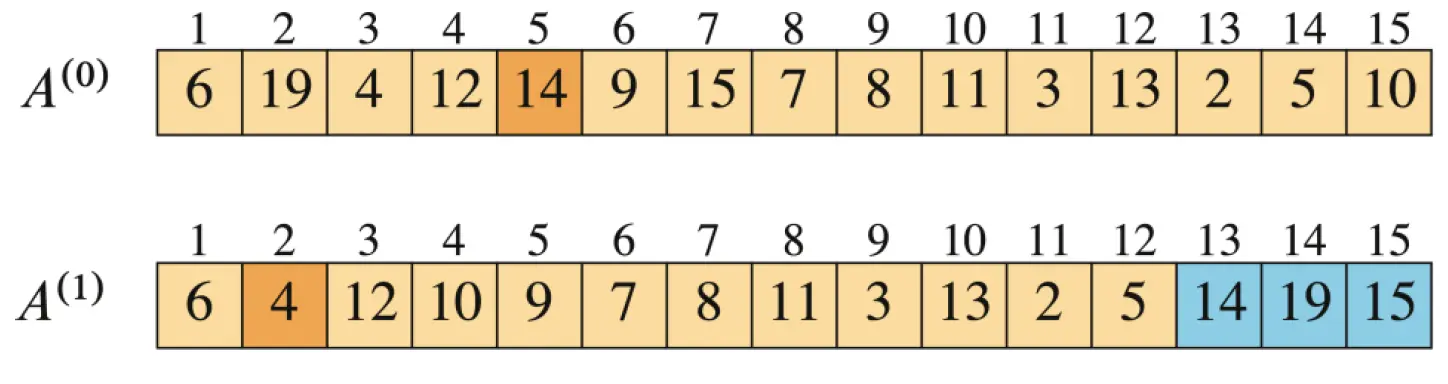
假设 A = [6, 19, 4, 12, 14, 9, 15, 7, 8, 11, 3, 13, 2, 5, 10] (索引从1开始),需要找到最小的第 5 个数。
初始状态下,调用:RANDOMIZED-SELECT(A, 1, 15, 5) 并且递归调用 RANDOMIZED-PARTITION 选中的主元为 14,并将它与 A[15] 交换位置。
第一次 RANDOMIZED-PARTITION 调用 PARTITION,得到如下的状态:
其中:浅色部分为当前轮次中参与 PARTITION 的数组元素,加深的元素表示 RANDOMIZED-PARTITION 选中的下一次 PARTITION 的主元。蓝色部分的元素表示不参与下一次 PARTITION 的元素,因为需要选择的 i 不在蓝色的范围内。
q = 13, 因此,下次将处理 A[1,12],继续找第 5 个数。
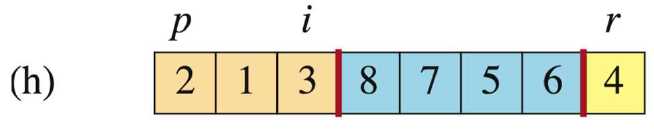
第二次 RANDOMIZED-PARTITION 交换主元后调用 PARTITION,得到如下情况:
q = 3,接下来处理 A[4,12],继续找第 5 - 3 = 2 个数。
接下来的情况同理,直到剩余的元素已经全部处理完毕,返回第 5 个数。
接下来我们分析这个算法。如果每次划分枢轴都很不巧地选择了剩余元素中的最大值就会出现 最坏情况 ,此时划分序列恰为输入序列的 降序排序 。
此时运行时间和快速排序的最坏情况一样,递归式为 T ( n ) = T ( n − 1 ) + Θ ( n ) = Θ ( n 2 ) T(n) = T(n-1) + \Theta(n) = \Theta(n^2) T ( n ) = T ( n − 1 ) + Θ ( n ) = Θ ( n 2 )
RANDOMIZED-SELECT 在平均情况下的期望时间为 Θ ( n ) \Theta(n) Θ ( n )
Exercises in Sort Methods#
有一种排序算法叫 Stooge-Sort,以喜剧团队“三个臭皮匠”的名字命名。
then exchange A[i] <-> A[j]
(a). 请给出 STOOGE-SORT 最坏情况运行时间的递归式及其解。
(b). 将 STOOGE-SORT 的最坏情况运行时间与插入排序、归并排序和快速排序进行比较,并给出结论。
这一题给出了一个排序算法的伪代码,需要我们分析代码得到递归式,并应用解递归式的方法来求解最坏情况运行时间。
观察伪代码可以发现,这个算法是递归的,并且每次递归调用都会产生三个新的递归调用。此外,一次调用中的运行时间代价为 Θ ( 1 ) \Theta(1) Θ ( 1 )
根据我们的经验,最坏的情况一般发生在已经有序的时候。我们代入一些数据来看看递归的规模如何,例如 A = [1,2,3,4,5,6,7,8,9,10] (以1为起始索引) STOOGE-SORT(A, 1, 10)
若 A[1] > A[10] 则交换 A[1] 和 A[10],这里无事发生。
若 i + 1 >= 10 则返回,这里是检测是否结束递归。
k <- ⌊(10-1+1)/3⌋ = 3 取了三分位数。递归调用 STOOGE-SORT(A, 1, 7),这里将递归排序三分之二的值。
递归调用 STOOGE-SORT(A, 4, 10),这里将递归排序三分之二的值。
递归调用 STOOGE-SORT(A, 1, 7),这里将递归排序三分之二的值。
那么我们可以得出结论,每次递归调用的规模是父递归调用的 2 / 3 2/3 2/3
T ( n ) = 3 T ( 2 n / 3 ) + Θ ( 1 ) T(n) = 3T(2n/3) + \Theta(1) T ( n ) = 3 T ( 2 n /3 ) + Θ ( 1 ) 解这样的递归式我们可以使用主方法 Case 1:分水岭函数为 n log 3 2 3 n^{\log_{\frac{3}{2}}3} n l o g 2 3 3 f ( n ) = Θ ( 1 ) = n 0 f(n) = \Theta(1) = n^0 f ( n ) = Θ ( 1 ) = n 0
显然,log 3 2 3 > 0 ⟹ n log 3 2 3 > n 0 ⟹ T ( n ) = Θ ( n log 3 2 3 ) \log_{\frac{3}{2}}3 > 0 \implies n^{\log_{\frac{3}{2}}3} > n^0 \implies T(n) = \Theta(n^{\log_{\frac{3}{2}}3}) log 2 3 3 > 0 ⟹ n l o g 2 3 3 > n 0 ⟹ T ( n ) = Θ ( n l o g 2 3 3 )
此时存在 ϵ = 3 > 0 \epsilon = 3 > 0 ϵ = 3 > 0 f ( n ) = O ( n log 3 2 3 − 3 ) = O ( 1 ) f(n) = O(n^{\log_{\frac{3}{2}}3-3}) = O(1) f ( n ) = O ( n l o g 2 3 3 − 3 ) = O ( 1 )
题目还要求我们对比该算法与插入排序、归并排序和快速排序的最坏情况运行时间:
插入排序最坏情况运行时间:T ( n ) = Θ ( n 2 ) T(n) = \Theta(n^2) T ( n ) = Θ ( n 2 )
归并排序最坏情况运行时间:T ( n ) = Θ ( n lg n ) T(n) = \Theta(n \lg n) T ( n ) = Θ ( n lg n )
快速排序最坏情况运行时间:T ( n ) = Θ ( n 2 ) T(n) = \Theta(n^2) T ( n ) = Θ ( n 2 )
因为 log 3 2 3 > log 3 2 9 4 = 2 \log_{\frac{3}{2}}3 > \log_{\frac{3}{2}}\frac{9}{4} = 2 log 2 3 3 > log 2 3 4 9 = 2 Stooge-Sort 的最坏情况运行时间比插入排序、归并排序和快速排序要长。
如果在归并排序中对小数组 (长度为k) 采用插入排序,找到在最坏情况下合并子表的运行时间表达式,并且找到如何采用合适的参数 k 使得修改后的归并排序运行时间与原本的归并排序运行时间相同。
虽然插入排序的最坏情况运行时间 Θ ( n 2 ) \Theta(n^2) Θ ( n 2 ) Θ ( n lg n ) \Theta(n\lg n) Θ ( n lg n ) Θ ( n ) \Theta(n) Θ ( n )
所以我们可以用插入排序修改归并排序的递归树。使其不要到只有一个元素再进行合并,而是到一个设定的数组长度时,最小的子数组(归并段)执行插入排序,设最小子数组(归并段)长度为 k ,分成 n/k 个子数组(归并段)。
插入排序对它最快 Θ ( k ) × ( n / k ) = Θ ( n ) \Theta(k) \times (n/k) = \Theta(n) Θ ( k ) × ( n / k ) = Θ ( n ) Θ ( k 2 ) × ( n / k ) = Θ ( n k ) \Theta(k^2) \times (n/k) = \Theta(nk) Θ ( k 2 ) × ( n / k ) = Θ ( nk )
对于归并排序:
T ( n ) = { Θ ( 1 ) i f n = 1 2 T ( n / 2 ) + Θ ( n ) i f n > 1 \begin{equation}
T(n) = \begin{cases}
\Theta(1) & if \ n=1 \\
2T(n/2) + \Theta(n) & if\ n>1
\end{cases}
\end{equation} T ( n ) = { Θ ( 1 ) 2 T ( n /2 ) + Θ ( n ) i f n = 1 i f n > 1 它的递归树:
根据设定,我们把原数组分成 n/k 个子数组时停止划分,此时递归树在深度 h 层时,规模变成 n / k n/k n / k n k × 2 h = 1 ⟹ h = lg ( n / k ) \frac{n}{k \times 2^h} = 1 \implies h = \lg(n/k) k × 2 h n = 1 ⟹ h = lg ( n / k )
递归树每一层合并时间为 Θ ( n ) \Theta(n) Θ ( n ) h 层的合并一共耗费时间:Θ ( n ) × lg ( n / k ) = Θ ( n lg ( n / k ) ) \Theta(n) \times \lg(n/k) = \Theta(n\lg(n/k)) Θ ( n ) × lg ( n / k ) = Θ ( n lg ( n / k ))
则此时把它们时间合并起来,可以得到归并排序下使用插入排序的时间。若以最坏的情况来看:Θ ( n lg ( n / k ) ) + Θ ( n k ) = Θ ( n k + n lg ( n / k ) ) \Theta(n\lg(n/k)) + \Theta(nk) = \Theta(nk + n\lg(n/k)) Θ ( n lg ( n / k )) + Θ ( nk ) = Θ ( nk + n lg ( n / k ))
Θ ( n k + n lg ( n / k ) ) = Θ ( n k + n lg n − n lg k ) = Θ ( n k + n lg n ) since Θ ( n k ) ≥ Θ ( n lg k ) \begin{align*}
&\Theta(nk + n\lg(n/k)) \\
&=\Theta(nk + n\lg n - n\lg k) \\
&=\Theta(nk + n\lg n) & \text{ since } \Theta(nk) \ge \Theta(n\lg k)
\end{align*} Θ ( nk + n lg ( n / k )) = Θ ( nk + n lg n − n lg k ) = Θ ( nk + n lg n ) since Θ ( nk ) ≥ Θ ( n lg k ) 要维持或优于标准的归并排序,我们需要 Θ ( n k + n lg n ) ≤ Θ ( n lg n ) \Theta(nk + n\lg n) \le \Theta(n\lg n) Θ ( nk + n lg n ) ≤ Θ ( n lg n ) n k ≤ n lg n ⟹ n ≤ lg n nk \le n\lg n \implies n \le \lg n nk ≤ n lg n ⟹ n ≤ lg n k = Θ ( lg n ) k = \Theta(\lg n) k = Θ ( lg n )
所以 k k k k = c lg n , c > 0 k=c\lg n,\ c>0 k = c lg n , c > 0
Mendel 教授提议通过取消对i和k是否相等的检查来简化RANDOMIZED-SELECT。简化后的程序称为SIMPLER-RANDOMIZED-SELECT。
SIMPLER-RANDOMIZED-SELECT(A, p, r, i)
q = RANDOMIZED-PARTITION(A, p, r)
return SIMPLER-RANDOMIZED-SELECT(A, p, q, i)
else return SIMPLER-RANDOMIZED-SELECT(A, q+ 1, r, i-k)
证明 SIMPLER-RANDOMIZED-SELECT 算法在最坏情况下永远不会终止 (死循环)。
我们分析这个代码可以得到:如果在第一次调用 RANDOMIZED-PARTITION 时得到 q = r,则说明数组里全是比 A[q] 小的数,此时取到了最大值,是最坏的情况。
k = q - p + 1 = r,此时进入下个 SIMPLER-RANDOMIZED-SELECT 递归时数组的区间没有任何改变。在最坏的情况下会一直选到最大值,重复这一过程,相当于进行无限递归,程序死循环。