
Introduce
蓄水池算法 (Reservoir Sampling) 是一种处理流式数据的随机采样问题的高效算法。它可以处理数据量巨大、或者数据动态生成的采样情况,并可以保证每个样本被抽中的概率相等。本章记录了我学习蓄水池算法的一些笔记。
Principle
蓄水池算法的目标是解决如下的问题:
假设有一个数据集长度为 ,,计算机无法将 个元素全部加载都内存中。我们需要从数据集中抽取 个元素,要求满足:
- 每个元素只能访问一次。
- 每个元素采样概率相等。
蓄水池算法的基本思路是:
- 维护一个容量为
K的数组reservoir[K],用于存储抽取的元素。 - 对于第
i个数据集中的元素,执行如下分类操作:- (初始化) 如果
i < K,则将该元素加入采样池reservoir[i]中。 - (替换) 如果
i >= K,则随机生成一个数r (0 ≤ r ≤ i),若r < K,则将reservoir[r]替换为当前元素;若r >= K,则不替换。
- (初始化) 如果
- 抽取结束后,数组
reservoir[K]为最终的采样结果。
我们通过如下一个例子来解释这个算法的过程:
假设有一个数据集
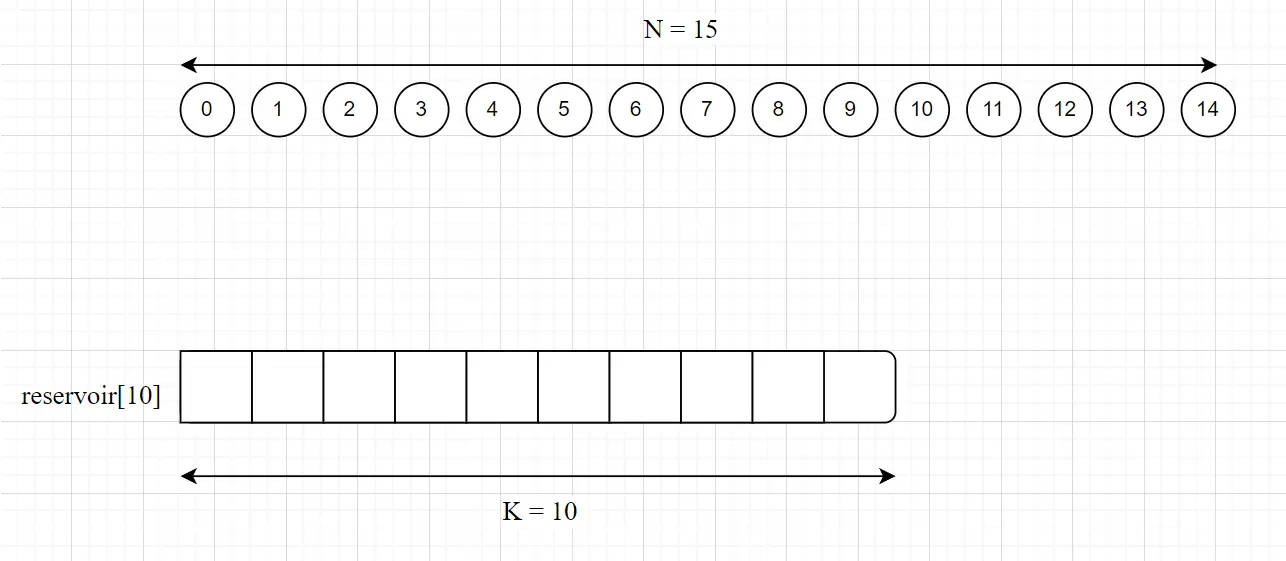
stream长度为 ,数据集为:[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]。我们希望随机采样 个元素。
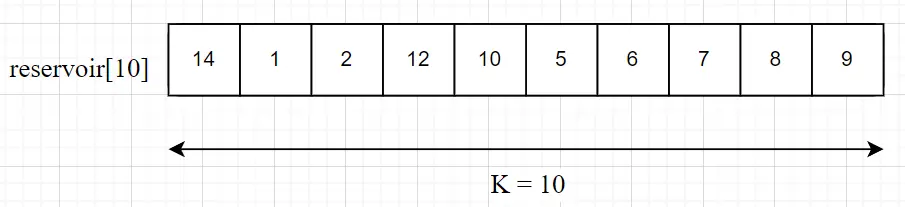
- 维护一个容量为
K的数组reservoir[10]。
-
对于第
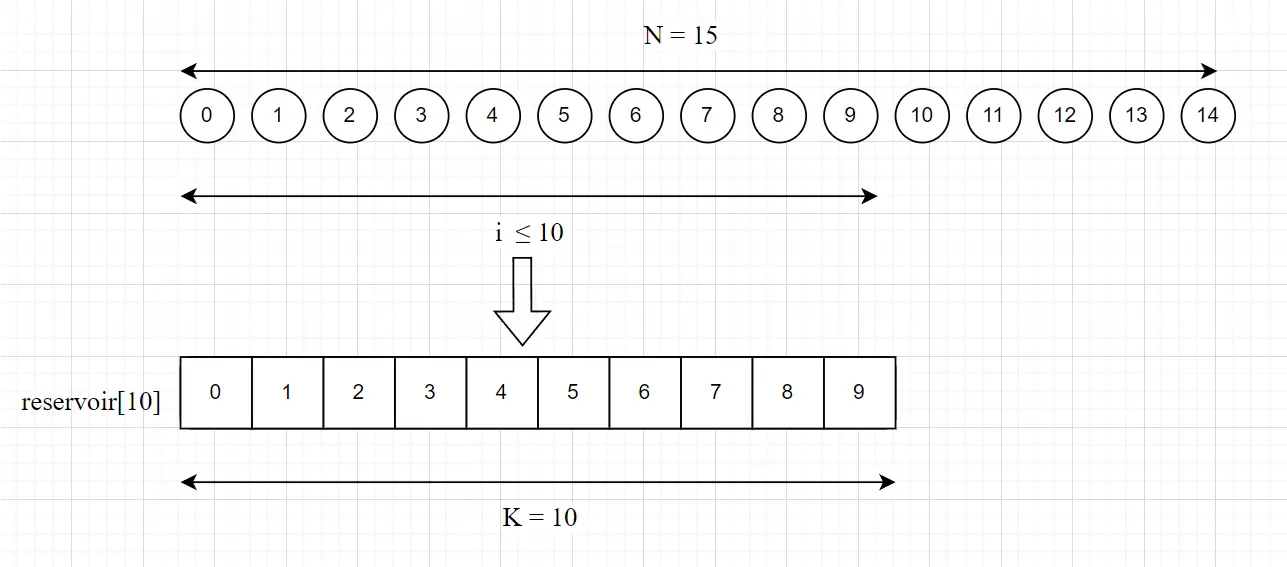
i个数据集中的元素,执行如下分类操作:- (初始化) 如果
i < 10,则将该元素加入采样池reservoir[i]中。我们将数据集的前 10 个元素加入reservoir[0]到reservoir[9]中。
- (替换) 如果
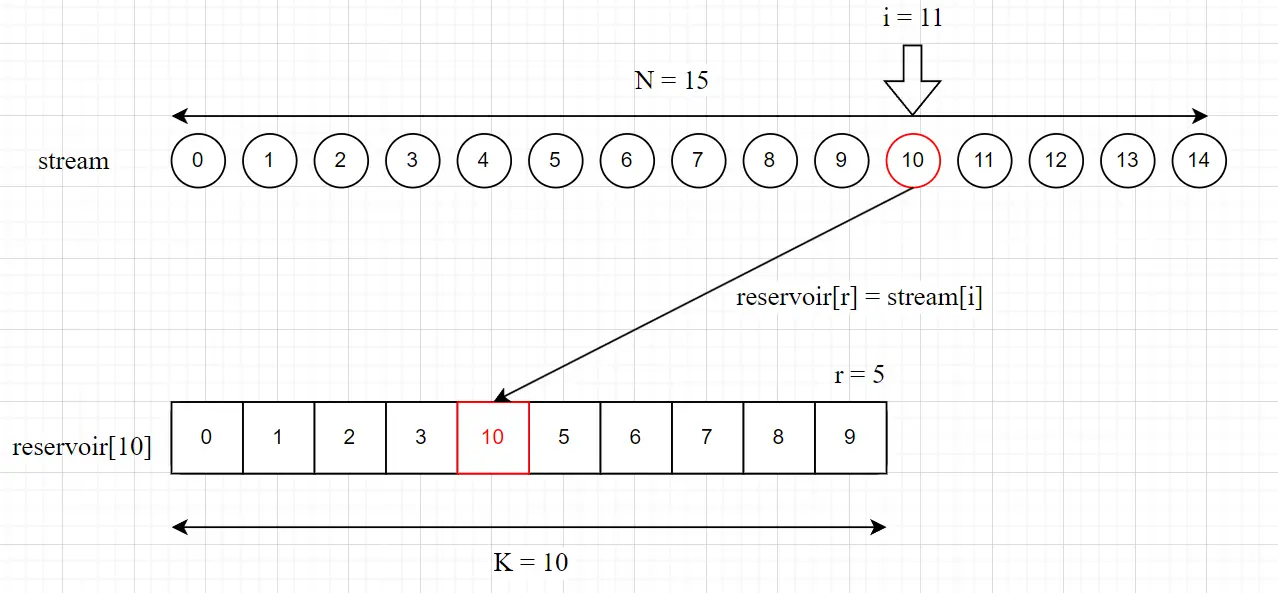
i >= 10,则随机生成一个数r (0 ≤ r ≤ i),若r < 10,则将reservoir[r]替换为当前元素;若r >= 10,则不替换。
假设i = 11,r = 5,r < 10, 则reservoir[r] = stream[i], 即reservoir[5]被替换为stream[11]。
假设
i = 12,r = 11,r > 10, 则不发生与采样池的替换。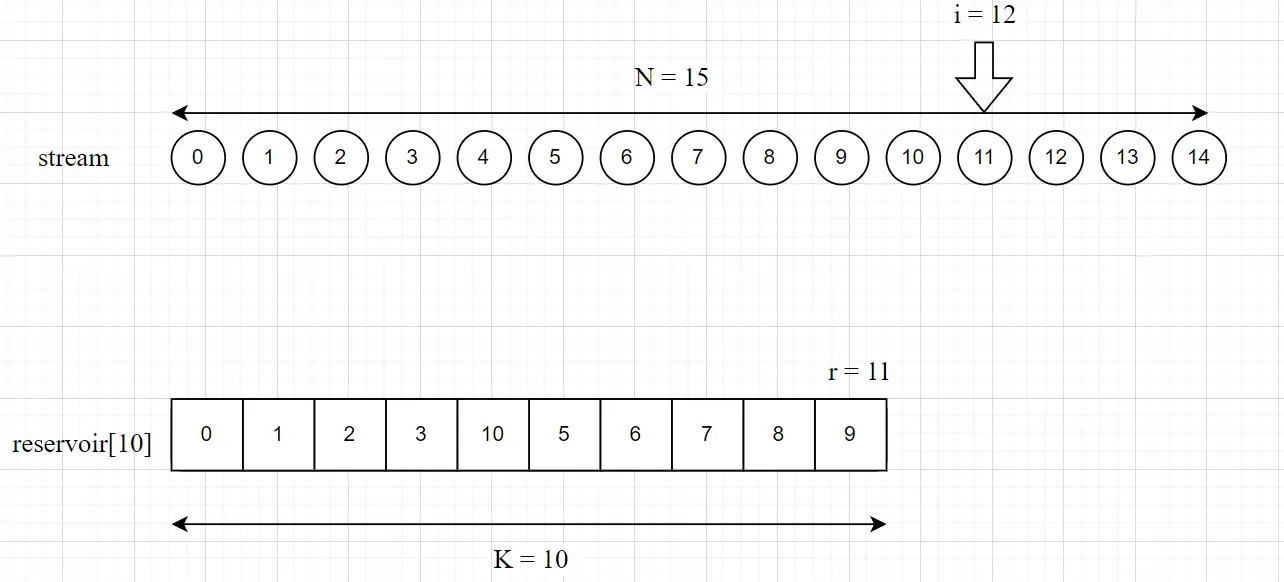
- (初始化) 如果
-
抽取结束后,数组
reservoir为最终的采样结果。
Code
实现这样的蓄水池算法很简单,接下来通过一个Python代码来演示。
- 创建一个函数
reservoir_sampling,接收两个参数stream和K,返回一个长度为K的列表reservoir。 - 遍历数据集
stream,对每个元素执行分类操作。- 如果
i < K,则将该元素加入采样池reservoir[i]中。 - 如果
i >= K,则随机生成一个数r (0 ≤ r ≤ i),若r < K,则将reservoir[r]替换为当前元素;若r >= K,则不替换。
- 如果
- 返回最终的采样结果
reservoir。
import randomdef reservoir_sampling(stream, K): reservoir = []
for i, item in enumerate(stream): if i < K: reservoir.append(item) continue r = random.randint(0, i) if r < K: reservoir[r] = item
return reservoir我们可以对当前算法进行一些简单的测试:
# 从 100 个元素中随机抽取 10 个stream = [i for i in range(100)]sample_k10 = reservoir_sampling(stream, 10)Proof
你可能比较好奇为什么蓄水池算法能保证每个元素被抽中的概率相等。接下来是它的数学证明部分。
我们将其问题转化为数学式:
设数据集的长度为 ,需要抽取 个元素,求证:每个元素被抽中的概率为 。
在初始化阶段,第 个元素一定会被蓄水池采样,此时被抽样的概率 。在初始化结束后,若 , 则对于第 个元素,被抽中的概率为:
根据算法,第 个元素会被选入蓄水池的条件是:生成一个 到 的随机数 ,且 。
生成随机数的总可能性有 种 (从 到 ), 使得第 个元素被选中的情况有 种 ()。
所以,第 个元素被选入蓄水池的概率是:
选中后,它会随机替换蓄水池中 个位置之一。对于任意一个已经在蓄水池中的旧元素 ,它在处理第 步时仍在蓄水池中。
那么,元素 在第 步之后 仍然留在蓄水池 中的概率,可以分为两个事件:
- 在处理第 步之前, 就在蓄水池中。
- 在处理第 步时, 没有被替换。
对于事件 1, 要继续留在蓄水池中,必须满足: 在处理第 步时,它没有被第 个元素替换。
我们可以使用数学归纳法来继续证明。根据我们的归纳假设,在处理第 步时,满足公式 (1),元素 在蓄水池中的概率是:
对于事件 2, 在处理第 步时没有被替换,有两种可能,它们之间是 或 的关系:
-
第 个元素根本没被选中进入蓄水池。 这个概率是:1 - P(第 i 个元素被选中),即:
-
第 个元素被选中进入蓄水池,但被蓄水池中的其他元素替换,即 ,这种情况的概率也很明显是 第 个元素被选中的概率 没选中 的概率。
因此,元素 在第 步后继续留在蓄水池中的总概率是事件 1 和事件 2 同时成立的概率:
由公式 (1)、(3)、(6) 可以判定:对于任意一个元素 ,它被抽中 (留在蓄水池) 中的概率为 。
这个结论可以从 一直推广到 。因此,当算法处理完所有 个元素后,数据集中任意一个元素最终留在蓄水池中的概率都是 。
Summary
蓄水池算法是一种高效的随机抽取算法,它通过维护一个固定大小的数组来保存数据集的随机子集。它可以解决 数据集过大无法全部加载进内存的问题,并 保持抽取的概率与数据集的概率一致。
Reference
[1]. Reservoir Sampling
[2]. 蓄水池抽样算法——原理、实现与应用
[3]. Reservoir Sampling

