What is Learning?#

学习，从最简单的角度理解，就是通过经验来获得知识或者技能的过程。机器学习就是让机器（计算机）也能向人类一样，通过观察大量的数据和训练，发现事物规律，获得某种分析问题、解决问题的能力。

以下是一些重要的基本术语：

• 输入空间 (Input Space)：这是所有可能的输入值的集合。例如，如果我们用年龄和收入来预测是否发放信用卡，那么所有可能的年龄和收入的组合就构成了输入空间。
• 输出空间 (Output Space)：这是模型可能输出的所有结果的集合。例如，对于判断是否发放信用卡的问题，输出空间就是“发放”和“不发放”这两个结果。
• 目标函数 (Target Function)：这是一个理想的函数，它能够准确地将输入映射到正确的输出。在实际中，我们通常不知道这个目标函数是什么。
• 数据集 (Dataset)：这是我们用来训练模型的数据集合，通常包含一些输入和对应的正确输出。
• 假设 (Hypothesis)：这是一个模型，我们用它来尝试逼近目标函数。
• 假设集 (Hypothesis Set)：在进行机器学习之前，预先设定的所有可能的模型表达式的集合。
• 学习算法 (Learning Algorithm)：这是一个用来从假设集中选择最佳假设的方法。
• 最终选择的假设 (Final Hypothesis, g)：这是通过学习算法从假设集中选出的，最接近目标函数的假设。

机器学习的流程图可以表示为：

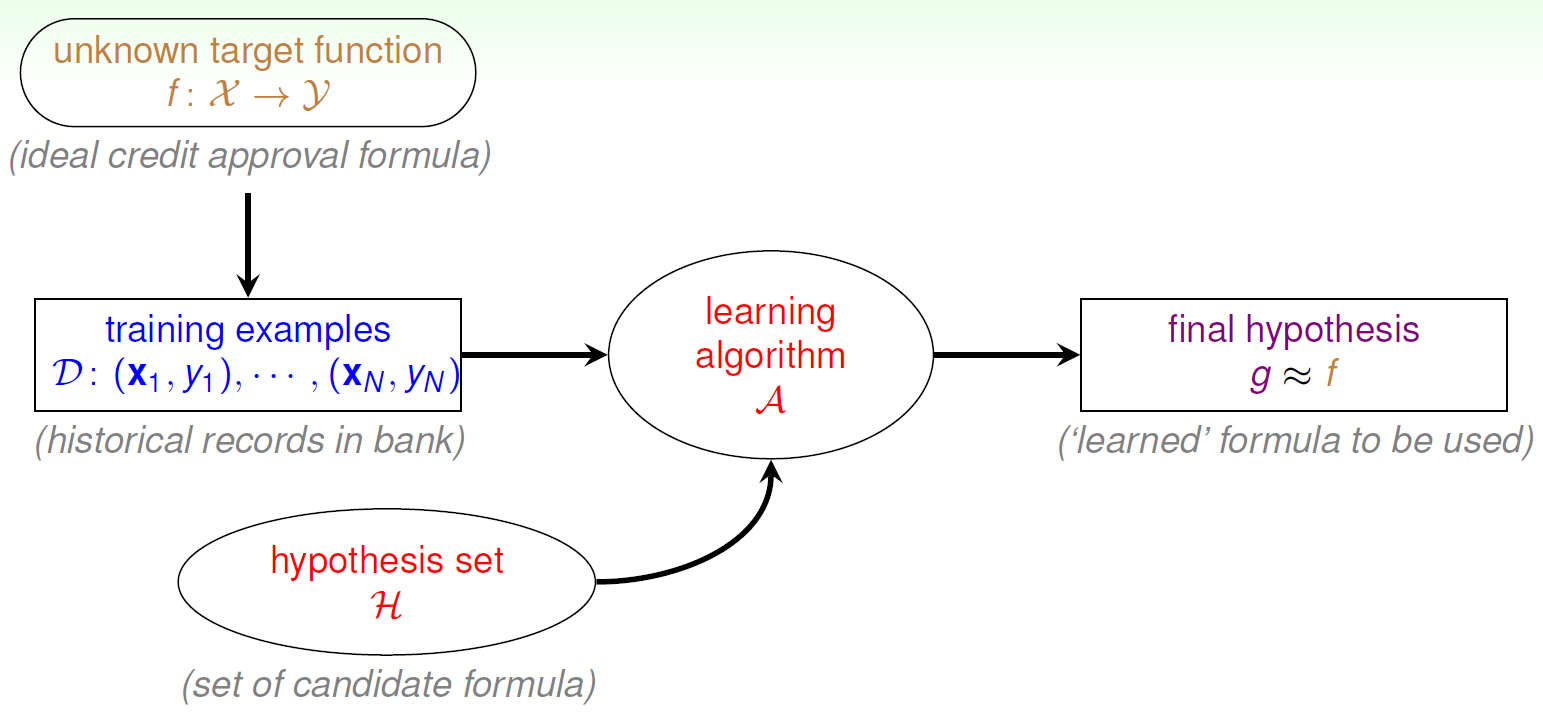
对于理想的目标函数$f$，我们是不知道的，我们只有训练数据集$D$。

机器学习的过程就是使用根据实际情况和知识假设的假设集(hypothesis set) $\mathcal{H}$，通过机器学习算法 $A$，在训练样本 $D$ 上进行训练，选择出一个最好的假设hypothes，使得当前模型训练函数表达式 $g$ 最接近目标函数 $f$ 。

学习可以分成很多类，根据我们希望模型预测的输出类型，可以将机器学习分为以下几种：

• 二元分类 (Binary Classification)：输出空间 $Y = \{-1, +1\}$ 或者 $\{0, 1\}$。模型需要判断输入属于两个类别中的哪一个。 例如，判断邮件是否为垃圾邮件。

• 多元分类 (Multiclass Classification)：输出空间 $Y = \{1, 2, ..., K\}$，其中 $K > 2$。模型需要判断输入属于多个类别中的哪一个。 例如，识别图片中的物体是猫、狗还是鸟。

• 回归 (Regression)：输出空间 $Y = \mathbb{R}$ （实数）。模型需要预测一个连续的数值。例如，预测房价或者股票价格。

• 结构化学习 (Structured Learning)：输出空间 $Y$ 是结构化的对象，例如序列、树或图。模型需要预测一个复杂的结构。例如，词性标注，将句子中的每个词标注其词性（名词、动词等）

根据训练数据中是否包含标签信息，可以将机器学习分为：

• 监督学习 (Supervised Learning)：训练数据包含输入特征 $x_n$ 和对应的标签 $y_n$。我们通过学习输入和输出之间的映射关系来进行预测。 例如，使用带有标签的图片训练一个图像分类器。

• 无监督学习 (Unsupervised Learning)：训练数据只有输入特征 $x_n$，没有对应的标签。模型需要在数据中发现模式和结构。例如，聚类算法将用户分组。

• 半监督学习 (Semi-supervised Learning): 训练数据中一部分有标签，一部分没有标签。模型可以利用有标签数据和无标签数据来提升学习效果。

• 强化学习 (Reinforcement Learning)：模型通过与环境的交互来学习。模型执行动作并接收奖励或惩罚，从而学习到最优策略。例如，训练一个玩游戏的 AI。

Perceptron Learning Algorithm (PLA)#

感知机学习算法 (PLA) 是一种用于解决二元分类问题的简单而有效的算法。

它的目标是找到一个超平面（在二维空间中就是一条直线）来将两类不同的数据点分开。数据点被标记为两类，比如 “+1” 和 “-1”，PLA 的任务就是找到一条线，使得所有标记为 “+1” 的点都在线的一侧，而所有标记为 “-1” 的点都在另一侧。

输入数据可以表示为特征向量，模型通过调整这些特征的权重来做出分类决策。我们称这样的模型为感知机模型 (perceptron model).

其中，sign函数是符号函数，是一个逻辑函数，用以判断实数的正负号。相当于是将一个线性回归问题映射到了二元分类上。

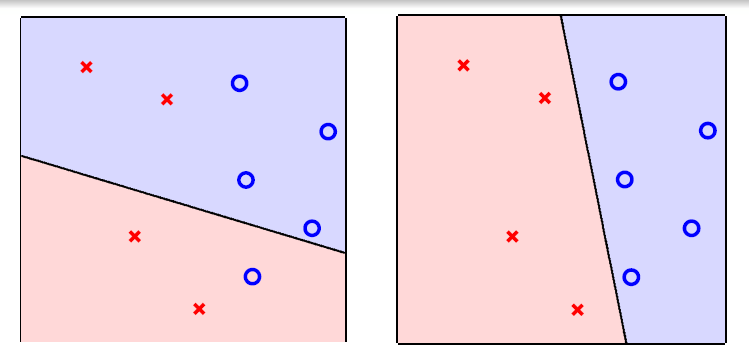
PLA 的核心思想是通过不断地纠正错误来逐步找到这条最佳的分割线。它的工作流程大致如下：

1. 初始化：首先，我们需要一个初始的分割线。这通常是通过随机选择一个权重向量 $(w)$ 来实现的，或者简单地将其设为零向量。
2. 寻找错误点: 接下来，我们遍历数据集中的每一个数据点，看看当前的分割线是否能正确地对其进行分类。 如果一个数据点被错误地分类了，我们就找到了一个“错误点”。
3. 修正分割线：一旦找到一个错误点，我们就根据这个错误点的信息来调整我们的分割线。具体的调整方法是更新权重向量 $(w)$。如果一个本应是 “+1” 的点被错误地分到了 “-1” 那一侧，我们就调整 $(w)$ 使得分割线向这个点的方向靠近。反之，如果一个本应是 “-1” 的点被错误地分到了 “+1” 那一侧，我们就调整 $w$ 使得分割线向远离这个点的方向移动。 这个调整可以用一个简单的公式表示：$(w_{t+1} \leftarrow w_t + y_n(t)x_n(t))$，其中 $(w_t)$ 是当前的权重向量，$(y_n(t))$ 是错分类错误点的真实标签，$(x_n(t))$ 是错分类错误点的特征向量。
4. 重复迭代： 我们不断重复步骤 2 和 步骤 3，也就是持续地寻找错误点并修正分割线，直到数据集中的所有点都被正确分类为止。

需要注意的是，PLA 有一个重要的前提条件：数据集必须是线性可分的。必须存在一条完美的直线（或超平面）能够将两类数据完全分开。如果数据集不是线性可分的，PLA 可能陷入死循环。在后续的章节中我们会详细解释PLA算法的过程。

Feasibility of Learning#

我们用 PLA 在一些已有的数据点上找到了一条完美的分割线。这条线在这些已知的数据上表现得非常好，能够完美地将两类数据分开。但是，我们如何才能确信，这条线对于我们从未见过的新数据点也同样有效呢？ 这就是“可行性”要解决的问题：我们凭什么相信，通过在已知数据上学习到的模型，能够很好地预测未知的数据呢？

一个非常重要的理论就是所谓的 “没有免费的午餐”定理 (No Free Lunch Theorem, NFL)，它告诉我们：不存在一个通用的机器学习算法，能够在所有可能的问题上都表现最好。

对于某个特定的问题 A，算法 X 可能表现得非常出色；但是对于另一个完全不同的问题 B，算法 X 的表现可能还不如随机猜测。反过来，可能存在另一个算法 Y，在问题 B 上表现优异，但在问题 A 上却很糟糕。如果我们不对要解决的问题做任何假设，不对数据的分布有任何先验的了解，那么我们不可能找到一个在所有情况下都有效的“万能”学习算法。我们必须根据具体的问题来选择合适的模型和算法。

那么 在面对一个特定的问题时，我们应该如何做出选择？ 这就引出了 假设集 (Hypothesis Set) 的概念：

假设集 $\mathcal{H}$ 就是我们用来解决问题的所有可能的模型的集合。例如，如果我们使用 PLA，那么 $\mathcal{H}$ 就是所有可能的分割直线的集合。

但在具体情况中，假设集 $\mathcal{H}$ 可能很大。可能性越多，我们就越有可能在训练数据上找到一个表现“完美”的模型，即碰巧找到了在训练数据上表现得很好的模型。这个模型可能并没有真正学到数据背后的规律，因此在面对新的、未知的数据时，它的表现就会很差。

为了量化这种“坏的泛化 (Bad Generalization)”发生的概率，我们使用一些统计学习理论的方法去衡量。霍夫丁不等式 (Hoeffding’s Inequality) 是一种用来估计这种概率的工具，它告诉我们，对于一个固定的假设 $h$，训练误差 $E_{in}(h)$ 与真实误差 $E_{out}(h)$ 之间偏差很大的概率是有限的，并且会随着训练数据量的增加而减小。

• $P[|E_{in}(h) - E_{out}(h)|$ 表示的是 “存在一个坏的假设”的概率 ，即那些在训练数据上表现很好（$E_{in}$ 很小），但在真实数据上表现很差（$E_{out}$ 很大）的假设。
• $2Me^{-2\epsilon^2N}$ 给出了这个概率的上界。
  • $M$：假设集的大小。$M$ 越大，右边整体越大，坏的泛化发生的可能性就越高。
  • $N$：训练数据的数量。$N$ 越大，指数项 $e^{-2\epsilon^2N}$ 就越小，右边整体越大，坏的泛化发生的可能性就越低。这说明更多的数据有助于提高模型的泛化能力。
  • $\epsilon$：我们容忍的误差范围。 $\epsilon$ 越大，指数项越小，右边越小。这意味着如果我们对训练误差和真实误差之间的差距要求不高，那么坏的泛化发生的可能性就越低。

这个不等式告诉我们，在一定的条件下，我们可以通过控制模型复杂度（假设集大小）和增加数据量来降低坏的泛化发生的风险，从而使我们学到的模型在未知数据上也能有良好的表现。为了让机器学习“可行”，我们需要保证右边的上界足够小。 我们需要：

1. 控制假设集的大小 $M$：不要使用过于复杂的模型，避免假设集过大。
2. 使用足够多的训练数据 $N$：更多的数据能够提供更多的信息，降低坏的泛化发生的概率。

VC Dimension#

我们所看到的霍夫丁不等式形式，主要是针对有限大小的假设集 $\mathcal{H}$ 。在实际的机器学习中，我们经常会遇到无限大小的假设集，例如，二维平面上所有可能的直线，对于这些无限的假设集，我们不能直接使用之前讨论的基于 $M$ 的界限。

为了解决这个问题，我们需要引入VC 维 (Vapnik-Chervonenkis Dimension)，通常记作 $d_{vc}$，是衡量一个假设集复杂程度或者说容量 (capacity) 的一种方式。

对于给定的 $d$ 个数据点，如果一个假设集 $\mathcal{H}$ 能够实现这 $d$ 个数据点的所有 $2^d$ 种可能的二元分类结果，那么我们就说这个假设集能够打散 (Shatter)这 $d$ 个点。例如：在二维平面上，一条直线（我们的假设）可以打散 3 个不在同一条直线上的点。无论这三个点的标签如何组合（正类或负类），我们一般能找到一条直线将它们分开（除了3 个点共线的情况）。但是，一般来说，一条直线无法打散 4 个点。

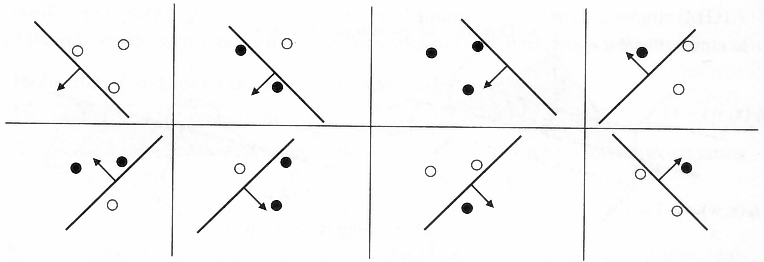
VC dimension $(d_{vc}(\mathcal{H}))$ 就是假设集 $\mathcal{H}$ 能够打散的最多点的数量。即使存在某些 3 个点的排列方式（例如共线）不能被直线打散，只要存在 某些 3 个点的排列方式（例如非共线）可以被直线打散，并且不存在任何 4 个点的排列方式可以被直线打散，那么二维平面上直线的 VC 维就是 3。

VC dimension 的一个核心作用是，即使假设集的大小是无限的，只要它的 VC dimension是有限的，我们仍然可以证明机器学习的可行性。

对于$\mathcal{H} = \lbrace h: \mathcal{X} \to \lbrace+1,-1\rbrace \rbrace$, 我们定义 $h(X_1, X_2,…,X_N)$ 为假设空间 $\mathcal{H}$ 在训练集 $D$ 上的所有对分 (dichotomy)。它表示的是指的是对这 $N$ 个点的所有可能的标签分配方式。例如当 $N=3$ 时且三个点不在一条直线时对分数为8。

为了去掉对具体 $D$ 的依赖性，我们引入了成长函数(growth function)。成长函数 $m_{\mathcal{H}}(N)$ 定义为对于 $N$ 个点，假设集 $\mathcal{H}$ 能够产生的最多不同的对分的数量。对于 $N$ 个点，总共有 $2^N$ 种可能的标签分配方式。

• 如果 $N \le d_{vc}(\mathcal{H})$，那么 $m_{\mathcal{H}}(N) = 2^N$，假设集可以打散这 $N$ 个点。
• 如果 $N > d_{vc}(\mathcal{H})$，那么 $(m_{\mathcal{H}}(N) < 2^N$，假设集无法打散这 $N$ 个点。

对于VC dimension的边界值，我们定义了Break Point (断点) 的概念。在一个假设集 $\mathcal{H}$ 中，break point 指的是最小的整数 $k$，使得对于任意 $k$ 个数据点，$\mathcal{H}$ 都无法打散这 $k$ 个点。如果一个假设集能打散任意 $k-1$ 个点，但不能打散任意 $k$ 个点，那么 $k$ 就是这个假设集的 break point。 在二维空间中，$k=4$。

假设集 $\mathcal{H}$ 的 VC dimension $d_{vc}$ 恰好等于其最小 break point $k$ 减 1，即$d_{vc} = k - 1$。因此，如果一个假设集的 break point 是有限的，那么它的 VC dimensio也是有限的。

最后，我们可以在霍夫丁不等式中，使用 VC dimension 替代$M$：

这个不等式是一种 VC bound (VC界) ，给出了坏的泛化发生的概率的上界。

通过这个式子可以得出：当 $N > d_{vc}$ 时，$m_{\mathcal{H}}(N) \leq N^{d_{vc}}$.

要使得机器学习可行，我们需要这个概率足够小。

• $d_{vc}$ 必须是有限的： 如果 VC dimension 是无限的，那么模型复杂度过高，容易发生过拟合。
• $N$ 必须足够大： 当 $N$ 增大时，指数衰减项 $e^{-\frac{1}{8}\epsilon^2 N}$ 会起主导作用，降低坏的泛化发生的概率。相对于 $d_{vc}$ 来说，我们需要有足够大的 $N$。

总的来说，为了使机器学习模型能够从训练数据中学习到有用的模式并泛化到未见过的数据，我们需要控制模型的复杂度，并且拥有足够多的训练数据。

无论假设集是有限的还是无限的，都要求：

1. $E_{in}(g)$ 足够小： 我们必须能够在训练集上找到一个表现良好的假设 $g$，即训练误差足够小。
2. $E_{out}(g) \approx E_{in}(g)$： 训练误差能够很好地代表泛化误差，这样在训练集上表现良好的假设在未见过的数据上也能表现良好。这通常通过控制模型的复杂度（例如，通过限制假设集的大小或 VC dimension）和使用 足够大 的数据集来实现。

Noise and Error#

以上的Hoeffding’s Inequality 和 VC dimension的应用是在数据集理想的情况下的。但在真实的情况下，经常会存在噪声 (Noise) 和误差 (Error)，它们会不会影响着学习的可行性呢？

在机器学习中，噪声 (Noise) 可以理解为数据中不希望有的、随机的或不正确的成分。这些噪声可能来源于多种途径，例如数据采集过程中的错误，或者目标函数本身固有的随机性

噪声的存在直接影响了我们对误差的衡量。在没有噪声的情况下，我们的目标是找到一个假设$g$，使得它尽可能接近真实的目标函数 $f$。我们通过最小化训练误差 $E_{in}$ 来实现这个目标。然而，当数据中存在噪声时，即使我们找到了在训练数据上表现最好的假设，它也未必是真正接近 $f$ 的假设。

在处理带有噪声的数据时，我们实际上是在处理概率分布。

我们不再假设存在一个确定的目标函数 $f(x)$，而是认为对于每个 $x$，输出 $y$ 是从一个概率分布 $P(y∣x)$ 中抽样得到的.

误差 (Error) 是衡量我们模型的预测与真实值之间差异的指标。在分类问题中，即使存在噪声，我们仍然可以使用 0/1 误差，但在计算期望误差时，需要考虑不同标签出现的概率。于是引入了 $E(g, f)$，可以表达为点误差的平均值。

总的来说：即使存在噪声，Hoeffding 不等式和 VC dimension 在一定程度上仍然适用，只是需要将输出一个固定的值修改为条件概率分布。

我们的学习目标也相应地变为找到一个假设 $g$，使得它在考虑噪声的情况下，尽可能地接近目标分布。

Linear Regression#

我们分析了学习的可能性后，我们知道了如何选择假设集$\mathcal{H}$，以及数据集该怎么设计使得我们的模型泛化能力更好。而演算法 $A$ 则是指导计算机训练数据集的方法。

回归是一种重要的监督学习 (Supervised Learning) 方法，回归的核心目标是找到输入变量（特征）与输出变量（目标）之间的关系，并用数学模型来描述这种关系。它的输出是一个连续的数值型输出，例如，预测房价、预测股票价格、预测用户的年龄等等，都属于回归问题的范畴。

线性回归是最简单的回归模型，它假设输入变量和输出变量之间存在线性关系。

我们通过一个信用卡额度的例子引入。银行在考虑给予不同客户信用卡额度的时候通常会从客户的多种信息综合考察，例如：

在这个例子中，Input Space $x = (x_0,x_1,x_2,...,x_n)$ 可以是不同项目的值，Output Space $y$ 则是预测的信用卡额度，构建这样的映射函数 $h(x)$，在 $y$ 为实数时，我们可以使用加权分数进行计算：$y \approx \sum _{ i = 0 } ^ { d } w _ { i } x _ { i }$

通过这个例子，我们知道了线性回归模型的假设函数（hypothesis）是一个线性函数，可以表示为：$h(x) = w^T x$。

其中，$x$ 是输入特征向量，$w$ 是权重向量。我们的目标就是找到最优的权重向量 $w$，使得模型能够尽可能准确地预测输出值。

在二维空间中，线性回归的目标是找到一条直线，使样本集中的点更接近它。

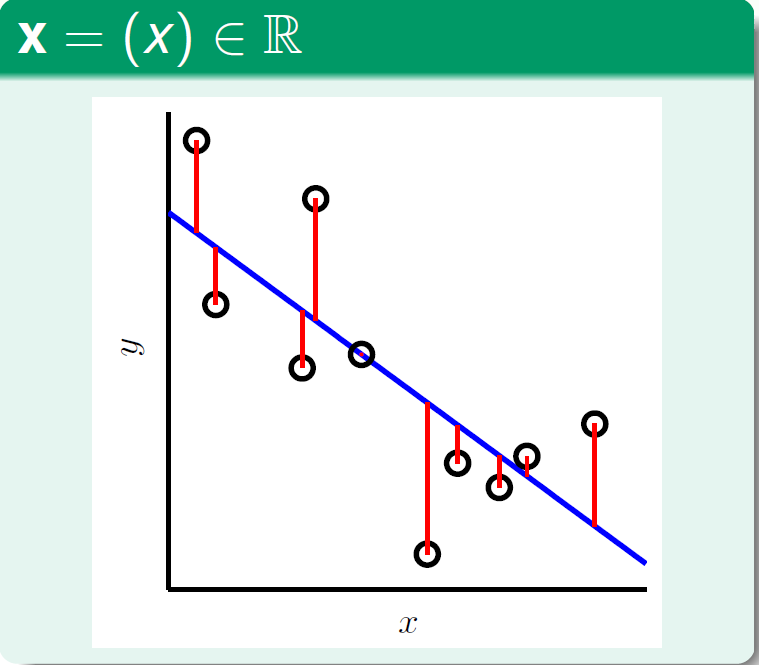
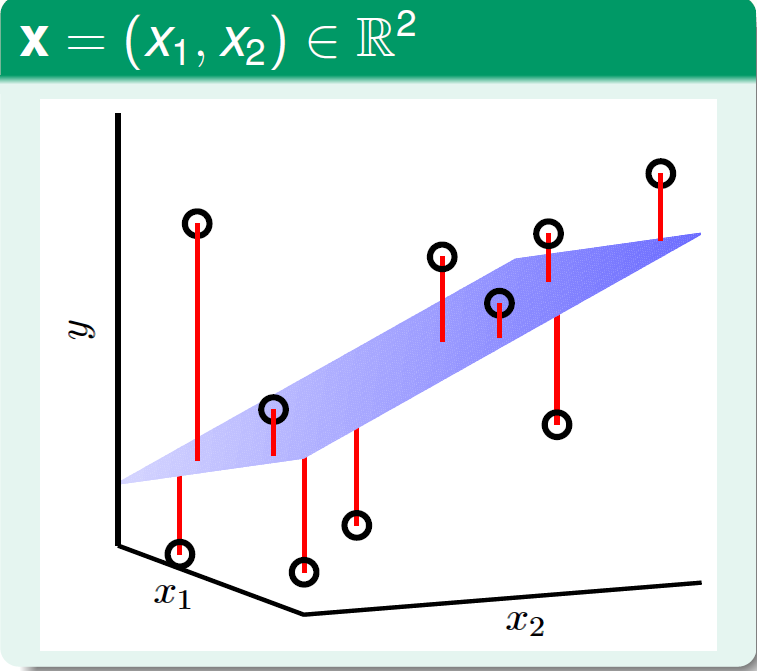
在三维空间中，线性回归的目标则是找到一个平面，使样本集中的点更接近它。

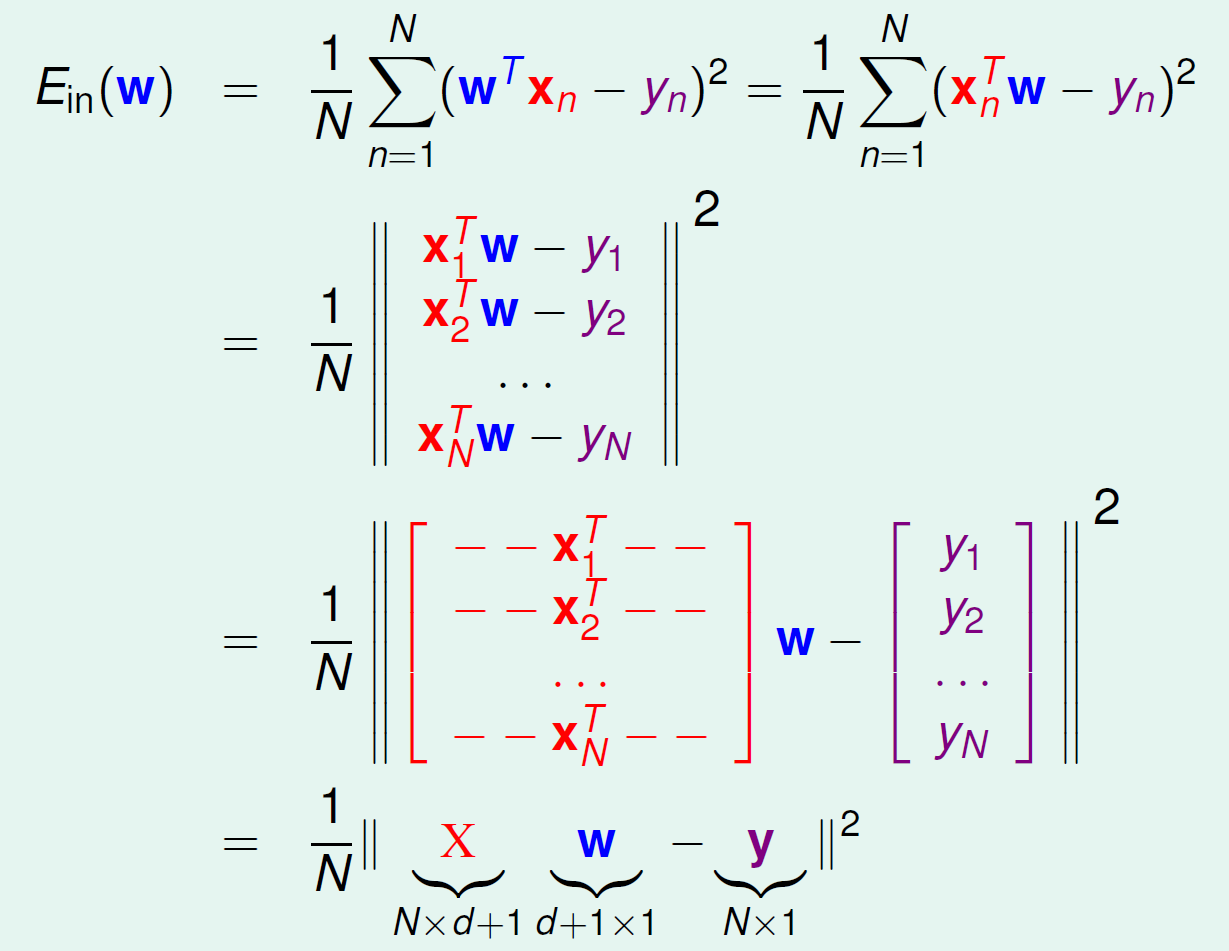
在线性回归中，最常用的衡量预测值与实际值之间差异的方法是平方误差 (Squared Error)。对于一个给定的样本 $(x_n, y_n)$，模型的预测值为 $w^T x_n$，实际值为 $y_n$，则平方误差为 $(w^T x_n - y_n)^2$。

我们的目标是找到一组权重 $w$，使得所有训练样本的平方误差之和最小。这个误差函数被称为均方误差 (Mean Squared Error, MSE) 或平方损失函数 (Squared Loss Function)。根据之前的Hoeffding’s Inequality 和 VC dimension我们知道，若学习是可行的，则$E_{out}(g) \approx E_{in}(g)$。那我们可以使用均方误差推导出线性回归的误差公式：

通过最小化样本数据误差，我们可以找到最佳的模型参数 $w$。

Note: 下面的推导对于概念理解来说可以跳过

我们来根据数学方法化简$E _{ \mathrm { in } } ( \mathbf { w } )$的公式。首先交换$w^Tx_n$为$x_n^Tw$，再根据行列式的知识将$\sum$去掉后化简。

接下来的任务就是化简：$\min_{ w } E _ { i n } ( \mathbf { w } ) = \frac { 1 } { N } \| X \mathbf { w } - \mathbf { y } \| ^ { 2 }$。其中$N$, $X$和$y$都是确定的，而$w$是不确定的。将$w$看成变量，这时变成了一个$w \rightarrow E(w)$的二次函数，$N > 0$，则$w$的系数也大于0，二次函数开口向上，存在一个最小值。根据方差的定义，这个二次函数大致为：

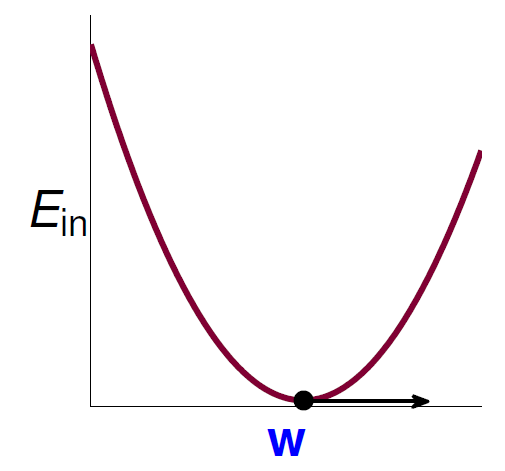
那么，根据二次函数知识，最小值$\mathbf{w}_{LIN}$满足$\nabla E _ { \text {in } }(\mathbf{w}_{LIN}) = 0$。梯度为0的点，即对$w$求导值为0的点为最小值$\mathbf{w}_{LIN}$。

对其$w$求偏导：$\nabla E _ { \text {in } } ( \mathbf { w } ) \equiv \left[ \begin{array} { c } \frac { \partial E _ { \text {in } } } { \partial w _ { 0 } } ( \mathbf { w } ) \\ \frac { \partial E _ { \text {in } } } { \partial w _ { 1 } } ( \mathbf { w } ) \\ \cdots \\ \frac { \partial E _ { \text {in } } } { \partial w _ { d } } ( \mathbf { w } ) \end{array} \right] = \left[ \begin{array} { c } 0\\ 0\\ \cdots\\ 0\\ \end{array} \right]$

对原多项式展开：$E _ { \mathrm { in } } ( \mathbf { w } ) = \frac { 1 } { N } \| \mathrm { Xw } - \mathbf { y } \| ^ { 2 } = \frac { 1 } { N } \left( \mathbf { w } ^ { T } \mathbf { X } ^ { T } \mathbf { X } \mathbf { w } - 2 \mathbf { w } ^ { T } \mathbf { X } ^ { T } \mathbf { y } + \mathbf { y } ^ { T } \mathbf { y } \right)$

对其求导后的结果为：$\nabla E _ { \text {in } } ( \mathbf { w } ) = \frac { 2 } { N } \left( X ^ { T } X \mathbf { w } - X ^ { T } \mathbf { y } \right)$，令其等于0可以得到：$X\mathbf { w } = y$，$\mathbf { w } _ { \mathrm { LIN } } = \mathrm { X } ^ { \dagger } \mathbf { y }$。其中，${ \dagger }$表示伪逆，即将X化简的X矩阵。在$X^TX$可逆时，可以简化为$\mathbf { w } _ { \mathrm { LIN } } = (\mathrm { X }^{T} \mathrm { X })^{-1} \mathrm { X } \mathbf { y }$

总结一下Linear Regression算法的实现步骤：

1. 根据样本数据集，获取输入矩阵（input matrix）和输出向量（output vector）：

2. 计算伪逆(pseudo-inverse)，在可逆的情况下即求逆。

3. 得到最小值$\underbrace{\mathbf { w } _ { \mathrm { LIN } }}_{d+1 \times 1} = \mathrm { X } ^ { \dagger } \mathbf { y }$，此时维度为$(d+1)\times(d+1)$

Logistic Regression#

与线性回归直接预测一个连续的数值不同，逻辑回归（Logistic Regression）预测的是某个事件发生的概率，这个概率值介于 0 和 1 之间3。例如，预测用户是否会点击广告、预测邮件是否为垃圾邮件、预测患者是否患有某种疾病等等。

逻辑回归模型基于线性回归的思想，但对其输出进行了一个转换。首先，我们仍然使用一个线性函数来计算输入特征的加权和，称为线性评分 (linear score)：$s = w^T x$

为了将这个评分值映射到 0 到 1 之间的概率，我们引入了一个Sigmoid 函数（也称为逻辑函数）：$\theta(s) = \frac{1}{1 + e^{-s}}$ 。

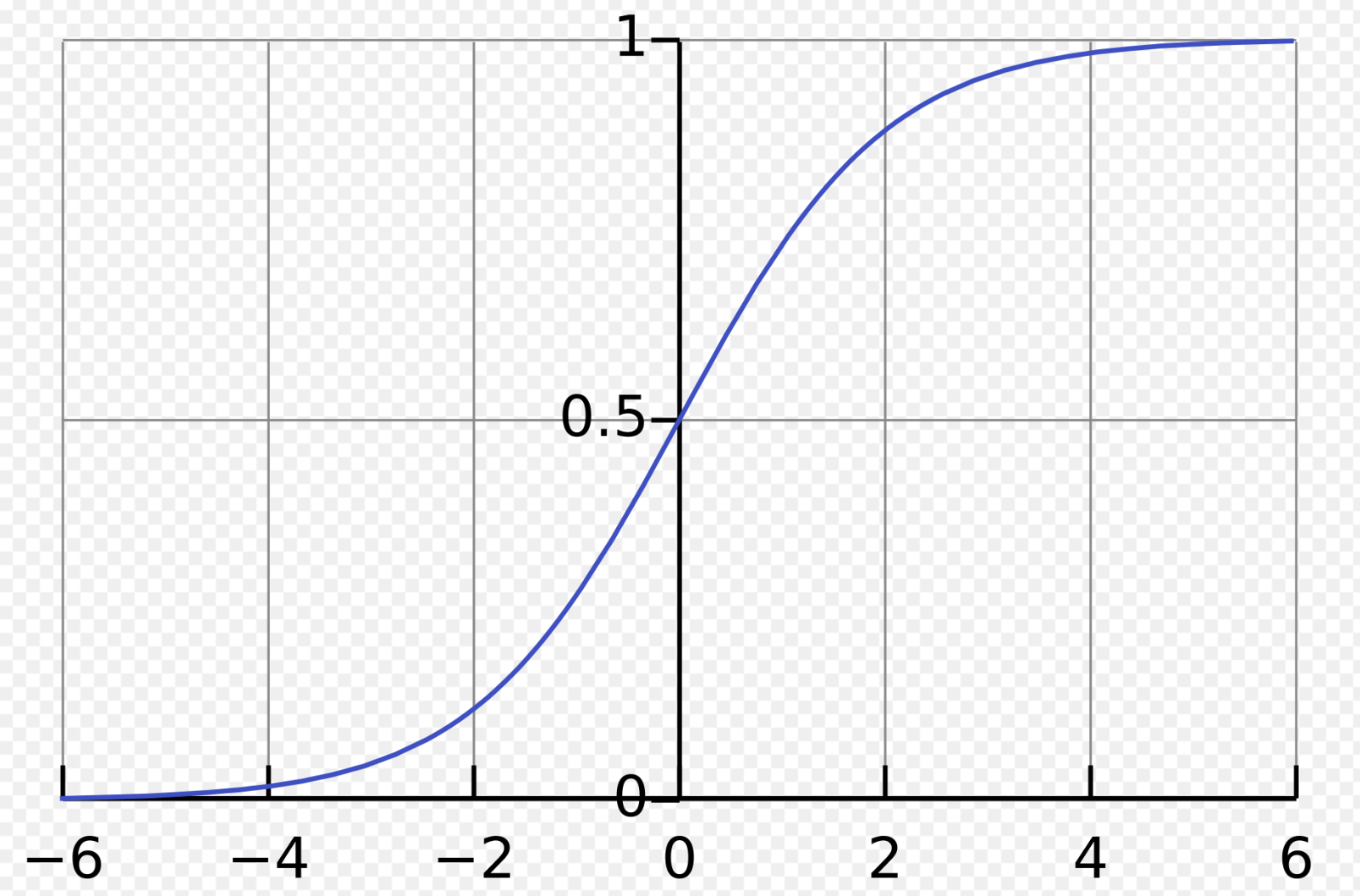
Sigmoid 函数是一个S形的曲线，可以将任意实数映射到 (0, 1) 区间。

因此，逻辑回归的假设函数可以表示为：$h(x) = \theta(w^T x)$ 这个 $h(x)$ 的值就表示样本 $x$ 属于正类（通常标记为 1）的概率。

之前学习的线性回归中，误差是采用方差的形式进行计算的。逻辑回归通常使用交叉熵误差 (Cross-entropy Error) 作为损失函数。对于二元分类问题，交叉熵误差函数的表达式为：

与线性回归不同，逻辑回归的交叉熵误差函数没有闭式解。 我们通常使用梯度下降 (Gradient Descent) 等迭代优化算法来找到使误差函数最小的权重向量 $w$. 梯度下降算法通过不断计算误差函数关于权重的梯度，并沿着梯度的反方向更新权重，逐步逼近最优解。这个过程会在后续的仔细讲解。

Linear Models for Classification#

在前面的学习中，我们已经接触了两种重要的线性模型：线性回归和逻辑回归。我们知道，线性回归最初是用来解决回归问题的，而逻辑回归则专门用于二元分类。 那么，我们是否可以使用线性回归来做分类呢？

我们可以先使用线性回归模型来拟合数据，然后设定一个阈值 (threshold)，根据模型的输出值是否超过这个阈值来判断样本的类别。例如，对于二元分类问题，如果线性回归的输出大于 0，我们就将其归为正类；如果小于 0，就归为负类。

那么此时对于二元分类问题，我们有三种主要的线性模型：

Nonlinear Transformation#

在前面的学习中，我们主要讨论了各种线性模型，包括线性回归、逻辑回归以及使用 PLA 的线性分类器。 这些模型在处理线性可分的数据时表现良好。

那么，当数据不是线性可分时，我们该如何使用线性模型呢？ 非线性变换(Nonlinear Transformation) 提供了一种巧妙的解决方案.

假设我们有一些一维的数据点，我们想要用一个二次曲线来进行分类。原始的特征空间是一维的，我们无法用一条直线将数据分开。但是，我们可以将每个一维的数据点 $x$ 变换到一个二维空间，例如使用变换 $\Phi(x) = (x, x^2)$。

这样，原始数据点在一维空间中无法线性分割，但在新的二维空间中，我们就可以使用一条直线来分割变换后的数据点。

非线性变换的核心是将原始数据通过一个非线性函数 $Φ$ 映射到更高维度的空间。

1. 变换原始数据 (Transform original data)： 对于原始数据集 $\{(x_n, y_n)\}$, 我们使用非线性变换 $\Phi$ 将每个数据点 $x_n$ 映射到新的表示 $z_n = \Phi(x_n)$。这样，我们就得到了新的数据集 $\{(z_n, y_n)\}$，其中特征已经过非线性变换。

2. 在变换后的数据上训练线性模型 (Get a good perceptron using the transformed data)： 在变换后的数据集 $\{(z_n, y_n)\}$ 上，我们使用我们熟悉的线性分类算法 $A$，例如PLA，来学习一个好的线性模型。这个线性模型在变换后的空间中找到一个权重向量 $\tilde{w}$。

3. 返回最终的假设 (Return the final hypothesis)： 最终得到的分类模型 $g(x)$ 是在原始输入 $x$ 上应用的，其形式为 $g(x) = \text{sign}(\tilde{w}^T \Phi(x))$。 这意味着，虽然我们在变换后的空间中学习了一个线性的决策边界，但当应用到原始输入时，由于 $\Phi(x)$ 的存在，它实际上是一个非线性的决策边界。

模型的学习过程发生在变换后的空间中，但最终的预测模型作用于原始输入数据经过变换后的表示。

Overfitting#

模型的能力越强，就越容易出现一个问题，那就是过拟合 (Overfitting)。过拟合指的是模型在训练数据上表现得非常好，但在新的、未见过的数据上表现得很差的现象。 就好像一个学生只记住了课本上的答案，而没有真正理解知识，一旦考试题目稍有变化就束手无策。(别看了，说的就是你🥹)

Overfitting的出现原因可能有：

1. 模型过于复杂 (Model Complexity)：当我们使用非常复杂的模型，例如高阶多项式变换，模型拥有了很强的“记忆”能力，它可以记住训练数据中的每一个细节，包括一些噪声或者偶然的模式。 例如在 VC Bound 中，模型复杂度过高会使得$d_{vc}$趋向于无限大，导致泛化误差的上限增大。
2. 训练数据不足 (Limited Data)：如果训练数据的量不够大，模型很容易记住这些有限的样本，而无法学习到数据背后真实的分布规律。这就好比只给了学生几道例题，他就以为掌握了所有题型。(这还是你🤣)
3. 数据中存在噪声 (Noise in the Data)：真实世界的数据往往包含各种各样的噪声。过拟合的模型不仅学习了数据中的真实信号，也学习了这些噪声，导致在新数据上的表现不佳。

这是一个因为模型过于复杂造成的Overfitting的例子：假设真实的目标函数是一个二次多项式，但我们使用了一个四次多项式模型进行拟合。即使训练数据带有少量噪声，四次多项式也可能完美地拟合训练数据中的每一个点，包括那些由噪声引起的波动。然而，这样的模型并不能很好地预测新数据。

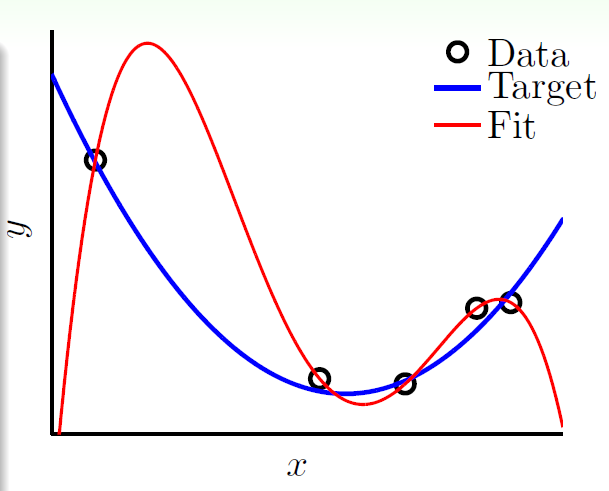
根据VC Bound理论，阶数越大，即VC Dimension越大，泛化误差($E_{out}$) 很高。此时 训练误差 ($E_{in}$) 很低，因为在训练数据上拟合得很好。

这就是过拟合的典型特征：$E_{in}$很小，$E_{out}$却很大。

过拟合的发生还与数据中的噪声密切相关。这里的噪声可以分为两种：

• 随机噪声 (Stochastic Noise, $\sigma ^2$)：这是由数据标记错误或者数据本身固有的随机性造成的。

• 确定性噪声 (Deterministic Noise)：这是由于我们选择的假设空间 $\mathcal{H}$ 无法完美地表示目标函数 $f(x)$ 而产生的。即使数据没有随机噪声，只要我们的模型不够复杂到能够完全拟合 $f(x)$，就会存在确定性噪声。

例如下面这个例子。当模型很复杂的时候，即50阶多项式的目标函数，无论是2阶模型还是10阶模型，都不能学习的很好。即使训练数据中没有随机噪声，如果目标函数本身就很复杂，而我们使用的模型又相对简单，那么模型仍然无法完美拟合数据，这也会导致类似过拟合的现象。

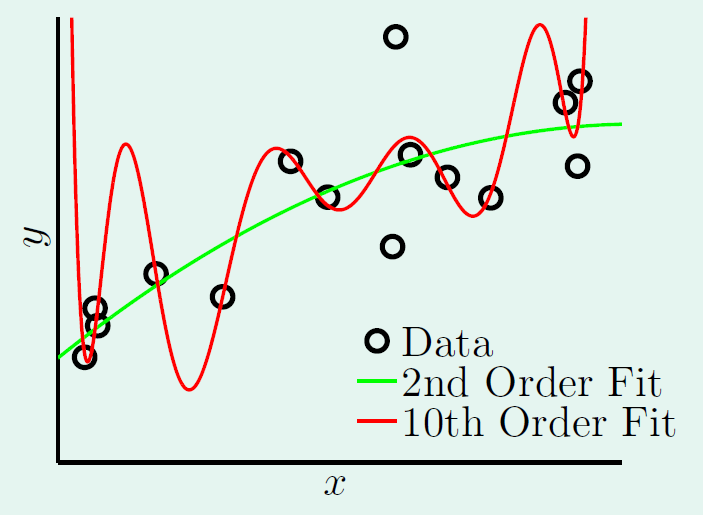
当然，过拟合还与训练数据的规模有关，如果训练的数据越少，越容易出现过拟合的问题，正如我们在前面解释模型过于复杂的时候的例子，只有5个数据的情况下会导致假设与目标函数误差增大。

总结一下，有四个因素会导致发生Overfitting：

1. 训练集大小(Dataset Size) $N$：过小
2. 随机误差(Stochastic Noise) $\sigma ^2$: 过大
3. 确定性误差(Deterministic Noise) $Q_f$: 过大
4. 模型能力(Excessive Power)：过强

这里会在后续的章节中详细说明。

以下是几种常见的应对过拟合的方法：正则化 (Regularization)和数据验证 (Validation)，在后面的内容中提到。

Regularization#

正则化 (Regularization) 的一个核心思想是限制模型的复杂度，从而避免模型过于“自由”地拟合训练数据中的噪声。

一种正则化的方法是Regularized Fit. 它是从一个非常强大的假设集合（例如 $H_{10}$，代表高阶多项式）“退一步”到一个更简单的假设集合（例如 $H_2$，代表低阶多项式）虽然我们仍然在大的假设空间中搜索，但正则化的惩罚项会引导我们倾向于选择复杂度较低的模型。

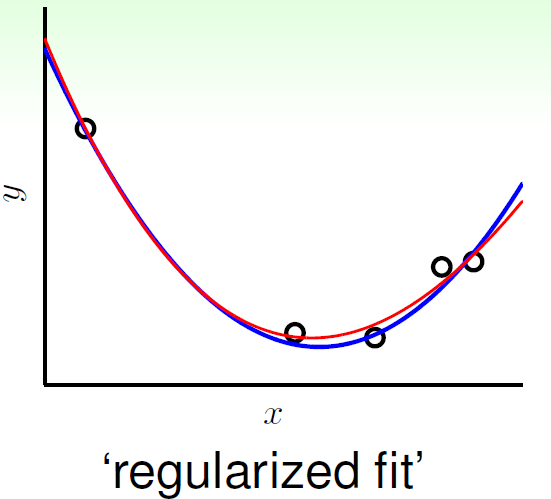
$H_{10}$的表达式可能是：$H_{10}=w_0+w_1x+w_2x^2+w_3x^3+\cdots+w_{10}x^{10}$

$H_2$则可以表示为：$H_2=w_0+w_1x+w_2x^2$

所以，如果限定条件是$w_3 = w_4 = ... = w_{10} = 0$，那么就有$H_2 = H_{10}$。我们可以将其高阶部分的权重w限制为0，相当于从高阶的形式转换为低阶，fit波形更加平滑，不容易发生过拟合。

我们使用$w_{REG}$ 代表在使用正则化方法后，通过最小化增强的误差函数所得到的最佳权重向量。简单来说，当我们使用正则化时，我们不再仅仅关注在训练数据上的表现（即最小化 $E_{in}$），而是希望找到一个在训练数据上表现良好，同时模型复杂度又不会太高的权重向量。$w_{REG}$ 就是在这个权衡下找到的最优解。

L2 正则化，也称为岭回归 (Ridge Regression) 或权重衰减 (Weight Decay)，是一种常用的正则化方法。它的核心思想是在损失函数中加入模型权重的平方和，从而限制模型参数的大小，防止过拟合。

假设我们有一个原始的损失函数 $E_{in}(w)$，L2 正则化项是所有模型权重 $w_j$ 的平方和，并乘以一个正则化系数 $\lambda$得到：$\frac{\lambda}{N} \sum_{j=1}^{n} w_j^2$。其中，$N$ 是样本数量，$\lambda$ 是控制正则化强度的超参数。

将 L2 正则化项加入到原始损失函数中，得到增强的误差 $E_{aug}(w)$： $E_{aug}(w) = E_{in}(w) + \frac{\lambda}{N} \sum_{j=1}^{n} w_j^2$

我们的目标是最小化 $E_{aug}(w)$，得到最佳权重向量 $w_{REG}$，这样，模型在训练过程中不仅要拟合训练数据，还要尽可能减小权重的值，从而降低模型复杂度。

增强的误差 (Augmented Error) $E_{aug}(w)$ 是在原始训练误差 $E_{in}(w)$ 的基础上，加入了正则化项后得到的新的误差函数。增强的误差本质上是在训练误差的基础上，对模型的复杂度进行了惩罚。

正则化通过限制权重的幅度，实际上是降低了模型的有效复杂度，从而降低了模型的 VC dimension，提高了模型的泛化能力。

除了 L2 正则化，还有其他类型的正则化方法，例如 L1 正则化，它使用权重向量的 L1 范数 $\|w\|_1$ 作为惩罚项。L1 正则化倾向于产生稀疏的权重向量，即许多权重为零，可以起到特征选择的作用。这是它的增强误差：

• 对于 L1 正则化： $E_{aug}(w) = E_{in}(w) + \frac{\lambda}{N} \sum_{j=1}^{n} |w_j|$
• 对于一般的正则化： $E_{aug}(w) = E_{in}(w) + \frac{\lambda}{N} \Omega(w)$ 其中，$\Omega(w)$ 是正则化项，可以是 L1、L2 或其他形式。

在实际应用中，我们通常使用梯度下降法来最小化 $E_{aug}(w)$。

此外，正则化参数 $\lambda$ 的选择至关重要。如果 $\lambda$ 太小，则正则化效果不明显，仍然可能发生过拟合；如果 $\lambda$ 太大，则可能导致模型欠拟合。如何选择合适的 $\lambda$ 需要使用验证 (Validation) 等技术。

Validation#

我们了解了过拟合的风险以及如何使用正则化来降低这种风险。但是，当我们有多种模型选择，例如不同的算法、不同的正则化参数 $\lambda$，或者不同的特征转换方式时，我们如何选择最佳的模型呢？这就是 验证 (Validation) 要解决的问题。

仅仅是二元分类问题，我们学习到非常多的模型，有PLA, 线性回归, 逻辑回归等。我们不能简单地使用训练误差 $E_{in}$ 来选择模型，因为这样做会倾向于选择在训练数据上表现最好的模型，而这往往是复杂度最高的模型，容易导致过拟合。

为了解决这个问题，我们引入了验证集 (Validation Set) 的概念。验证集是从训练数据中划分出来的一部分数据，用于模拟模型在未知数据上的表现。 通常，我们会将原始的训练数据分成三个部分：

1. 训练集 (Training Set)：用于训练模型的参数。
2. 验证集 (Validation Set)：用于选择模型（例如选择合适的超参数）。
3. 测试集 (Test Set)：用于最终评估模型的泛化能力。

验证的过程通常包括以下几个步骤：

1. 在不同的模型设置下进行训练：使用训练集训练多个不同的模型，这些模型可能具有不同的算法、超参数或结构。
2. 在验证集上评估性能：使用验证集评估每个模型的性能，计算其验证误差 $E_{val}$。
3. 选择最佳模型：选择在验证集上表现最佳（即 $E_{val}$ 最小）的模型。
4. 最终训练（可选）：使用全部的训练数据（包括最初的训练集和验证集）重新训练选定的最佳模型。
5. 在测试集上进行最终评估：使用测试集评估最终模型的泛化能力。

我们有很多的验证方法，其中 留一法交叉验证 (Leave-One-Out Cross Validation, LOOCV) 提供了几乎无偏的估计，但计算成本高昂，而 V 折交叉验证 (V-Fold Cross Validation) 则是一种更实用的方法，它可以在计算成本和性能之间取得较好的平衡。

Three Learning Principles#

在机器学习中，我们有三大学习原则，可以帮助我们更好地理解和应用各种学习算法。

1. 奥卡姆剃刀 (Occam’s Razor)：在所有可能解释数据的模型中，我们应该选择最简单的那个。简单模型通常泛化能力更强，不容易过拟合。

   举个简单的例子，假设你早上出门，看到地是湿的。可能有两种解释：

   • 解释一：昨晚下雨了。
   • 解释二：有人在半夜偷偷给你家门口洒水了，然后又偷偷把洒水工具收走了，而且没有人看到。

   虽然两种解释都可能成立，但是解释一明显更简单，只需要一个假设（下雨了）。解释二则有很多额外的假设，比如有人偷偷洒水、偷偷收工具等等。按照奥卡姆剃刀原则，我们应该选择解释一。

2. 采样偏差 (Sampling Bias)：这个原则强调训练数据和测试数据必须来自相同的分布。如果训练数据不能代表真实的应用场景，那么学习到的模型在实际应用中表现就会很差。 如果你想知道全班同学的平均身高。如果你只测量了篮球队队员的身高，然后用这个平均值来代表全班的平均身高，那肯定是不准确的，因为篮球队员的身高普遍比其他同学高。这就是一个“采样偏差”的例子。你选择的样本（篮球队员）并不能很好地代表整个群体（全班同学）

3. 数据窥探 (Data Snooping)：这个原则告诫我们在模型选择和训练过程中，要避免“偷看”测试数据。如果我们在模型开发的过程中使用了测试数据的信息，那么最终得到的模型在真实的未知数据上的表现可能会被高估。 “数据窥探”就像考试作弊一样。假设你在参加一个考试，考试前偷偷看到了答案，然后根据答案来复习和准备，这样你在考试中取得好成绩就不能真实反映你的学习水平了。

Neural Network#

神经网络 (Neural Network) 是一种受人脑神经系统启发而设计的计算模型。它由多个相互连接的节点（称为“神经元”）组成，这些节点按层级排列，形成一个网络结构。每个神经元接收来自其他神经元的输入，进行加权求和，并通过一个激活函数产生输出。

一个典型的神经网络由以下部分组成：

• 输入层（Input Layer）：接收外部数据，每个节点对应一个输入特征。$x_0, x_1, x_2, ..., x_d$
• 隐藏层（Hidden Layer）：位于输入层和输出层之间，负责数据的特征提取和非线性变换。包含多个神经元，对输入进行非线性的变换和特征提取。一个隐藏层中的每个神经元都接收前一层所有神经元的输出作为输入，并应用一个激活函数 (activation function) 进行处理。常用的激活函数包括 $\tanh$、sigmoid 和 ReLU 等。
• 输出层（Output Layer）：产生最终的输出结果。

每个节点（神经元）接收来自上一层节点的输入信号，这些输入信号与对应的 权重（Weight） 相乘后求和，再通过一个 激活函数（Activation Function） 进行非线性变换，得到输出信号。

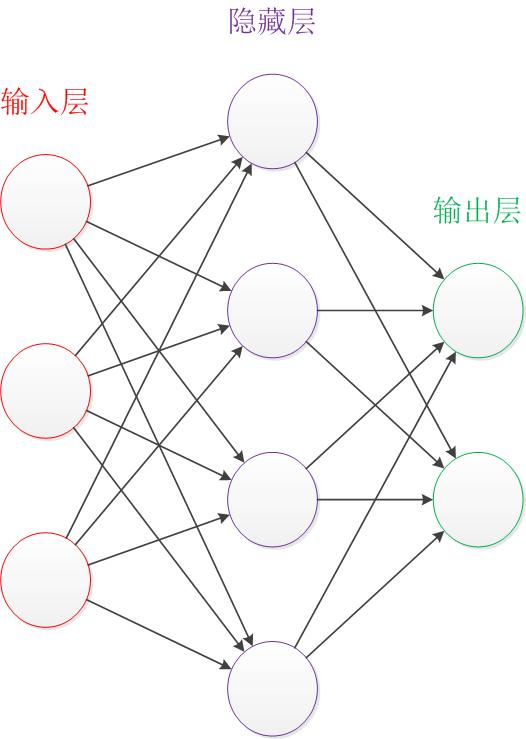
信息在网络中从输入层向输出层单向传递，这个过程称为前向传播 (forward propagation)。数据从输入层开始，逐层传递到隐藏层和输出层。在每个节点，计算加权输入之和，然后通过激活函数得到输出。

我们之前学过的感知机模型 (Perceptron) 其实就是一种单层的神经网络，它的公式是：

在感知机中，有两个层次。分别是输入层和输出层。输入层里的“输入单元”只负责传输数据，不做计算。输出层里的“输出单元”则需要对前面一层的输入进行计算。

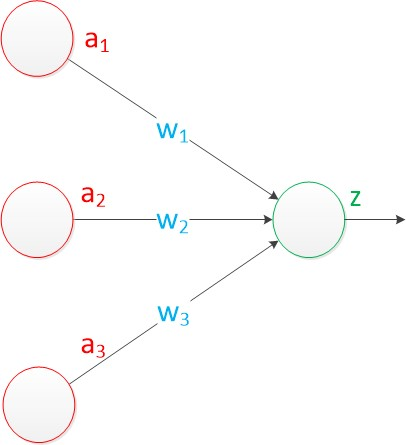
如果我们在感知机模型的基础中，加入一层隐藏层单层感知器神经网络，那么单个感知机模型就变成了多个感知机的线性组合，我们把它称为单层感知器神经网络 (Single Perceptrons Neural Network)。

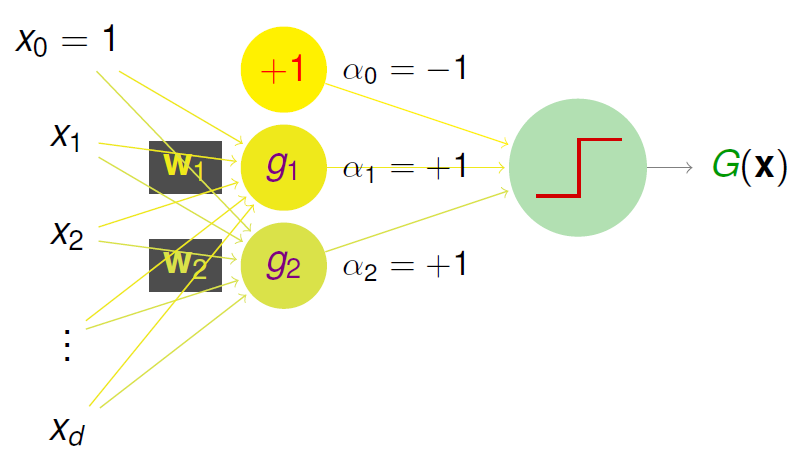
上面这个模型包含了两层的权重，分别是$w_t$和$\alpha_t$。这个模型首先将左边的输入$(x_1, x_2, ..., x_d)$与不同的权重$(w_1,w_2,...,w_t)$相乘，得到$T$个不同的感知机$(g_1,g_2,...,g_T)$。最后，每个感知机再给予不同的权重$(\alpha_1,\alpha_2,...,\alpha_t)$，通过线性组合得到$G(x)$。那么我们把这样的组合感知机公式写成：

其中的 $sign(w_t^T\mathbf{x})$ 就是第一层的感知机 $g_t(\mathbf{x})$。通过这样的模型我们可以实现一些简单的边界划分问题，例如：

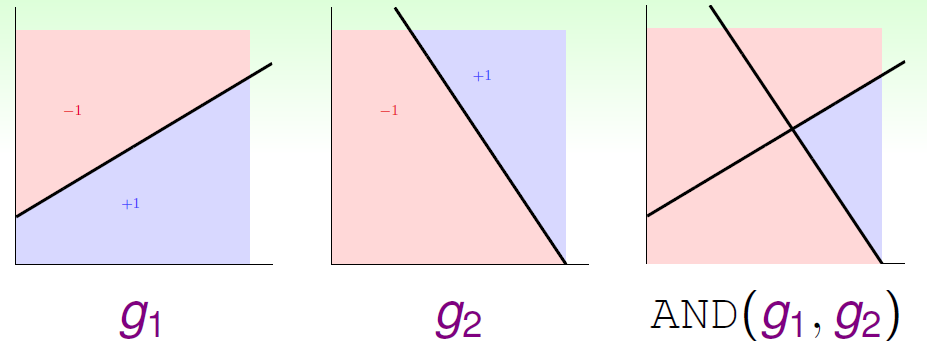
但是，单层感知器神经网络能力再强也是有限的，有些逻辑也无法完成。比如，XOR异或运算。这个时候就需要多层感知机神经网络 (Multi-Layer Perceptrons Neural Network) 了。例如，XOR异或可以等价于：

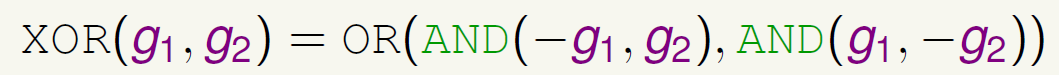
那我们可以设计如下的多层感知机神经网络：

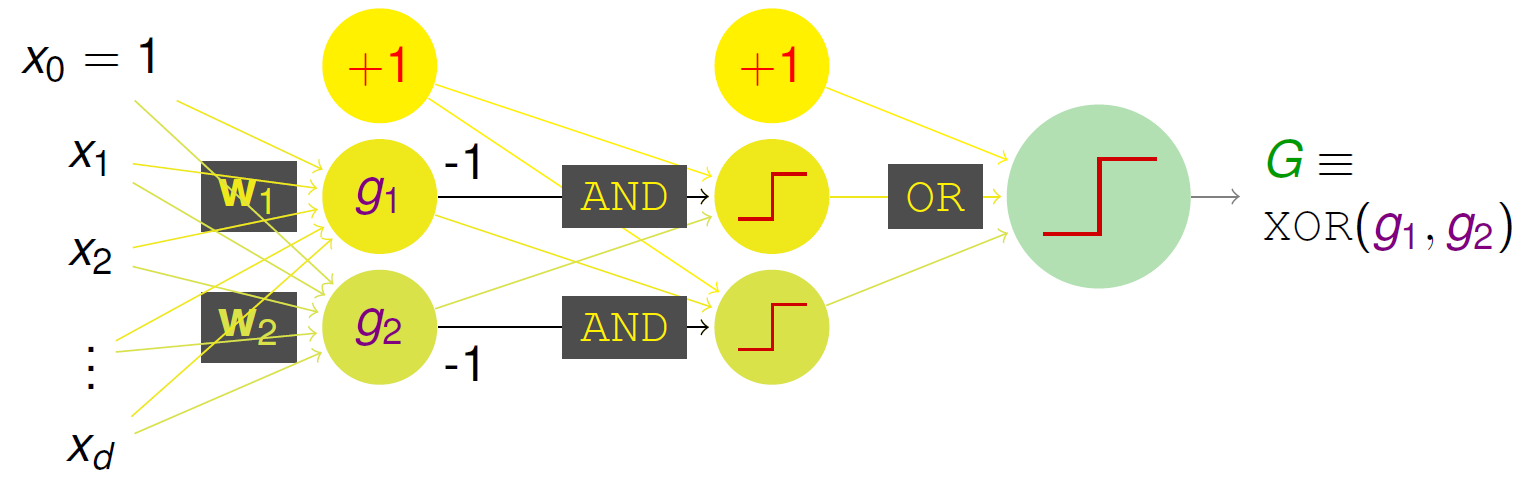
我们发现隐藏层1到隐藏层2之间经历了一个AND操作变化，而隐藏层2到输出层之间经历了一个OR操作变化。我们习惯将这些对当前层的输入数据进行转换的操作称为变换(Transform)。上面例子中存在两个Transform。

那我们的神经网络的过程可以总结为：输入层输入各种特征参数数据，经过隐藏层的一层层运算，即Transform，在输出层得到一个分数$s$，再根据具体问题使用不同的激活函数进行非线性变换得到目标输出。 在感知机模型中，我们的激活函数就是 $sign()$ 函数，它把我们的结果分类到正类和负类上。

常用的激活函数包括：

• Sigmoid 函数：将输入映射到 $(0,1)$ 区间，公式为：

  $$\sigma(z) = \frac{1}{1 + e^{-z}}$$

• Tanh 函数：输出范围为 $(-1,1)$，公式为：

  $$\tanh(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}}$$

• ReLU 函数：修正线性单元，公式为：

  $$\text{ReLU}(z) = \max(0, z)$$

我们知道了神经网络的基本结构后，我们知道对于每一层计算，都有不同的权重参数$w^{(l)}_{ij}$。$i$表示输入层神经元的编号，而$j$表示处理层神经元的编号，$l$表示处理层的层级编号。

要确定整个神经网络的结构，其实就是确定各层的权重参数$w^{(l)}_{ij}$。神经网络的学习目标是找到合适的权重 $\{w^{(\ell)}_{ij}\}$，使得模型在训练数据上的误差 $E_{in}$ 最小化。

那么如何根据已有的样本数据，找到最佳的权重，并使得error的计算最小化呢？这就需要使用反向传播 (Backpropagation) 算法了。

反向传播（Backpropagation）是一种高效计算误差函数关于每个权重的梯度的方法。 分为以下几个步骤：

1. 前向传播 (Forward Propagation)：将输入数据从输入层传递到输出层，计算出网络的预测结果。
2. 计算误差：从输出层开始，计算每个节点对误差的贡献，逐层向前传递。
3. 更新权重：根据误差和学习率，调整各连接的权重，使模型逐步收敛，误差减少。

反向传播算法的过程将会在之后的章节中深入讲解。

Deep Learning#

深度学习 (Deep Learning) 可以看作是具有多个隐藏层的神经网络，相较于传统的浅层神经网络，深度神经网络通过增加层数，能够自动学习数据的多层次特征表示，对复杂的模式和高维数据具有强大的建模能力。

在深度神经网络中，每一层都可以被视为对前一层输出的进一步抽象和特征提取。通过逐层提取特征，网络能够从原始输入中学习到更加抽象、高级的表示。这种逐层抽象的过程，使得深度神经网络在处理诸如图像、语音和自然语言等复杂数据时具有显著优势。

深度学习在实际应用中面临以下主要挑战：

1. 困难的结构设计：确定网络的层数、每层的神经元数量以及连接方式，需要大量的经验和试错。可以利用领域知识和先验经验来设计网络结构。
2. 模型复杂度高：深度网络具有大量的参数，容易发生过拟合。需要大量的数据进行训练，或者采用正则化技术来防止过拟合，如 Dropout 和 权重衰减。
3. 优化困难：深度网络的训练可能会遇到梯度消失或梯度爆炸问题，导致模型难以训练。使用合适的激活函数（如 ReLU），以及采用更先进的优化算法（如 Adam、RMSProp）来改进训练过程。
4. 计算资源需求大：训练深度网络需要大量的计算资源和时间。可以利用 GPU 加速计算，或者使用分布式计算等技术。

为了应对以上挑战，深度学习中发展了多种关键技术。

1. 预训练（Pre-training）预训练是指在正式训练前，对网络进行初始化，以避免陷入不良的局部最小值。常用的预训练方法包括 自编码器（Autoencoder） 和 逐层预训练，通过无监督学习来初始化每一层的权重。

2. 正则化（Regularization）

• Dropout：在训练过程中，随机“丢弃”部分神经元，防止神经元间的共同适应，降低过拟合风险。
• 去噪自编码器（Denoising Autoencoder）：在输入中添加噪声，训练模型去重构原始未受扰动的输入，从而增强模型的鲁棒性。

在之后的章节中，将深入理解Dropout的方法用于降低过拟合的风险。

Error Parameters and VC Dimension#

在机器学习中，我们通常会遇到以下几种误差：

• $E_{in}$ (In-sample Error)：也称为 训练误差 (Training Error) 或 经验误差 (Empirical Error)，指的是你的模型在训练数据集上的表现，它衡量的是模型在已知的训练样本上预测错误的比例。

• $E_{out}$ (Out-of-sample Error)：也称为 泛化误差 (Generalization Error)，指的是你的模型在未见过的、新的数据集上的表现。这才是我们真正关心的误差，因为它反映了模型在实际应用中的预测能力。机器学习的最终目标是使 $E_{out}$ 尽可能地小。

• $E_{model}$ (Model Complexity)：并不是一个可以直接计算的误差值，而是一个用来描述 模型复杂度 (Model Complexity) 的概念。一个模型的复杂度可以理解为它拟合各种不同数据模式的能力。更复杂的模型通常具有更强的拟合能力，但也更容易过拟合。

当我们只关注降低 $E_{\text{in}}$ 时，模型往往会“过拟合（overfitting）”——在训练集上表现极好，但在测试集（即对真实分布的新数据）上表现不佳。这就带出了模型容量（capacity）或者说复杂度的问题：一个模型若“可表达的函数/假设集合”越大，往往越能在训练集中获得极低的误差，但也就越容易记住噪声，从而导致 $E_{\text{out}}$ 可能不理想。

VC Dimension（VC 维度） 就是用来衡量一类模型（假设空间）能实现的最大区分能力（或可塑能力）的一个指标。模型越复杂，VC 维度越高，越容易过拟合，但也有更多的潜力来拟合真实分布。

对于一个给定的假设集合 $\mathcal{H}$，它的 VC Dimension 是指：能找到 $d$ 个点，使得这 $d$ 个点在 $\mathcal{H}$ 的作用下可以产生所有 $2^d$ 种可能的二元标记（即所有正负标签组合），并且没有比 $d$ 更大的数可以满足这个条件。

例如二维平面上的“线性分类”，一条直线（线性分类器）的 VC 维是 3。这意味着存在 3 个点，无论这 3 个点如何标记为正类或负类，我们总能找到一条直线将它们完美分开。但是，对于任意 4 个点，可能存在一种标记方式，使得无法用一条直线将它们分开。

最简单的理解：VC Dimension 是最少能摆出多少个点，让某一类模型对它们的任意标记都能找得到对应的分类函数。

机器学习的核心目标是让模型在未知数据上的表现良好，我们需要确保 $E_{in}$ 能够有效地代表 $E_{out}$。

通过Hoeffding’s Inequality，我们可以知道$E_{in}$ 和 $E_{out}$ 之间差异的概率上界与假设集的大小 $M$ 和 训练数据的数量 $N$ 有关：

然而，在实际的机器学习问题中，我们经常会遇到无限大的假设集。当 $M$ 是无限大的时候，霍夫丁不等式中的 $2M$ 项也会变成无穷大，导致不等式失去意义，无法提供有用的界限。VC Dimension 提供了一种衡量假设集复杂度的替代方法，即使当假设集的大小 $M$ 是无限的时候，VC 维仍然可以是有限的。

VC Bound 给出了一个泛化误差的上限，它告诉我们当训练数据足够多时，且假设集的 VC 维有限时，$E_{in}$ 能够很好地估计 $E_{out}$。

理想情况下，我们希望找到一个合适的VC Dimension，使得模型既能很好地拟合训练数据，又能具有良好的泛化能力。太小的VC Dimension会导致欠拟合，而太大的VC Dimension则会导致过拟合。

在实际学习中，我们经常使用学习曲线去可视化训练过程中的 $E_{in}$ 和 $E_{out}$ 的变化。学习曲线 (learning curve) 是一种可视化工具，用于展示机器学习模型在训练过程中性能如何随着训练数据集大小的变化而变化

通常，学习曲线会绘制两条线：

1. 训练误差曲线 (Training Error Curve)：显示模型在训练集上的误差随着训练样本数量增加而变化的趋势。实际上就是随着训练数据量 $N$ 的变化，$E_{in}$ 的变化情况，随着训练数据量的增加，模型在训练集上见过的样本越来越多，因此训练误差会逐渐降低。
2. 验证误差曲线 (Validation Error Curve) 或 测试误差曲线 (Test Error Curve)：显示模型在验证集或测试集上的误差随着训练样本数量增加而变化的趋势。可以用来近似地观察 $E_{out}$ 随着训练数据量 $N$ 的变化情况。一般来说，随着训练数据量的增加，模型学到的规律更加普适，因此验证/测试误差会先降低，然后趋于稳定。

学习曲线的横轴通常是训练样本的数量，纵轴是误差值（例如，分类错误率、均方误差等）。

Overfitting and Solution#

过拟合 (overfitting) 指的是模型在训练数据上表现得非常好，但在未见过的、新的数据上表现却很差的现象。 当发生过拟合时，我们会观察到 $E_{in}$ 很低，而 $E_{out}$ 很高。这表明模型记住的是训练数据，而不是学习到一般的潜在模式。

过拟合的产生通常有以下几个主要原因：

1. 数据量 N (data size N): 当数据量 N 较小时，更容易发生过拟合。 当训练数据量 N 很小时，模型很容易“记住”训练数据中的每一个样本，包括一些偶然出现的、不具有代表性的样本。模型会过度关注训练数据中的细节，而无法学习到能够泛化到新数据的通用规律。
2. 随机噪声 (stochastic noise): 当随机噪声增大时，过拟合的风险增大。随机噪声指的是数据中固有的、无法避免的随机误差或不确定性。如果模型过于复杂，它可能会将这些随机噪声也学习进去，导致在新的、没有这些噪声的数据上表现不佳。
3. 确定性噪声 (deterministic noise): 当确定性噪声较大时，过拟合的风险也较高。 确定性噪声指的是由于我们选择的假设集 $\mathcal{H}$ 的局限性，导致无法完美表示真实的目标函数 $f$ 而产生的误差。例如真实的目标函数 $f$ 是一个非常复杂的曲线，而我们选择的假设集 $\mathcal{H}$ 是一些简单的直线。 无论我们如何调整直线的参数，都无法完美地拟合这个复杂的曲线。 确定性噪声 就是指用 $\mathcal{H}$ 中最好的模型 $h^*$ 去逼近 $f$ 时，两者之间的差异。
4. 模型复杂度 (Excessive Power): 模型复杂度过高是导致过拟合的重要原因。我们在之前的学习中可以知道：模型的复杂度通常使用 VC Dimension ($d_{vc}$) 表示，VC Dimension 越高，模型能够拟合的函数就越复杂。

有两种常见的解决过拟合问题的方法：正则化 (Regularization) 和使用 训练集-验证集-测试集 (Training-Validation-Test Dataset)

1. 正则化 (Regularization): 正则化是一种在模型训练过程中，通过添加一些额外的约束或惩罚项，来限制模型复杂度的技术。它的目的是防止模型过于“自由”地拟合训练数据中的噪声。 一个常见的正则化方法是 L2 正则化 或 L1 正则化

   • L2 正则化，也称为岭回归 (Ridge Regression) 或权重衰减 (Weight Decay)，是一种常用的正则化方法。它的核心思想是在损失函数中加入模型权重的平方和，从而限制模型参数的大小，防止过拟合。如果模型的权重越大，惩罚就越大，模型就会倾向于选择权重较小的参数，从而使模型更加简单，VC Dimension下降。
   • L1 正则化：将系数的绝对值加入到损失函数中，导致一些系数变为零，从而生成稀疏模型。

2. 训练集-验证集-测试集 (Training-Validation-Test Dataset): 在实际应用中，我们通常会将数据集分成三个部分：

   • 训练集 (Training Set)： 用于训练模型的参数。
   • 验证集 (Validation Set)： 用于在训练过程中评估模型的性能，并帮助我们选择合适的模型（例如，调整正则化参数、选择不同的模型结构等），防止在训练集上过拟合。
   • 测试集 (Test Set)： 用于在模型训练完成后，对模型的最终性能进行评估。 测试集在整个训练过程中是“不可见”的。

   通过使用验证集，我们可以监控模型在未见过的数据上的表现，如果在验证集上的性能开始下降，就可能意味着模型开始过拟合训练集，这时我们可以提前停止训练或者调整模型参数。

Backpropagation Algorithm and Optimize Neural Network#

在机器学习中，假设 (Hypothesis) 就是我们想要学习的函数模型，对于神经网络来说，它的假设是一个非常复杂的、非线性的函数，通过多层相互连接的神经元（也称为节点）构成。

可以把一个神经网络想象成一个由多层“加工厂”组成的流水线。每一层“加工厂”接收上一层的输出作为输入，进行某种形式的“加工”后再传递给下一层。

在每个神经元中都将进行一系列的转换 (Transformation):

1. 线性组合 (Linear Combination)：将输入信号（来自上一层神经元的输出）进行加权求和。
2. 非线性转换 (Non-linear Transformation)：将加权求和的结果通过一个激活函数 (Activation Function) 进行转换

神经网络的最终输出，就是经过多层这样的线性组合和非线性转换后得到的结果。

神经网络的学习目标是找到合适的网络权重（连接神经元之间的权重），使得网络的输出能够尽可能地接近真实值。这个寻找最优权重的过程，通常使用梯度下降 (Gradient Descent) 算法。沿着误差函数（衡量网络输出与真实值之间差距的函数）梯度下降最快的方向，不断调整网络权重，最终找到误差函数的最小值点，此时的权重就是我们学习到的最优权重。

学习率(Learning Rate) 是梯度下降算法中的一个非常重要的超参数，它决定了每次更新权重时，沿着梯度方向前进的步长大小。

• 学习率过大：可能导致模型在误差函数的最小值附近震荡，无法收敛到最优解，甚至可能发散。
• 学习率过小：会导致模型收敛速度过慢，训练时间过长。

因此，选择一个合适的学习率对于神经网络的训练至关重要。通常需要通过实验来找到一个比较好的学习率。

为了高效地计算误差函数对每个权重的梯度，神经网络中使用了反向传播 (Backpropagation) 算法。反向传播 (Backpropagation) 算法是训练神经网络的核心算法。它的主要思想是利用链式法则 (Chain Rule)，高效地计算神经网络中误差函数 (Error Function) 对每个权重 (Weight) 的偏导数，即梯度。

我们可以从输出层开始，逐步向后计算每一层的梯度。有了这些梯度，我们就可以使用梯度下降等优化算法来更新权重，从而最小化误差函数。

假设我们有一个神经网络，最后一层是输出层。从输出层来看，我们假设每个样本神经网络预测值与实际值之间的平方误差为：$e_n=(y_n-NNet(\mathbf{x_n}))^2$

在输出层，网络的输出 $NNet(\mathbf{x_n})$ 等于 $s_1^{(L)}$（假设输出层只有一个神经元且没有激活函数），则：$e_n=(y_n-NNet(\mathbf{x_n}))^2 = (y_n-s_1^{(L)})^2$

对于输出层的某个神经元 $j$ 的一个权重 $w_{ij}^{(L)}$ （连接倒数第二层神经元 $i$ 到输出层神经元 $j$ 的权重），误差函数 $e_n$ 对这个权重的偏导数 $\frac{\partial e_n}{\partial w_{ij}^{(L)}}$ 的计算依赖链式法则。根据链式法则，当一个函数通过中间变量依赖于另一个变量时，它的导数可以通过分解成多个导数的乘积来计算。 在这里，误差 $e_n$ 通过输出层神经元的分数 $s_1^{(L)}$ 依赖于权重 $w_{i1}^{(L)}$。 因此，我们可以将 $\frac{\partial E_n}{\partial w_{i1}^{(L)}}$ 分解为两个偏导数的乘积：

其中：

• $e_n$ 是第 $n$ 个样本的误差。
• $s_1^{(L)}$ 是输出层第 $1$ 个神经元的分数 (score)，也就是该神经元线性组合的输出，尚未经过激活函数。
• $w_{ij}^{(L)}$ 是连接倒数第二层神经元 $i$ 到 输出层 神经元 $j$ 的权重。

接下来就是分别计算 $\frac{\partial e_n}{\partial s_1^{(L)}}$ 和 $\frac{\partial s_1^{(L)}}{\partial w_{i1}^{(L)}}$。

我们对 $s_1^{(L)}$ 求偏导数：

应用链式法则，令 $u = y_n - s_1^{(L)}$，则 $\frac{du}{ds_1^{(L)}} = -1$，所以：

接下里计算 $\frac{\partial s_1^{(L)}}{\partial w_{i1}^{(L)}}$，输出层神经元的分数 $s_1^{(L)}$ 是前一层神经元输出的线性组合:

其中，$w_{i1}^{(L)}$ 是连接倒数第二层（$L-1$层）的第 $i$ 个神经元到输出层（$L$层）第 $1$ 个神经元的权重，$x_i^{(L-1)}$ 是倒数第二层第 $i$ 个神经元的输出。现在我们对 $w_{i1}^{(L)}$ 求偏导数。在求和项中，只有包含 $w_{i1}^{(L)}$ 的项才与 $w_{i1}^{(L)}$ 相关，其他项的偏导数为 0。因此：

最后，带入公式得到：

可以看到，输出层权重的梯度与误差项 $(y_n - s_1^{(L)})$ 以及前一层的输出 $x_i^{(L-1)}$ 有关。

对于隐藏层的权重，计算过程会稍微复杂一些。假设我们要计算第 $l$ 层（不是输出层）的某个权重 $w_{ij}^{(l)}$ （连接第 $l-1$ 层神经元 $i$ 到第 $l$ 层神经元 $j$ 的权重）的梯度 $\frac{\partial e_n}{\partial w_{ij}^{(l)}}$。

此时我们使用一个中间变量 $\delta_j^{(l)}$，表示误差函数 $e_n$ 对第 $l$ 层第 $j$ 个神经元的分数 $s_j^{(l)}$ 的偏导数：

利用链式法则，我们可以得到隐藏层权重的梯度计算公式：

至于计算 $\delta_j^{(l)}$，可以使用一些递推关系做一些中间变量替换处理，因为相对复杂，这里就不详细解释了。

总结一下，反向传播算法的过程主要包括以下几个步骤：

1. 前向传播 (Forward Propagation)：将输入数据输入网络，逐层计算每个神经元的激活值，直到输出层，得到网络的预测结果。
2. 计算输出层误差 (Calculate Output Layer Error)：根据网络的预测结果和真实标签，计算输出层的误差。
3. 反向传播 (Backward Propagation)：从输出层开始，反向逐层计算误差对每个权重的偏导数（梯度）。计算输出层的 $\delta$ 值，利用 $\delta$ 的递推关系，从输出层开始，反向逐层计算每一层的 $\delta$ 值，根据公式 $\frac{\partial e_n}{\partial w_{ij}^{(l)}} = \delta_j^{(l)} \cdot x_i^{(l-1)}$ 计算每一层权重的梯度。
4. 更新权重 (Update Weights)：使用计算得到的梯度，利用梯度下降等优化算法更新网络的权重。

为了防止神经网络在训练过程中发生过拟合，我们需要使用一些正则化方法来约束模型的复杂度。Dropout 是一种简单而有效的正则化技术，在神经网络的训练过程中，对于每个训练样本，我们以一定的概率随机地将一部分神经元的输出设置为 0，相当于暂时将这些神经元从网络中“丢弃”。

这样做的好处是：

1. 减少神经元之间的依赖：因为每次训练都会随机地丢弃一部分神经元，所以网络不会过度依赖于某些特定的神经元，从而提高网络的泛化能力。
2. 相当于训练多个子网络：每次丢弃一部分神经元，相当于在训练一个不同的子网络。Dropout 可以看作是一种模型集成的思想，将多个子网络的预测结果进行平均，从而提高预测的准确性。

PLA Process#

感知机学习算法（Perceptron Learning Algorithm, PLA） 是一种用于 二元分类 的算法，目标是找到一个超平面（在二维空间中是一条直线），将两类数据点分开。具体来说，给定一组训练数据：$D = \{ (x_1, y_1), (x_2, y_2), \dots, (x_N, y_N) \}$，其中 $x_i$ 是输入特征，$y_i \in \{ +1, -1 \}$ 是标签，PLA 的目标是找到一个权重向量 $w$，使得：

PLA 的核心思想是 迭代修正：从初始权重向量 $w_0$ 开始，逐步修正分类错误的点，直到所有点都被正确分类。

1. 初始化：选择一个初始权重向量 $w_0$，并设置$w_0 = 0$。
2. 循环迭代修正：遍历所有数据点，找到第一个分类错误的点
   • 找到当前权重向量 $w_t$ 分类错误的点 $(x_n, y_n)$，满足 $\text{sign}(w_t^T x_n) \neq y_n$。
   • 更新权重向量：$\mathbf{w}_{t+1} \leftarrow \mathbf{w}_t + y_n \mathbf{x}_n$
     • 如果真实标签 $y_n = +1$，但预测为 -1（即 $\mathbf{w}_t^T \mathbf{x}_n < 0$），则将权重向量向 $\mathbf{x}_n$ 的方向移动，使得 $\mathbf{w}_{t+1}^T \mathbf{x}_n$ 更可能大于 0。
     • 如果真实标签 $y_n = -1$，但预测为 +1（即 $\mathbf{w}_t^T \mathbf{x}_n > 0$），则将权重向量向 $-\mathbf{x}_n$ 的方向移动，使得 $\mathbf{w}_{t+1}^T \mathbf{x}_n$ 更可能小于 0。
   • 重复上述过程，直到所有点都被正确分类。
3. 终止条件：当完成一次完整的数据集遍历后，没有发生任何分类错误，则算法终止，当前的权重向量 $\mathbf{w}$ 就是我们找到的能够完美分割数据的超平面的参数。

接下来我们通过一个例子来深入理解PLA的迭代修正。

假设我们有以下数据集：

初始化：为了方便计算，我们添加偏置项 $x_0 = 1$，所以样本点的表示变为 $(x_0, x_1, x_2)$。我们初始化权重向量 $\mathbf{w}_0 = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}$。

循环迭代：

1. 第一次迭代：

   1. 样本 1: (1, 1, 1), y = +1：预测：$\mathbf{w}_0^T \mathbf{x}_1 = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} = 0$， $sign(0)$ 可以定义为 +1 或 -1，假设我们定义为 +1。分类正确。

   2. 样本 2: (1, 2, 3), y = +1：预测：$\mathbf{w}_0^T \mathbf{x}_2 = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = 0$，分类正确。

   3. 样本 3: (1, 3, 1), y = +1：预测：$\mathbf{w}_0^T \mathbf{x}_3 = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 3 \\ 1 \end{bmatrix} = 0$，分类正确。

   4. 样本 4: (1, 1, 3), y = -1：预测：$\mathbf{w}_0^T \mathbf{x}_4 = \begin{bmatrix} 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 3 \end{bmatrix} = 0$，假设分类为 +1 (与真实标签 -1 不同)，分类错误。

      更新权重：$\mathbf{w}_1 = \mathbf{w}_0 + y_4 \mathbf{x}_4 = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} + (-1) \begin{bmatrix} 1 \\ 1 \\ 3 \end{bmatrix} = \begin{bmatrix} -1 \\ -1 \\ -3 \end{bmatrix}$。

   5. 样本 5: (1, 2, -1), y = -1：预测：$\mathbf{w}_1^T \mathbf{x}_5 = \begin{bmatrix} -1 & -1 & -3 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ -1 \end{bmatrix} = -1 - 2 + 3 = 0$，假设分类为 +1 (与真实标签 -1 不同)，分类错误。

      更新权重：$\mathbf{w}_2 = \mathbf{w}_1 + y_5 \mathbf{x}_5 = \begin{bmatrix} -1 \\ -1 \\ -3 \end{bmatrix} + (-1) \begin{bmatrix} 1 \\ 2 \\ -1 \end{bmatrix} = \begin{bmatrix} -2 \\ -3 \\ -2 \end{bmatrix}$。

2. 第二次迭代：

   1. 样本 1: (1, 1, 1), y = +1

      预测：$\mathbf{w}_2^T \mathbf{x}_1 = \begin{bmatrix} -2 & -3 & -2 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} = -2 - 3 - 2 = -7$，分类为 -1，分类错误。

      更新权重：$\mathbf{w}_3 = \mathbf{w}_2 + y_1 \mathbf{x}_1 = \begin{bmatrix} -2 \\ -3 \\ -2 \end{bmatrix} + (+1) \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} -1 \\ -2 \\ -1 \end{bmatrix}$。

   2. 样本 2: (1, 2, 3), y = +1

      预测：$\mathbf{w}_3^T \mathbf{x}_2 = \begin{bmatrix} -1 & -2 & -1 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = -1 - 4 - 3 = -8$，分类为 -1，分类错误。

      更新权重：$\mathbf{w}_4 = \mathbf{w}_3 + y_2 \mathbf{x}_2 = \begin{bmatrix} -1 \\ -2 \\ -1 \end{bmatrix} + (+1) \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 2 \end{bmatrix}$。

   3. 样本 3: (1, 3, 1), y = +1

      预测：$\mathbf{w}_4^T \mathbf{x}_3 = \begin{bmatrix} 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} 1 \\ 3 \\ 1 \end{bmatrix} = 0 + 0 + 2 = 2$，分类为 +1，分类正确。

   4. 样本 4: (1, 1, 3), y = -1

      预测：$\mathbf{w}_4^T \mathbf{x}_4 = \begin{bmatrix} 0 & 0 & 2 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 3 \end{bmatrix} = 0 + 0 + 6 = 6$，分类为 +1，分类错误。

      更新权重：$\mathbf{w}_5 = \mathbf{w}_4 + y_4 \mathbf{x}_4 = \begin{bmatrix} 0 \\ 0 \\ 2 \end{bmatrix} + (-1) \begin{bmatrix} 1 \\ 1 \\ 3 \end{bmatrix} = \begin{bmatrix} -1 \\ -1 \\ -1 \end{bmatrix}$。

   5. 样本 5: (1, 2, -1), y = -1

      预测：$\mathbf{w}_5^T \mathbf{x}_5 = \begin{bmatrix} -1 & -1 & -1 \end{bmatrix} \begin{bmatrix} 1 \\ 2 \\ -1 \end{bmatrix} = -1 - 2 + 1 = -2$，分类为 -1，分类正确。

3. 继续进行迭代，直到所有样本都被正确分类。假设经过若干次迭代后，我们得到一个权重向量 $\mathbf{w} = \begin{bmatrix} a \\ b \\ c \end{bmatrix}$，它可以正确分类所有样本。