1588 字

8 分钟

【算法设计与分析】二叉搜索树

2023-05-17

2023-05-26

学习笔记/算法设计与分析

algorithm

/

二叉搜索树

前言#

经过之前数据结构的学习，我们知道如果一个二叉树满足：

若其左子树非空，则左子树上所有节点各自的值都小于根节点的值
若其右子树非空，则右子树上所有节点各自的值都大于根节点的值
其左右子树都是一棵二叉查找树。

则它是一个 二叉搜索树(Binary Search Trees, BST) 。

遍历顺序#

对树的遍历，我们来复习一下：

先序遍历#

在先序遍历中，对节点的处理工作是在它的诸儿子节点被处理之前(pre)进行的。

先序遍历步骤为：访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。即根左右。

例如下面的这个树：

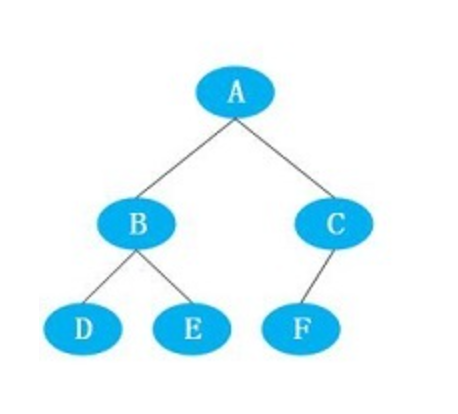
它遍历的顺序就是ABDECF

后续遍历#

和先续遍历不同的是它的访问不是我们所想的从跟开始，而是从左开始：

后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。即左右根。

例如之前的这个树：它遍历的顺序就是DEBFCA

因此我们可以发现，这个先和后，指的是跟的先后。

中序遍历#

在二叉树中还有一种中序遍历，按照我们之前的说法，它是跟的中序：中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。即左根右。

故之前的那颗树的遍历顺序是：DBEAFC

如果我们使用设这个BST是T，x是二叉搜索树中的一个结点。如果y是左子树中的一个结点，那么 y.key ≤ x.key；如果y是右子树中的一个结点，那么 y.key ≥ x.key。那么中序遍历的伪代码为：

1
INORDER-TREE-WALK(x)
2
    if x ≠ NIL
3
        INORDER-TREE-WALK(x.left)
4
        print x.key
5
        INORDER-TREE-WALK(x.right)
6

7
INORDER-TREE-WALK(T.root)  //从根结点开始

如果x是一棵有n个结点的子树的根，那么调用INORDER-TREE-WALK(x)运行时间 $O(n)$ ，证明省略。

查找BST#

二叉搜索树支持SEARCH、MINIMUM、MAXIMUM、PREDECESSOR、SUCCESSOR等查询操作。在一棵高度为 h 的二叉搜索树上，SEARCH、MINIMUM、MAXIMUM、PREDECESSOR和SUCCESSOR的运行时间为 $O(h)$ 。

查找(Searching)#

1
TREE-SEARCH(x, k)
2
    if x == NIL or k == x.key
3
        return x
4
    if k < x.key
5
        return TREE-SEARCH(x.left, k)
6
    else return TREE-SEARCH(x.right, k)
7

8
TREE-SEARCH(T.root, k)

TREE-SEARCH的运行时间为 $O(h)$ ，其中 h 为树的高度。

关键字最小元素和关键字最大元素 (Minimum and maximum)#

1
TREE-MINIMUM(x)
2
    while x.left ≠ NIL
3
        x = x.left
4
    return x
5

6
TREE-MAXIMUM(x)
7
    while x.right ≠ NIL
8
        x = x.right
9
    return x

TREE-MINIMUM和TREE-MAXIMUM的运行时间均为 $O(h)$ ，其中 h 为树的高度.

后继和前驱(Successor and predecessor)#

1
TREE-SUCCESSOR(x)
2
    if x.right ≠ NIL
3
        return TREE-MINIMUM(x.right)  // leftmost node in right subtree
4
    else // find the lowest ancestor of x whose left child is an ancestor of x
5
        y = x.p
6
        while y ≠ NIL and x == y.right
7
            x = y
8
            y = y.p
9
        return y
10

11
TREE-PREDECESSOR(x)
12
    if x.left ≠ NIL
13
        return TREE-MAXIMUM(x.left)  // rightmost node in left subtree
14
    else // find the highest ancestor of x whose right child is an ancestor of x
15
        y = x.p
16
        while y ≠ NIL and x == y.left
17
            x = y
18
            y = y.p
19
        return y

TREE-MINIMUM和TREE-MAXIMUM的运行时间均为 $O(h)$ ，其中为树的高度。

插入和删除(Insertion and deletion)#

具体插入与删除的解析，请见：

https://hoyue.fun/data_structure_3.html#Insert

插入和删除操作会引起二叉搜索树表示的动态集合的变化，但是二叉搜索树的性质保持不变。在一棵高度为 h的二又搜索树上，INSERT和DELETE的运行时间为 $O(h)$ 。

插入#

向二叉搜索树T中插入结点z，其关键字为 z.key ，伪代码TREE-INSERT如下

1
TREE-INSERT(T, z)
2
    x = T.root  // node being compared with z
3
    y = NIL  // y will be parent of z
4
    while x ≠ NIL  // descend until reaching a leaf
5
        y = x
6
        if z.key < x.key
7
            x = x.left
8
        else x = x.right
9
    z.p = y  // found the location - insert z with parent y
10
    if y == NIL
11
        T.root = z  // tree T was empty
12
    else if z.key < y.key
13
        y.left = z
14
    else y.right = z

该过程保持跟踪指针(trailing pointer) y 记录 x 的父结点，TREE-INSERT的运行时间为 $O(h)$ ，其中h为的高度。

删除#

从二叉搜索树 T 中删除结点 z 分三种情况

情况一: 如果z没有孩子结点，直接删除， z 的父结点指向z的指针置为NIL。
情况二: 如果z只有一个孩子结点，将这个孩子结点提升到z的位置，z 的父结点指向z的指针改为指向这个孩子结点。
情况三: 如果z有两个孩子结点，找出z的后继 y，让y占据z的位置，z 的右子树变为 y的右子树，z 的左子树变为 y 的右子树。由于y是z的后继，所以y不可能有孩子。
- 如果y 是z的右孩子，用y 替换z。
- 如果y在2的右子树中且y 不是z 的右孩子，先用y 的右孩子结点替换 y，然后用y 替换 z。

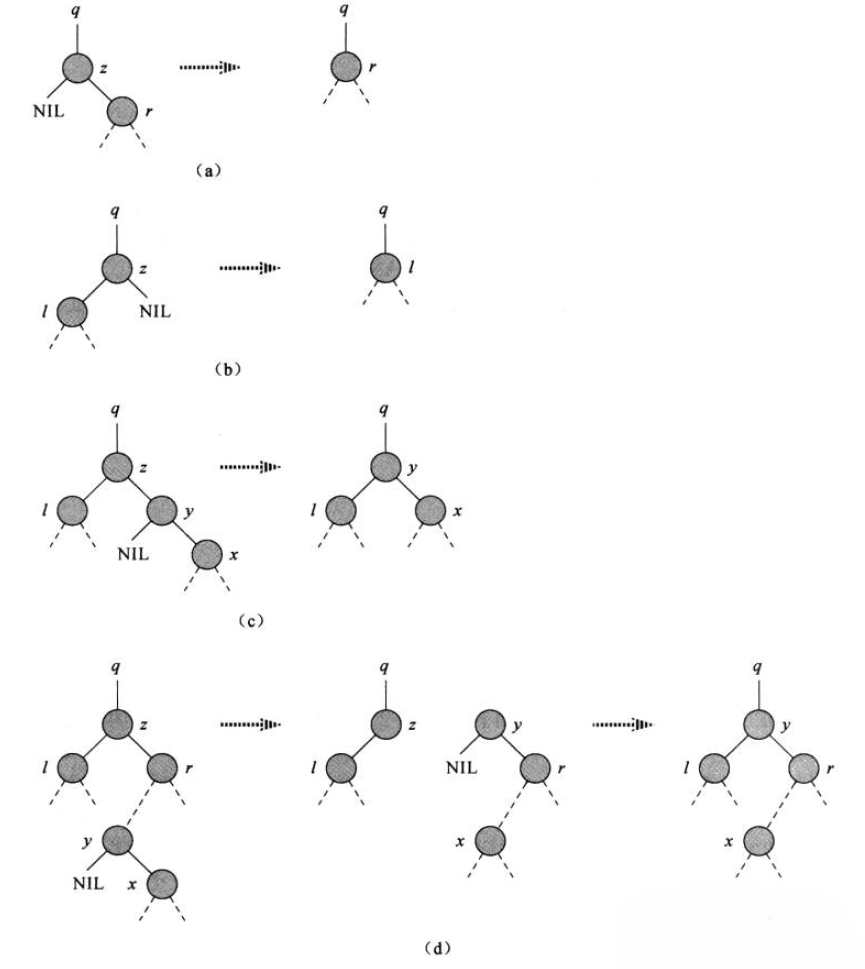
子程序TRANSPLANT实现了用某子树原先父结点的指向该子树的指针指向另一棵子树，实现了子树的替换。伪代码如下:

1
TRANSPLANT(T, u, v)
2
    if u.p == NIL
3
        T.root = v
4
    else if u == u.p.left
5
        u.p.left = v
6
    else u.p.right = v
7
    if v ≠ NIL
8
        v.p = u.p

1
TREE-DELETE(T, z)
2
    if z.left == NIL
3
        TRANSPLANT(T, z, z.right)    // replace z by its right child
4
    else if z.right == NIL
5
        TRANSPLANT(T, z, z.left)    // replace z by its left child
6
    else y = TREE_MINIMUM(z.right)    // y is z's successor
7
        if y ≠ z.right    // is y farther down the tree?
8
            TRANSPLANT(T, y, y.right)    // replace y by its right child
9
            y.right = z.right
10
            y.right.p = y    // z's right child becomes y's right child
11
        TRANSPLANT(T, z, y)    // replace z by its successor y
12
        y.left = z.left
13
        y.left.p = y    // and give z's left child to y which had no left child

TREE-DELETE的运行时间为 $O(h)$ ，其中h为树的高度。

后记#

本文介绍了二叉搜索树(Binary Search Trees, BST)的定义和遍历顺序，包括先序遍历、后序遍历和中序遍历。同时，还介绍了BST的查找操作，包括SEARCH、MINIMUM、MAXIMUM、PREDECESSOR和SUCCESSOR等查询操作。文章还讲解了BST的插入和删除操作，包括向BST中插入结点和从BST中删除结点的实现方法。在一棵高度为 h 的BST上，SEARCH、MINIMUM、MAXIMUM、PREDECESSOR、SUCCESSOR、INSERT和DELETE的运行时间均为 $O(h)$ 。