最优子结构#

用动态规划求解问题的第一步是描述最优解的结构特征。问题的最优解包含子问题的最优解。如果一个问题能够表现出最优子结构特征，那么它可能能够用动态规划求解。

重叠子问题#

适合用动态规划求解问题的第二个特征是子问题空间足够小，这样才能够产生足够的相同的子问题。递归算法会反复求解相同的子问题，而不是一直生成新的子问题。一般来说，不同子问题总数是输入规模的多项式函数。如果递归过程能够反复求解相同的子问题，就称最优化问题具有重叠子问题性质。动态规划利用重叠子问题性质，对每个子问题只需要求解一次，并将解存入表格中，再次求解该子问题时可以直接查表，每次查表的时间代价为常量。

问题解析#

假定我们正在设计一个程序，实现英语文本到法语的翻译。对英语文本中出现的每个单词，我们需要查找对应的法语单词。为了实现这些查找操作，我们可以创建一棵二叉搜索树，将n个英语单词作为关键字，对应的法语单词作为关联数据。由于对文本中的每个单词都要进行搜索，我们希望花费在搜索上的总时间尽量少。我们可以假定每次搜索时间为 $O(\lg n)$ 。

但是，单词出现的频率是不同的，像”the”这种频繁使用的单词有可能位于搜索树中远离根的位置上，而像”machicolation”这种很少使用的单词可能位于靠近根的位置上。这样的结构会减慢翻译的速度，因为在二叉树搜索树中搜索一个关键字需要访问的结点数等于包含关键字的结点的深度加 1（根结点）。

我们希望文本中频繁出现的单词被置于靠近根的位置而且，文本中的一些单词可能没有对应的法语单词，这些单词根本不应该出现在二叉搜索树中。在给定单词出现频率的前提下，我们应该如何组织一棵二叉搜索树，使得所有搜索操作访问的结点总数最少呢?

这个问题称为 最优二叉搜索树 (optimal binary search tree)问题。定义如下：给定一个有n个不同关键字的已排序的序列 $K=(k_1, k_2, \ldots, k_n)$ (因此 $k_1 < k_2 < \ldots < k_n$ )，我们希望用这些关键字构造一棵二叉搜索树。

对每个关键字 $k_i$ ，都有一个概率 $p_i$ 表示其搜索频率。有些要搜索的值可能不在K中，因此我们还有n+1个”伪关键字” $d_0, d_1, d_2, \ldots, d_n$ 表示不在K中的值。 $d_0$ 表示所有小于 $k_1$ 的值， $d_n$ 表示所有大于 $k_n$ 的值，而 $k_i < d_i < k_{i+1}$ 。对于每个不在K中的关键字 $d_i$ ，它的搜索概率为 $q_i$ 。

每个关键字 $k_i$ 对应二叉搜索树中一个内部结点，每个虚关键字 $d_i$ 对应二叉搜索树中一个叶结点，这样每次查找关键字如果查找成功，那么最终落在 $k_i$ ，如果查找失败，那么最终落在 $d_i$ 。

查找成功概率为 $p_i$ ，失败概率为 $q_i$ ，于是根据概率知识可以知道：

$\sum_{i=1}^{n} p_i + \sum_{i=0}^{n} q_i = 1$

那么，我们可以计算它们的消耗代价，下面举一些实体例子，已知存在5个关键字和6个伪关键字如下表：

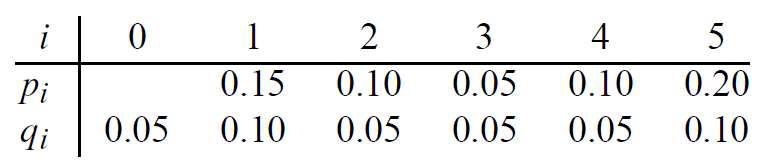
我们构造两颗二叉搜索树如图：

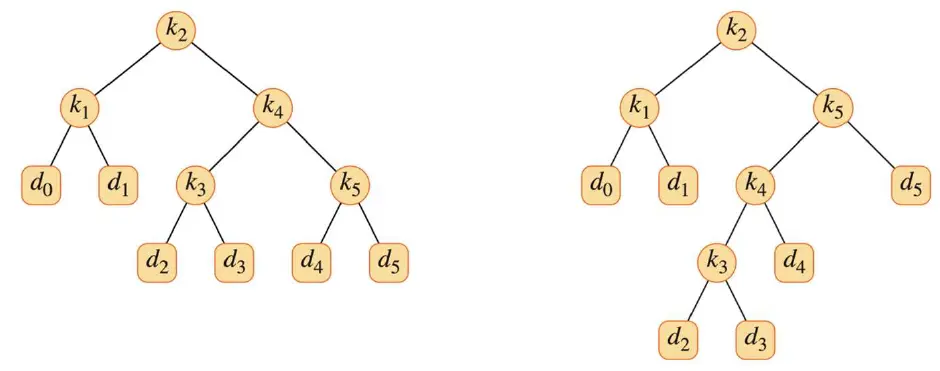
由于我们知道每个关键字和伪关键字的搜索概率，因而可以确定在一棵给定的二叉搜索树T中进行一次搜索的期望代价。假定一次搜索的代价等于访问的结点数，即此次搜索找到的结点在树中的深度再加1。那么在树中进行一次搜索的期望代价分别为:

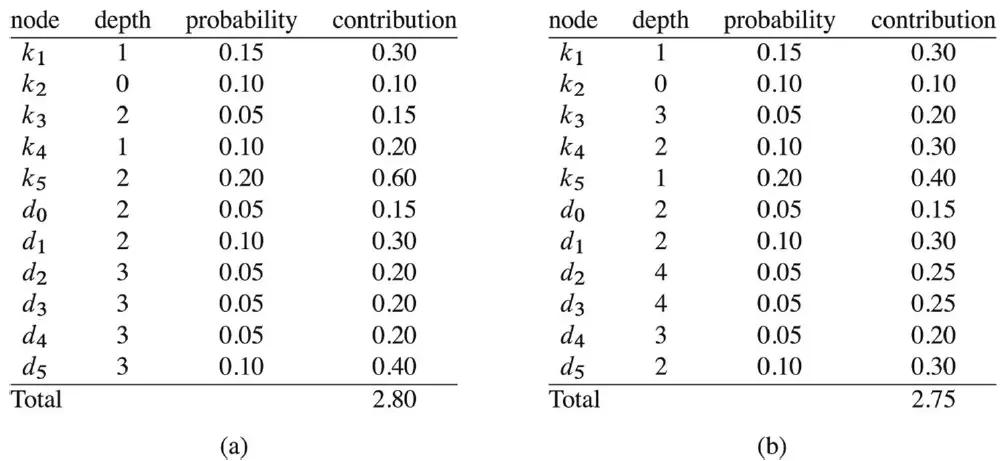
如图(a)， $k_1$ 的代价为深度+1 = 2， $(1+1) \times p_1 = 2 \times 0.15 = 0.3$ ，其他的类推。

对比左右两个表，可以看到右表对应的右边的树消耗代价更少，它比左边的树更优。推导一个通式得：

于是我们可以给这个问题一个定义：对于一个给定的概率集合，我们希望构造一棵期望搜索代价最小的二叉搜索树，我们称之为 最优二叉搜索树 。

从上述的例子中可以知道，最优二叉搜索树不一定是高度最矮的。而且，概率最高的关键字也不一定出现在二叉搜索树的根结点( $k_5$ 概率最高，但是例子中以 $k_2$ 作为root)。穷举并检查所有可能的二叉搜索树不是一个高效的算法。接下来就是对它的动态规划分析。

Step 1：最优二叉搜索树的结构#

给定一棵二叉搜索树，考虑其中任意一棵 子树 ，设它包含关键字 $k_i, \ldots, k_j$ ，其中 $1 \leq i \leq j \leq n$ 。同时，子树有包含虚关键字 $d_{i-1}, d_i, \ldots, d_j$ 的叶结点。

[task]如果一棵最优二叉搜索树 T 有一棵包含关键字 $k_i, \ldots, k_j$ 的子树 T’ ，那么 T’ 一定是包含关键字 $k_i, \ldots, k_j$ 和虚关键字 $d_{i-1}, d_i, \ldots, d_j$ 的子问题的最优解。[/task]

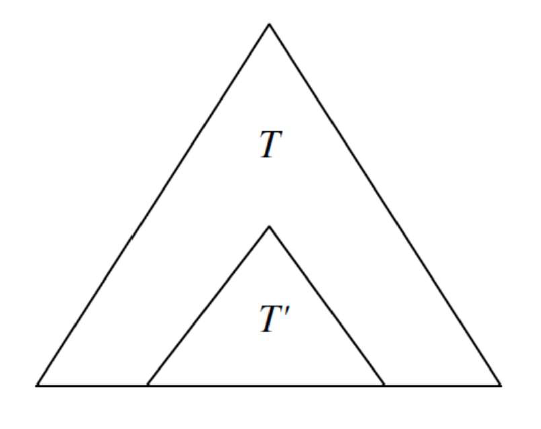
我们需要利用最优子结构性质来证明，我们可以用子问题的最优解构造原问题的最优解。给定关键字 $k_i, \ldots, k_j$ ，选择其中的一个关键字例如 $k_r$ 作为最优子树的根结点。根据BST的性质，在根节点左侧的子树都小于根节点，右侧的子树都大于根节点。

那么左子树就包含关键字 $k_i, \ldots, k_{r-1}$ ，右子树则包含 $k_{r+1}, \ldots, k_j$ 关键字，伪关键字同理。只要我们检查所有可能的根结点 $k$ ( $i \leq r \leq j$ )，并对每种情况分别求解包含关键字 $k_i, \ldots, k_{r-1}$ ，和包含 $k_{r+1}, \ldots, k_j$ 关键字的最优二叉搜索树即可找到最优解。

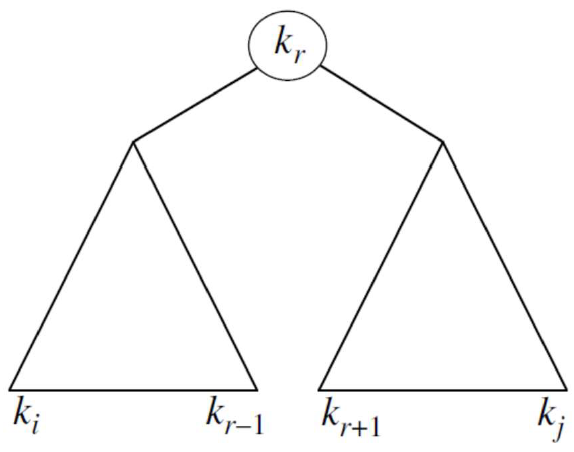
于是我们就找到了一个最小的结构，即T’，之后将对每个T’进行求解。

Step 2：一个递归算法#

我们在上一步选取的子问题是：求解一个子树T’，它满足包含关键字 $k_i, \ldots, k_j$ ，其中 $1 \leq i \leq j \leq n$ 。同时，子树有包含虚关键字 $d_{i-1}, d_i, \ldots, d_j$ 的叶结点。

我们定义一个期望代价 e[i, j] ，并整体表达为 e[1, n] 。

[task] e[i, j] 为在包含关键字 $k_i, \ldots, k_j$ 的最优二叉搜索树中进行一次关键字搜索的期望代价。[/task]

先从特殊的情况开始，当 $j = i - 1$ 时，此时表示关键字 $k_i$ 到 $k_j$ 之间没有任何关键字。表示关键字 $k_i, \ldots, k_j$ 中没有任何一个关键字。因此我们需要插入虚关键字 $d_{i-1}$ ( $k_{i-1} < d_{i-1} < k_i$ )，使得它成为子树的唯一叶结点。

对于这种情况，我们可以直接计算搜索代价。那么很容易得到这种情况下， e[i, i-1] = $q_{i-1}$ 。

当 $j \geq i$ 时，对于这个情况，设 $k_r$ 作为子树 T’ 的根结点。那么左子树就包含关键字 $k_i, \ldots, k_{r-1}$ ，右子树则包含 $k_{r+1}, \ldots, k_j$ 关键字，伪关键字同理。当一棵树成为一个结点的一个子树时，树中所有结点的深度都要加一。

根据我们在上面写的代价通式：

$E[\text{search cost in } T] = \sum_{i=1}^{n} (\text{depth}_T(k_i) + 1) \cdot p_i + \sum_{i=0}^{n} (\text{depth}_T(d_i) + 1) \cdot q_i$

[task]包含关键字 $k_i, \ldots, k_j$ 的子树，定义子树中所有关键字和虚关键字的概率和为 w(i, j) 。[/task]

即， w(i, j) 的式子为：

$w(i, j) = \sum_{l=i}^{j} p_l + \sum_{l=i-1}^{j} q_l$

若 $k_r$ 作为子树 T’ 的根结点，我们可以得到这样的递推式：

e[i, j] = $p_r$ + (e[i, r-1] + w(i, r-1)) + (e[r+1, j] + w(r+1, j))

将 w(i, j) 用递推改编一下得： w(i, j) = w(i, r-1) + $p_r$ + w(r+1, j)

因此带入e[i, j]中得：

假定我们知道哪个结点应该作为根结点。如果选取期望搜索代价最低者作为根结点，可得最终递归公式：

为了帮助构造最优解，我们添加下列定义到任务列表中：

[task]定义root[i, j]保存包含关键字 $k_i, \ldots, k_j$ 的最优二叉树的根结点关键字k的下标r（并非e[i, j]）。[/task]

Step 3：计算最优二叉搜索树的期望搜索代价#

我们在上面分析得到了期望代价的动态转移方程。

我们可以将 e[i, j] 保存在表格 e[1:n+1, 0:n] ，其中行索引表示关键字的起始位置i，列索引表示关键字的结束位置j。第一个下标1到n+1是因为需要考虑只有 $d_n$ 的情况，即 e[n+1, n] (when j = i - 1) ，第二个下标从0开始是因为需要考虑只有 $d_0$ 的情况，即 e[1,0] (when j = i - 1)

为了避免每次计算 e[i, j] 时花费 $\Theta(j - i)$ 次加法重新计算 w(i, j) ，将 w 保存在表格 w[1:n+1, 0:n] ，同 e[i, j] ，我们也可以通过两个情况得到它的递归式：

表格w总共有 $\Theta(n^2)$ 个表项，每个表项的计算时间为 $O(1)$ 。

我们只使用表中满足 $j \geq i-1$ 的表项 e[i, j] 。我们还使用一个表 root ，表项 root[i, j] 记录包含关键字 $k_i, \ldots, k_j$ 的子树的根。我们只使用此表中满足 $1 \leq i \leq j \leq n$ 的表项 root[i, j] 。

程序OPTIMAL-BST输入为概率表 $p_1, \ldots, p_n$ 和 $q_0, q_1, \ldots, q_n$ 以及规模 n ，输出表格 e 和 root 伪代码如下:

1
OPTIMAL-BST(p, q, n)
2
    let e[1 : n + 1, 0 : n], w[1 : n + 1, 0 : n], and root[1 : n, 1 : n] be new tables
3
    for i = 1 to n + 1    // base cases
4
        e[i, i - 1] = q_{i-1}    // equation (14.14)
5
        w[i, i - 1] = q_{i-1}
6
    for l = 1 to n
7
        for i = 1 to n - l + 1
8
            j = i + l - 1
9
            e[i, j] = ∞
10
            w[i, j] = w[i, j - 1] + p_j + q_j    // equation (14.15)
11
            for r = i to j     // try all possibles roots r
12
                t = e[i, r - 1] + e[r + 1, j] + w[i, j]    //equation (14.14)
13
                if t < e[i, j]    // new minimum?
14
                    e[i, j] = t
15
                    root[i, j] = r
16
    return e and root

• 第2~4行的for循环初始化 e[i，i - 1] 和 w(i, i - 1) 的值；
• 第5~14行的for循环利用e的递归式和w的递归式来对所有 $1 \leq i \leq j \leq n$ 计算 e[i, j] 和 w(i, j) 。
• 在第一个循环步中，l=1，循环对所有i=1, 2, …, n - 1计算 e[i, i] 和 w(i, i) 。
• 第二个循环步中，l=2，对所有i=1, 2, …, n - 1计算 e[i, i+1] 和 w(i, i+1) ，依此类推。
• 第10~14行的内层for循环，逐个尝试下标r，确定哪个关键字点作为根结点可以得到包含关键字 $k_i, \ldots, k_j$ 的最优二叉搜索树。这个for循环在找到更好的关键字作为根结点时，会将其下标r保存在 root[i, j] 中。

理解这个算法以后，我们就可以来一步步求解最优二叉搜索树了。

填表过程#

我们先把已知条件摆出来：

递归子问题：

如果一棵最优二叉搜索树 T 有一棵包含关键字 $k_i, \ldots, k_j$ 的子树 T’ ，那么 T’ 一定是包含关键字 $k_i, \ldots, k_j$ 和虚关键字 $d_{i-1}, d_i, \ldots, d_j$ 的子问题的最优解。

表定义：

e[i, j] 为在包含关键字 $k_i, \ldots, k_j$ 的最优二叉搜索树中进行一次关键字搜索的期望代价。

包含关键字 $k_i, \ldots, k_j$ 的子树，定义子树中所有关键字和虚关键字的概率和为 w(i, j) 。

定义root[i, j]保存包含关键字 $k_i, \ldots, k_j$ 的最优二叉树的根结点关键字k的下标r（并非e[i, j]）。

概率表：

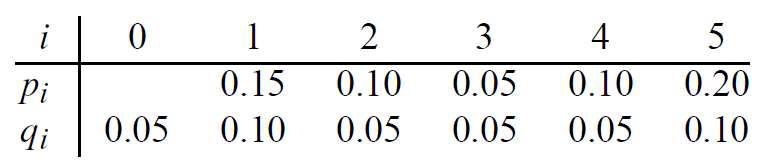
有了这些内容，我们就可以根据算法进行填表了。

首先是w表，它是最显而易见的。它的公式为：

首先将所有 $j = i -1$ 的情况赋予特殊值 $q_{i-1}$ .（对角线填值）

1
for i = 1 to n + 1
2
        w[i, i - 1] = q_{i-1}

然后再对 $j \geq i$ 的情况使用公式中递归的填表。

1
for l = 1 to n
2
        for i = 1 to n - l + 1
3
            j = i + l - 1
4
            w[i, j] = w[i, j - 1] + p_j + q_j

很容易填出如下表（没涉及到的位置就不填）：

总结一下填表规律：

• 首先先填对角线，填入 $q_i$ 的所有内容。
• 然后在填已填写位置右侧的一格（例如已填写w[1,0], 那么接下来就填w[1,1]），它的内容根据公式等于左侧单元格内容 + 当前列号(j)对应的 $p_j$ 和 $q_j$ 的概率和。
• 这是一个向右填表的过程，如果已经到达右边的边上，则不用填。每次要填写的数据都少一个（即第一次填6个，第二次就填5个，因为最后那个已经到达边上）。

于是我们把这个表旋转一下，就可以得到书上的图了：

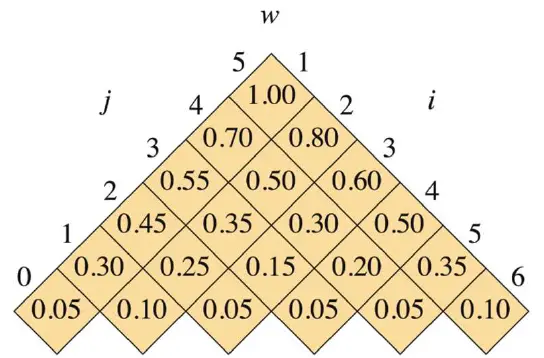
接下来是e表和root表，相对于w表就稍微复杂一点，而root表则是需要根据e表来记录的，e表的公式为：

首先将所有 $j = i -1$ 的情况赋予特殊值 $q_{i-1}$ ，这一点和w表一样：

1
for i = 1 to n + 1
2
        e[i, i - 1] = q_{i-1}

然后 $j \geq i$ 的情况：

1
for l = 1 to n
2
        for i = 1 to n - l + 1
3
            j = i + l - 1
4
            e[i, j] = ∞
5
            for r = i to j     // try all possibles roots r
6
                t = e[i, r - 1] + e[r + 1, j] + w[i, j]
7
                if t < e[i, j]    // new minimum?
8
                    e[i, j] = t
9
                    root[i, j] = r

我们需要寻找的是对于区间[i : j]，找到那个 $r \in [i,j]$ 使得代价最小。初始情况下设置 e[i, j] = ∞ 为一个最大的值，以便寻找最小值替换。每一次找到r都与最小值比较以找到最小的值的下标r，并存在root[i,j]中。

于是我们可以得到如下表，表中填的e[i,j]为最优代价：

填表示例1：如当l=1时，i循环从1-5，j循环也从1-5。那么此时对于e[1,1]，r只能等于1，e[1,1] = e[1,0] + e[2,1] + w[1,1] = 0.05 + 0.1 + 0.3 = 0.45; root r[1,1] = 1.

填表示例2：如当l=2时，i循环从1-4，j循环从2-5。那么此时对于e[4,5]： r = 4，t = e[4, 3] + e[5,5] + w[4,5] = 0.05 + 0.5 + 0.5 = 1.05; r = 5，t = e[4,4] + e[6,5] + w[4,5] = 0.3 + 0.1 + 0.5 = 0.90 < t; 故e[4,5] = t’ = 0.9; root r[4,5] = 5.

填表示例3：当l=4时，i循环从1-2，j循环从4-5，那么对于e[2,5]： r=2 => 0.1+1.3+0.8=2.2; r=3 => 0.4+0.9+0.8=2.1; r=4 => 0.7+0.5+0.8=2.0; r=5 => 1.2+0.1+0.8=2.1; 则选择e[2,5] = 2.0，root r[2,5]=4；

总结一下e表的规律：

• 首先也是对角线的值为 $q_i$ ；
• 之后的值中， r 的取值有 j-i 种，需要每个讨论 j-i 次。
• 每次讨论等价于对位相加。例如第1次讨论则是e表中这一行的第1个数 + e表中这一列的第1个数 + w表中该位置的值。即 对于e[i,j]的第k(k∈[i,j])次讨论，为该行（第i行）的第k个数 + 该列（第j列）的第k个数 + w[i,j] 。
• 对于讨论中相同的值，选择讨论次数k最小的，因为替换最小值时比较为<而不是≤。
• 这个过程也是向右填表，越往后的讨论次数越多。

我们在填e表的过程中，也同时可以完成如下的root表：

同样的，我们翻转一下两个表可以得到：

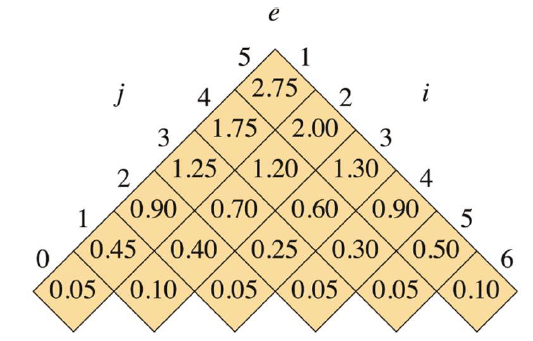
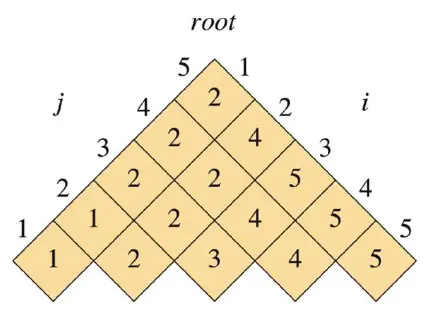
我们得到表了以后，还需要构建最优二叉树，之后就是建树的过程。

Step4：输出最优二叉搜索树的结构#

我们如上图得到了root表，我们可以用这个root表构建最优二叉树，我们有如下算法：

1
CONSTRUCT-OPTIMAL-BST(root,n)
2
    r = root[1,n]
3
    print "k" + r + " is the root"
4
    CONSTRUCT-OPTIMAL-SUBTREE(root,1,r - 1,r,"left")
5
    CONSTRUCT-OPTIMAL-SUBTREE(root,r + 1,n,r,"right")
6

7
CONSTRUCT-OPTIMAL-SUBTREE(root,i,j,r,dir)
8
    if j < i  //若到达叶子结点，放上叶子d
9
      print "d" + j + " is the " + dir + " child of k" + r
10
    else t = root[i, j]
11
      print "k" + t + " is the " + dir + " child of k" + r
12
      CONSTRUCT-OPTIMAL-SUBTREE(root,i,t-1,t,"left")
13
      CONSTRUCT-OPTIMAL-SUBTREE(root,t+1,j,t,"right")

根据这样的算法，我们先从r = root[1,n]知道了整个树的根，然后根的左子树为root[1,r-1]，右子树为[r+1,n]每次都递归找子树的最优根，就可以得到下面的根输出，并构建树：

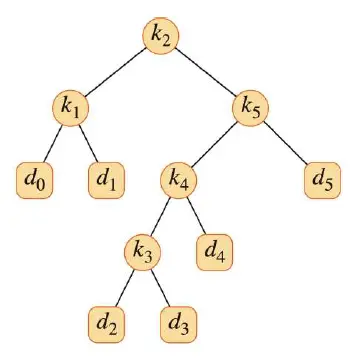
构建的时候也有一些规律：

• 先找k的，如果k已经走投无路了，再回溯。
• 找完所有的k以后，d则是从左向右插入每个k的叶子或空左/右结点中，顺序从0-n。