
前言
对于散列的理解,之前在数据结构中已经非常详细地介绍过了,这里只记录和分析有关的内容。散列表是普通数组概念的推广,数组可以直接寻址, 访问数组中任一元素的时间为O(1) 。
https://hoyue.fun/data_structure_6.html
直接寻址
散列表(hash table)是用来实现字典(dictionary)的有效数据结构,虽然最坏情况下查找一个元素的时间为 ,但平均情况下查找一个元素的时间为 。
非常直观,直接寻址的散列表就是每一个关键字映射到一个直接寻址表的过程。
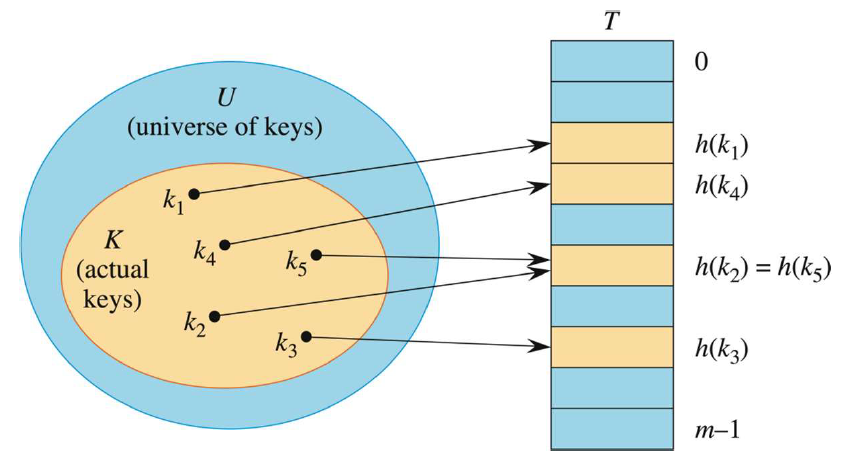
不巧的是,不同数据被插入到相同位置处的时候,会产生冲突 (collision)。 解决冲突的常用方法为分离链接法 (chaining) 和开放寻址法 (opening addressing)。
设直接寻址表为T,它的操作函数有:
DIRECT-ADDRESS-SEARCH(T, k) return T[k]
DIRECT-ADDRESS-INSERT(T, x) T[x.key] = x
DIRECT-ADDRESS-DELETE(T, x) T[x.key] = NIL用于寻址、插入与删除,它们运行时间均为 。
分离链接法
分离链接法,其做法是将散列到同一个值的所有元素保存到一个单链表中。
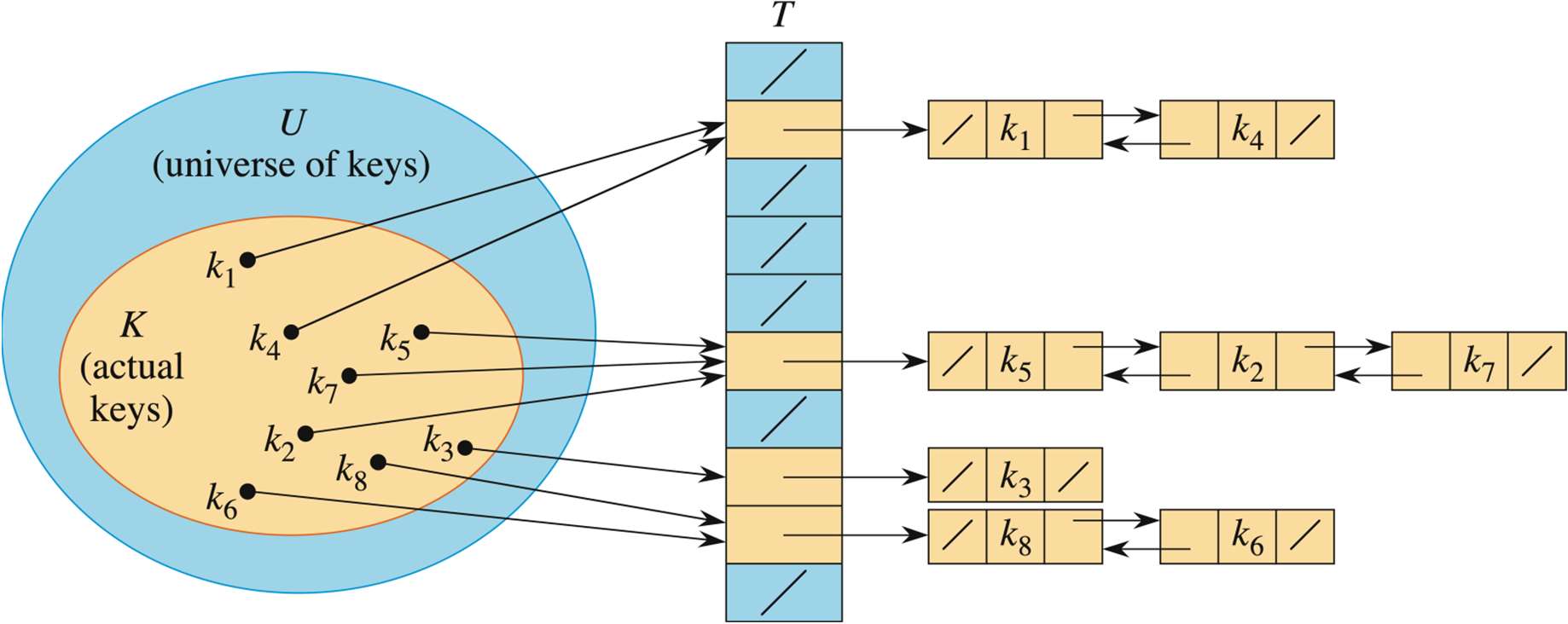
此时有两个定理去证明了链接法能让查找的时间复杂度为 :
- 在独立均匀散列的前提下,在一个使用链地址法解决冲突的散列表中,一次 不成功 的查找的平均时间为 。
- 在独立均匀散列的前提下,在一个使用链地址法解决冲突的散列表中,一次 成功 的查找的平均时间为 。
这两个定理的证明不是重点,这里就跳过了。
开放寻址法
对于开放寻址法,之前的文章也提到了很多。开放寻址法的优点:避免了指针的聚集,而且由于可以直接存储关键字,不需要存储指针,节约了存储空间,这些存储空间可以用来构造更多的槽位,进而减少了冲突,加速了查找。
对于每个关键字k,使用开放寻址法的探查/探测序列(probe sequence),我们有如下操作:
- HASH-INSERT:默认插入散列表中不存在的关键字,如果散列表已满则报错。
- HASH-SEARCH:按照探测序列查找目标关键字,如果不存在则返回NUL。
HASH-INSERT(T, k) i = 0 repeat q = h(k, i) if T(q) == NIL T[q] = k return q else i = i + 1 until i == m error "hash table overflow"
HASH-SEARCH(T, k) i = 0 repeat q = h(k, i) if T[q] == k return q i = i + 1 until T[q] == NIL or i == m return NIL对于删除操作,开放寻址法的删除比较麻烦。当我们从某槽位删除关键字时,不能简单地将槽位设置为NUL,如果这样做,就会出现问题。所以需要为该槽位增加 DELETED 标记,同时对 HASH-INSERT 进行修改。但是这样做的结果是查找时间不再依赖于装填因子 α ,因此针对必须需要进行删除操作的散列表,一般更多的是采用链地址法。
开放寻址法中,寻址策略根据之前文章中提到的,一般有: 线性探测法(linear probing)、双散列法(Double hashing) 以及 完全散列(perfect hashing)。
我们一般使用双散列比较多,下面是一个使用双散列的例子:
Consider inserting the keys
10, 22, 31, 4, 15, 28, 17, 88, 59into a hash table of lengthm = 11using open addressing. Illustrate the result of inserting these keys using double hashing withh1(k) = k mod mandh2(k) = 1 + (k mod (m - 1)).
我们整合一下上面的两个函数,可以得到函数h(k,i),k表示关键字, i从0开始 ,表示初始位置的基础上进行偏移的度:
h(k, i) = (h1(k) + i*h2(k)) mod m
= (k mod m + i(1 + (k mod (m - 1)))) mod m
那么我们可以列一个表来表示:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | ||||||||||
| 22 | 10 | |||||||||
| 22 | 31 | 10 | ||||||||
| 22 | 4 | 31 | 10 | |||||||
| 22 | 4 | 15 | 31 | 10 | ||||||
| 22 | 4 | 15 | 28 | 31 | 10 | |||||
| 22 | 17 | 4 | 15 | 28 | 31 | 10 | ||||
| 22 | 17 | 4 | 15 | 28 | 88 | 31 | 10 | |||
| 22 | 59 | 17 | 4 | 15 | 28 | 88 | 31 | 10 |
其中,有如下冲突:
- 15插入时,冲突偏移i = 2;
- 17插入时,冲突偏移i = 1;
- 88插入时,冲突偏移i = 2;
- 59插入时,冲突偏移i = 2;
整个过程还是比较简单的,但对于分析还是有些困难:
我们有如下定理用于证明:
假设采用独立均匀排列散列,给定一个装填因子 的开放寻址散列表,则查找不成功的探测次数的期望至多为 。此时在运用开放寻址法的散列表中,关键字个数 。
定理在此就不做证明了。

