
前言
好久没有更新,最近忙于复习周前的各种quiz和ddl,终于到了复习周可以好好复习更新了。这一章是关于线性时间内的排序的算法分析。
比较排序的下界证明
首先我们知道, 决策树(decision tree): 是一棵 满二叉树(full binary tree) (每个结点要不没有孩子结点,要不有两个孩子结点),用来表示对给定规模的输入序列执行特定的排序算法过程中的元素比较。例如下面是一个比较三个元素的决策树:
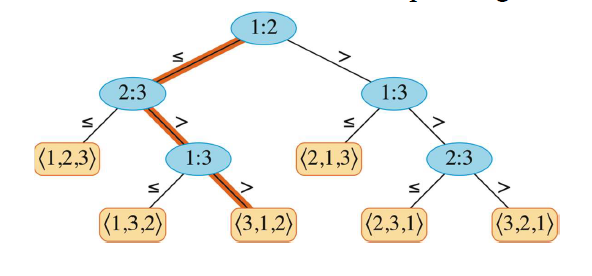
接着我们回顾之前的比较排序算法,它们最低的时间复杂度也需要 ,下面是证明:
设决策树高度为h,叶结点个数为l,此时可以知道 因为如上图所示,h高度为从决策树根结点到可达叶结点的最长简单路径的长度。对于n个变量的问题,这n个变量有n!种可能的顺序(如上图3个变量排序,有3! = 6种可能)。因此, 。根据Sterling 近似公式,有 带入可得,
计数排序
计数排序的思想非常简单,对于一个数组A[1
- 遍历数组A,统计A中当前数据出现的次数,并且该数据作为索引,出现次数存在C中。
- 从0开始,累加数组C( ),用于定位该数据在输出中的最后位置。
- 反向遍历A,查找A[j]数据在C中的数据,它记录着A[j]数据的最后位置,并在B中的对应位置(对应C中存的地址数据)放上数据A[j],接下来C[A[j]]—,继续遍历A的下一位直到结束。
- 输出B为答案。
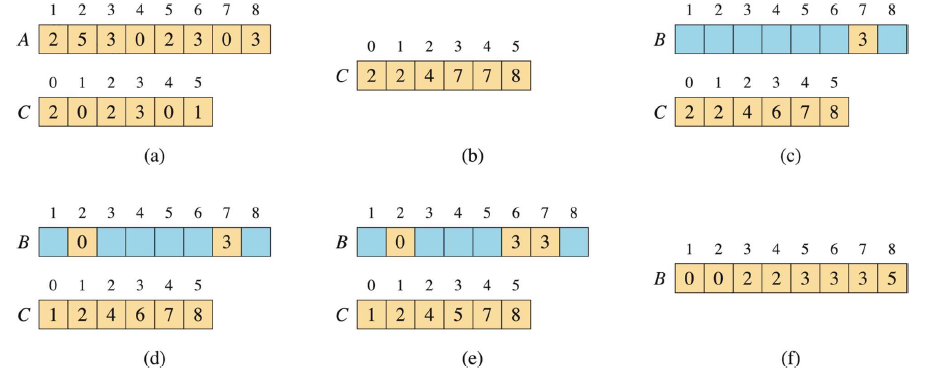
COUNTING-SORT(A, n, k) let B[1:n], C[0:k] be new arrays for i = 0 to k C[i] = 0 for j = 1 to n C[A[j]] = C[A[j]] + 1 // C[i] now contains the number of elements equal to i. for i = 1 to k C[i] = C[i] + C[i - 1] // C[i] now contains the number of elements less than or equal to i. // Copy A to B, starting from the end of A for j = n downto 1 B[C[A[j]]] = A[j] C[A[j]] = C[A[j]] - 1 // to handle duplicate values举例说明:例如A[NUL,2,5,3,0,2,3,0,3] (从1开始,第0为未知设置为NUL),则按照上面的步骤:
- C的大小为[0:5],因为5为数据中最大的数,C的统计初始值为:[2,0,2,3,0,1],如图中(a)
- 遍历并累加数组C,确定数据A[i]在输出B中的最后位置,累加后C的值为:[2,2,4,7,7,8]。这里演示一小部分:
- C[1] += C[0] = 2,此时数据1在输出中的最后地址为2,但是与数据0相同,所以数据1不存在。
- C[2] +=C[1] = 4,此时数据2在输出中的最后地址为4,此时相当于从上一个地址开始,有2位是数据2的。
- 以此类推,如图中(b)…
- 反向遍历A,查找A[j]数据在B的最后位置(存于C[A[j]]中),并给那个位置放上数据A[j]。从尾部开始,先是数据3,找到C[3]的最后位置为7,那么第一个3就被放到第7位上(B与A一样从1开始),同时C[3]—得6(如图(c))。接下来到数据0,找到C[0]的最后位置为2,把一个0放到B的第2位上,同时C[0]— = 1(如图(d))。依次类推(如图(e))……
- 最后得到B为[0,0,2,2,3,3,3,5](如图(f))
综上所述,计数排序适用于对一个数组中存在重复元素的情况进行排序,很明显,它的时间复杂度为 。对于计数排序中,我们C中存的是该数据的最末地址,而我们也是从末位开始遍历原数组A,故同数据的排序前后顺序不变,是个稳定的(stable)排序。
对于稳定性,这里需要拓展一个概念——卫星数据(Satellite Data),它是除了需要排序的主要关键字之外的其他关联数据。例如:一个结构Stu中,有两个属性:id和score,学生1的数据为s1.id = 001, s1.score = 99; 学生2的数据为s2.id = 002, s2.score = 99. 设score为需要排序的关键字,那么此时id就是卫星数据。
对于讨论一个排序算法的稳定性,它要求如果两个记录有相同的主键,则它们在排序后的顺序仍与排序前的顺序一致。即要求, 它们排序之后卫星数据的顺序不变 。
此外,我们已经学习过的具有稳定性的排序有 插入排序,冒泡排序,归并排序等 。
我们知道上述代码中,我们新建了一个B数组,会使得空间复杂度变为O(n),如果设由n个元素组成的输入序列每个元素都是区间[0
COUNTING-SORT(A, n, k) let C[0:k] be new arrays for i = 0 to k C[i] = 0 for j = 1 to n C[A[j]] = C[A[j]] + 1 // C[i] now contains the number of elements equal to i. p = 1 for i = 0 to k while C[i] > 0 A[p] = i p = p + 1 C[i] = C[i] - 1此时修改的部分有:
- 第二步此时C记录的是数据A[j]在输出时的 最初位置(故C[A[j]] + 1)。
- 输出的时候 需要从头遍历数组 ,因为此时为最初位置。用一个变量p记录输出到A中的索引值。
基数排序
对于基数排序,是将数据按照基数的顺序(0~9,x mod 10得到的)进行排序,再对基数内的数据进行排序的算法。实际上可以看成是桶排序的一种情况,这里就不过多讨论了,详情请见之后的桶排序和之前对于基数排序的介绍:
https://hoyue.fun/data_structure_hmk2.html#i-3
桶排序
我们通过假设输入数据以分析桶排序。假设一组数据总体为X,X~U(0,1),表示数据在区间[0,1)上满足均匀分布。桶排序将区间[0,1)分成n个大小相等的子区间,称这些子区间为 桶(bucket) 。
那么我们就设数据数组A[1
那么桶排序的步骤为:
- 根据A数组新建B链表数组,并初始化为0。
- 将A数组中的元素依次按照一定的规则插入到桶中。(有点像散列表)。
- 对每个桶内部进行插入排序,当插入排序规模很小的时候,趋向于 。
- 按顺序输出每个桶(桶设置时是有序的)。
对于上述这样的数据,我们可以写出这样的代码:
BUCKET-SORT(A, n) let B[0 : n - 1] be a new array for i = 0 to n - 1 make B[i] an empty list for i = 1 to n insert A[i] into list B[⌊n · A[i]⌋] for i = 0 to n - 1 sort list B[i] with insertion sort concatenate the lists B[0], B[1], ... , B[n - 1] together in order return the concatenated lists举个例子,下述数据 A[0.78,0.17,0.39,0.26,0.72,0.94,0.21,0.12,0.23,0.68](如图中(a)),将被分成10个桶,每个桶的映射方式是 10 * A[i] 并取整。将它们插入桶中后,对每个桶进行小规模插入排序后如图中(b),最后输出桶数据即有序的。
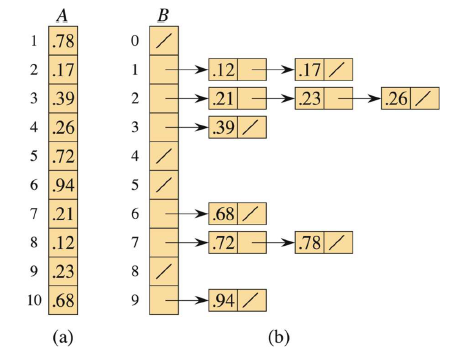
这个过程是非常清晰易懂的,但是分析其时间复杂度却没有这么简单。
在最坏的情况下(所有的数据都插到同一个桶中),我们发现除了插入排序外,其他的均为 。因为插入排序的时间代价为平方阶的,那么整体的桶排序时间代价为:
我们计算平均的运行时间,对这个式子取数学期望(mean):
因为根据概率统计知识,我们知道一共有n个桶,这个数据落入这个桶的概率为1/n,数据落入桶这个过程它满足二项分布 ,(此时因为对于每个数据进入桶这个事件,提供的数据是离散的,采用离散概率分布二项分布,而不是均匀分布)那么此时它的:
- ;
- ;
- ;
所以继续化简:
综上所述,我们可以知道,即使输入数据不服从均匀分布,桶排序也仍然可以在线性时间内完成。只要输入数据满足所有桶大小的平方和与总的元素个数呈线性关系(即 为线性)。
当然, 在最坏的情况下所有的数据都插到同一个桶中 , ,因为插入排序最差的情况即为 。
我们可以修改插入排序为归并排序或者堆排序。 这样保证平均情况运行时间为线性的同时,最坏情况下运行时间为

