
前言
近期临近考试,这里就对栈和队列中重要应用——十进制转二进制(栈)、队列链表实现和斐波那契数列以及最大公因数的算法,写一篇单独的集合,就当做是练习和复习了。
之前栈和队列的,已经包含在链表部分里了:
https://hoyue.fun/data_structure_2.html
十进制转二进制
十进制转二进制的方法除了把十进制分成2的幂的和以外,在比较小的情况下还可以使用短除法。使用短除法转换出的二进制需要逆序输出,例如:
2⌊13 1
2⌊6 0
2⌊3 1
2⌊1 1
逆序输出:
此时发现,我们先得到的余数后出来,很符合栈的存储原理,故我们可以把输出结果压入栈中存储。
这个算法就是一个非常简单的栈的实现,故这里就只展示部分函数:
typedef struct dectobina_stack{ struct dectobina_stack* next; int d;}stack;
stack* create(void) //创建一个哑节点{ stack *s=(stack *)malloc(sizeof(stack)); if(s == NULL) { printf("No Space!\n"); return NULL; } s->next=NULL; return s;}
stack* push(stack *s, int data) //从头push入{ stack *node=(stack *)malloc(sizeof(stack)); if(node == NULL) { printf("No Space!\n"); return NULL; } node->d=data; node->next=s->next; //连接原来的头结点 s->next=node; //成为头结点 return s;}
int pop(stack *s){ if(s->next != NULL) { int data=s->next->d; stack *p=s->next; //储存当前头结点 s->next=s->next->next; //头结点移动到下一位 free(p); //释放原来的头结点p return data; } else return -1;}
void DisposeStack(stack *s) //删除栈{ if(s!=NULL) { stack *p=s; while(p) { stack *q=p->next; //记录下一位,防止释放后找不到 free(p); p=q; } }}下面是一个简单的测试程序:
#include "stack.h"#include<stdio.h>#include<stdlib.h>
int main(){ int n; printf("Please input a decimal number.\n"); scanf("%d",&n); stack *s=create(); for(;;) { int rem=n%2; //取余 int div=n/2; //去尾 push(s,rem); //把余数push if(div) //如果没除完继续短除 n=div; else break; } for(;;) { if(s->next != NULL) //如果栈中还有数据 printf("%d",pop(s)); else break; } DisposeStack(s);}队列的链表实现
队列的ADT在链表中的实现是一个非常常用,而且常考的考点。队列用链表实现,还需要在链表上满足队列先进后出的特点——在链表的头部出列,在链表的尾部入列。
而与传统链表不同的是,由于队列的特征,我们会很经常用到头结点和尾结点,重复查询头尾节点会浪费很多时间,我们一般另外使用一个结构体来记录当前队列的头指针和尾指针,可能还会有记录队列的长度什么的。
我们使用两个结构体,一个存储队列的结点内容,一个存储这个队列首位信息和队列长度:
typedef int ElementType;typedef struct node{ ElementType data; struct node* next;}QUEUE_NODE;typedef struct QueueRecord{ QUEUE_NODE* front; QUEUE_NODE* rear; int count;}*Queue,queue;接下来是队列的一些参考函数:
- CreateQueue:创建一个空队列,并且初始化它。返回为新创建的队列的地址。
- IsEmpty:判断当前队列是否为空,即判断首指针是否为空。
- Enqueue:入队,即在队尾插入一个新数据,并更新队列尾指针。
- Dequeue:出队,即队首元素出队,并更新首指针。
- Front:找到队首元素,并返回。
- FrontAndDequeue:返回队首元素,并将其出队。
- MakeEmpty:清空队列。
- DisposeQueue:摧毁队列。
- PrintQueue:输出队列。
故代码为:
#include "QueueLinked.h"#include<stdio.h>#include<stdlib.h>
Queue CreateQueue(void) //创建的是空队列,其中没包含任何队列节点{ Queue q=(Queue)malloc(sizeof(queue)); if(q == NULL) { printf("No Space!\n"); return NULL; } q->count=0; q->front=NULL; q->rear=NULL; return q;}
int IsEmpty(Queue Q) //判断队列首指针是否存在{ return (!Q->front)?1:0;}
void Enqueue(ElementType X, Queue Q){ Q->count++; QUEUE_NODE* p=(QUEUE_NODE *)malloc(sizeof(QUEUE_NODE)); if(p == NULL) { printf("No Space!\n"); exit(-1); } p->data=X; p->next=NULL; if(IsEmpty(Q)) //此时如果原本就不存在任何队列节点,则新创建的这个节点将为首尾地址 { Q->front=p; Q->rear=p; } else { Q->rear->next=p; Q->rear=p; }}
void Dequeue(Queue Q){ if(!IsEmpty(Q)) { QUEUE_NODE *p=Q->front->next; free(Q->front); Q->front=p; if(IsEmpty(Q)) //如果只剩下一个节点,出队后首尾都为空 Q->rear=NULL; Q->count--; }}
ElementType Front(Queue Q){ if(!IsEmpty(Q)) return Q->front->data; else return -1;}
ElementType FrontAndDequeue(Queue Q){ ElementType d; if(!IsEmpty(Q)) { d=Q->front->data; Dequeue(Q); } return d;}
void MakeEmpty(Queue Q){ while(!IsEmpty(Q)) { Dequeue(Q); }}
void DisposeQueue(Queue Q){ for(QUEUE_NODE* i=Q->front;!i;) //从首位置遍历到尾位置 { QUEUE_NODE* p=i->next; free(i); i=p; }}
void PrintQueue(Queue Q){ printf("There is a %d-size queue:\n",Q->count); QUEUE_NODE* p=Q->front; while(p) { printf("%d ",p->data); p=p->next; }}队列ADT的实现还是比较简单的,之后优先队列(堆)将涉及更多。
斐波那契数列
斐波那契数列是递归中一个非常经典的例题,但它在递归中并不高效。
斐波那契数列是这样的一串数:1、1、2、3、5、8、13、21、34…
斐波那契数列函数F(x)满足:F(0)=1, F(1)=1,When N>1,F(N)=F(N-1)+F(N-2);
我们由递推式很容易就可以看出可以使用它可以通过递归来实现:
int Fibonacci1(int N){ if(N<=1) return 1; else return Fibonacci1(N-1)+Fibonacci1(N-2);}但是它是一个类似指数增长的过程,我们列出1~6次的求解:
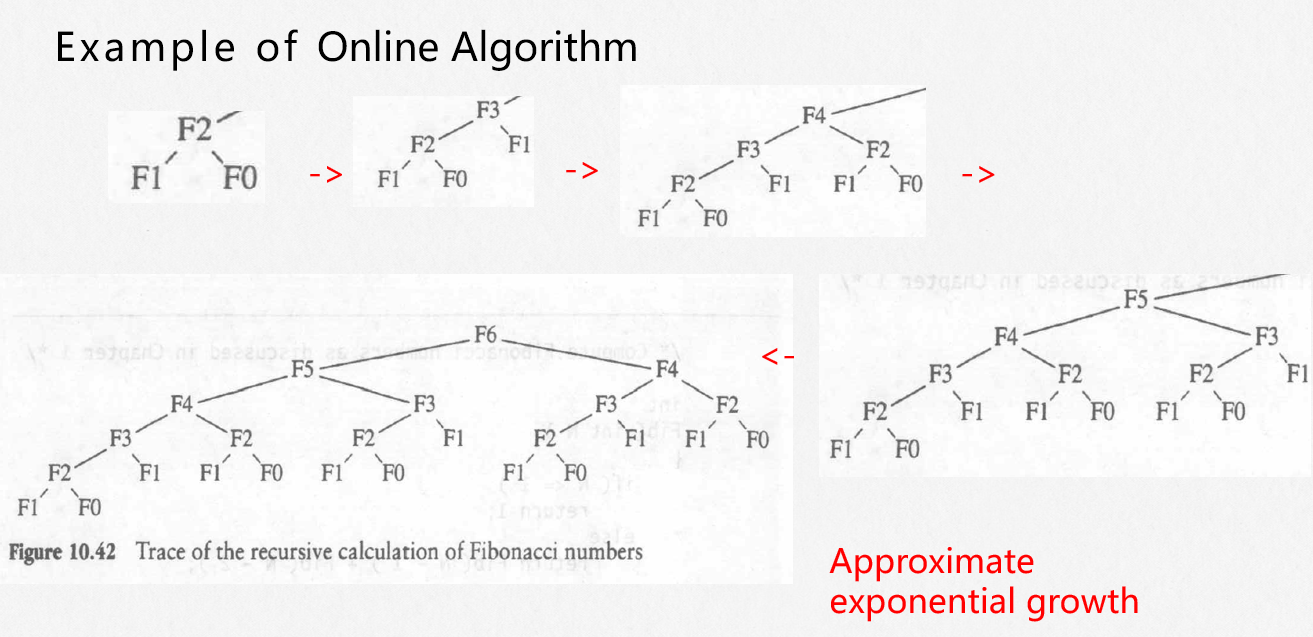
可以发现在递归中我们重复计算了很多次相同的,导致效率低下。
我们发现,想要找到F(n)的值只与F(n-1)和F(n-2)有关,而要解决重复计算的问题,只需要我们记录好F(n-1)和F(n-2)的值,就可以找到F(n)的值,并且动态替换F(n-1)和F(n-2),就能找到任何一位的值了。
所以我们把递归改造为循环来实现:
int Fibonacci2(int N){ if(N<=1) return 1; int Last=1, NextToLast=1, ans; /* Last用于记录F(N-1),NextToLast记录F(N-2),ans记录当前的F(N) */ for(int i=2;i<N;i++) { ans = Last + NextToLast; //F(N)=F(N-1)+F(N-2) NextToLast = Last; Last = ans; /* 动态移动Last和NextToLast的值 */ } return ans;}这样时间复杂度就降到了 ,效率就会比递归的高。
我们把这样存在递推式的情况称为递推。递推与递归不一样,要看情况来选择。
欧几里得算法(辗转相除法)
欧几里得算法又称辗转相除法,是用于计算两个非负整数a,b的最大公约数的算法。
它依靠定理: 两个整数的最大公约数等于其中较小的那个数 和 两数相除余数 的最大公约数。
举个例子:
假如需要求 1997 和 615 两个正整数的最大公约数,用欧几里德算法,是这样进行的:
1997 / 615 = 3 (余 152) 615 / 152 = 4(余7) 152 / 7 = 21(余5) 7 / 5 = 1 (余2) 5 / 2 = 2 (余1) 2 / 1 = 2 (余0)
至此,最大公约数为1 以除数和余数反复做除法运算,当余数为 0 时,取当前算式除数为最大公约数,所以就得出了 1997 和 615 的最大公约数 1
我们可以发现,欧几里得算法中,每次被除数会变成上一次除法的除数,而除数则会变成上一次除法的余数。当余数为0时结束,我们把这个算法写成函数的形式:

注意要让a mod b,一般都会要求a>b才能进行。所以传入时一般需要确保a>b。
它就很满足递归的情况,故可以使用递归来写:
int gcd1(int m,int n){ if(n == 0) return m; else return gcd1(n,m%n); //使用尾递归防止空间浪费}当然我们也可以直接使用循环来实现:
int gcd2(int m,int n){ while(n > 0) { int rem = m % n; //表示余数 m = n; n = rem; } return m;}后记
对于使用链表的题目,对于链表的操作,建议画一个简易链表图,更加容易看出该如何操作。
而对于递归的,一定是当子问题和问题一模一样或非常相似,且必须有递归停止条件,防止死递归。如果可以的话,使用尾递归会使效率提高。
当然对比递推和递归,能使用递推的一般效率都会比递归要高很多。而大部分递归都可以使用循环代替,循环一般也比递归效率要高,但递归也有其特别的实现,还需要具体看题目情况。

