2567 字
13 分钟
【数据结构】作业二——栈与树
2022-11-22
2024-01-13
学习笔记/数据结构
作业
/
排序
/
数据结构

文章目录

前言
逆序输出
基数排序
实现
找到轮次
取出某个数的某一位
创建桶
插入桶以及提出至数组
最终代码
平衡符号
递归
统计树叶
AVL双旋转改进
RL
LR
参考

前言#

这一篇是第二次的作业，因为在期中考试的时期，近期略有忙碌没时间做这个作业，故在ddl之前才写上来。这一篇包含了作业中的一小部分，逆序输出、基数排序、平衡符号、一些简单的递归、AVL双旋转改进等。

逆序输出#

这一道题目主要用于练习使用链表存储数据、处理数据。

完成逆序输出，如果输入为0,1,2,3,4,5,6,7,8,9，则输出9,8,7,6,5,4,3,2,1。不能使用数组与下标形式，只能使用单向链表实现。

做到这个我们一般可以有以下的思路：

  • 每一位交换位置。
  • 逆序输入，即在头部插入，即做成一个栈。
  • …

每一位的交换因为要求使用的是单向链表，不是很方便，而新建一个链表头部插入则简单不少。故代码为：

List reverse(List L)
{
    if(IsEmpty(L))    //判断是否为空
        return NULL;
    List G=(List)malloc(sizeof(struct Node));
    G->Next=NULL;
    PtrToNode p=L->Next;
    while(p)
    {
        Insert(p->Element,G,G);
        //插入元素为p->Element，链表为G，插在G的后面，即插在了头部
        p=p->Next;
    }
    DeleteList(L);    //删除之前的链表
    return G;
}

基数排序#

基数排序 （英语：Radix sort）又称”桶排序”（bucket sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。

实现方法：

  1. 将所有待比较数值 统一为同样的数位长度 ，数位较短的数 前面补零
  2. 然后从最低位开始，依次进行一次排序
  3. 这样从最低位排序一直到最高位排序完成以后，序列就变成了一个有序序列

我们来看一个图解来了解这个算法会比较简单：

一步一步来，假设我们最大的数最大位数为3位，即百位。数列为：{53,3,54,748,14,214}

第一轮：比较 个位数

  1. 将每个元素的 个位数 取出，然后放到对应的桶（代表着各个基数）中（桶为一个一维数组）。
  2. 按照这个桶的顺序，依次取出数据，放回原来的数组。

注意，这里的依次为：从小的基数到大的基数，同基数内 先进先出（类似队列） 。

接下来同理是第二轮：比较 十位数 。

第三轮：比较 百位数。

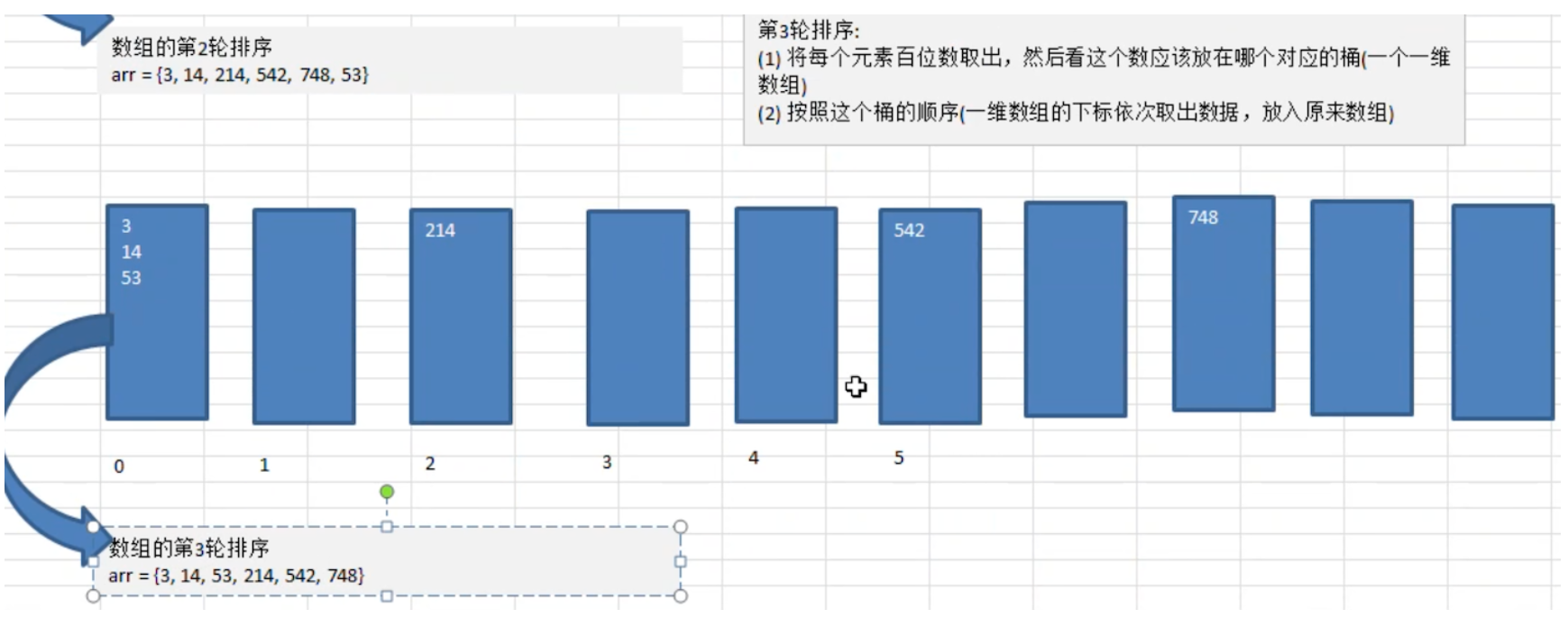
这样就结束了，我们找到了一个新的序列。

我们分析这个过程，我们需要做的分成几个操作来分析：

实现#

找到轮次#

我们的轮次是由数组中最大的数的位数决定的，故我们需要先遍历一次找到最大的数，再取其最大位数。

int findmaxe(int *arr)
{
    int maxima=-1;
    while(*arr)    //找到数组中最大值
    {
        maxima=(*arr > maxima)?*arr:maxima;
        arr++;
    }
    int maxe=1;    //找到最大值的位数
    while(maxima/10)    //如果不是最后一位，则/10
    {
        maxima/=10;
        maxe++;
    }
    return maxe;
}

取出某个数的某一位#

我们取出一个数的最后一位是对这个数%10（除10取余），我们只需要把要取出的那一位变成最后一位，%10即可。变成最后一位，即小数点向左移动到那一位。

int GetDigit(int x, int y)    //取x的第y位（个位从0开始数）
{
    int i, t = 1;
    for(i=0; i<y; i++)
        t*=10;
    return (x/t)%10;
}

创建桶#

我们用一个链表表示一个桶，那么基数有10个（0-9），则需要10个桶，于是需要创建的是，代表10个链表的指针数组。并且我们将其初始化：

List bucket[10];
for(int i=0; i<10; i++)
    bucket[i]=CreateList();

其中的CreateList：

PtrToNode CreateList(void)
{
    PtrToNode p = (struct Node*)malloc(sizeof(struct Node));
    p->Next = NULL;
    return p;
}

在每一轮开始前，我们都需要把桶清空：

for(int j=0; j<10; j++)
    MakeEmpty(bucket[j]);

其中MakeEmpty函数：

void MakeEmpty(List L)
{
    Position p, tmp;
    p = L->Next;
    while(p != NULL)
    {
        tmp = p->Next;
        free(p);
        p = NULL;
        p = tmp;
    }
    L->Next = NULL;
}

插入桶以及提出至数组#

接下来就是调用之前的取出某个数的某一位的函数，并且将其插入桶中。因为这个插入符合先进先出的情况，故可以使用队列来代替这些普通的链表。插入在队尾处插入：

void InsertBack(ElementType X, List L)
{
    Position pos;
    PtrToNode pNode;
    // move to tail
    pos = L;
    while(pos->Next != NULL)    //pos最后为最后一项
        pos = pos->Next;
    pNode = (struct Node*)malloc(sizeof(struct Node));
    pNode->Element = X;
    pNode->Next = NULL;
    pos->Next = pNode;
}

最后结果存回arr数组中。即从各个链表中提取数据，我们把各个链表从头部出链表即可。

最终代码#

最终这个排序程序可以组装成下面代码的集合。 以上代码部分参数可能和下方不同，可能需要修改。

首先是单向链表的实现函数们，我这里就直接使用课本中的实现了。下面是主函数部分：

#include <stdio.h>
#include <stdlib.h>
#include "list.h"


#define N 10    // 排序的数个数


void RadixSort(int arr[]);
int GetDigit(int x, int y);
void PrintArray(int arr[], int size);
PtrToNode CreateList(void);
void  InsertBack(ElementType X, List L);
int findmaxe(int *arr);


int main()
{
    int i;
    int arr[N] = {64, 8, 216, 512, 27, 729, 0, 1, 343, 125};
    printf("before sort: ");
    PrintArray(arr, N);
    RadixSort(arr);
    printf("after sort: ");
    PrintArray(arr, N);
    return 0;
}


void RadixSort(int arr[])
{
    List bucket[10];
    int P=findmaxe(arr);
    // 创建桶
    for(int i=0; i<10; ++i)
        bucket[i]=CreateList();      // 从低位到高位循环每一位数字
    for(int i=0; i<P; ++i)
    {
        // 将桶置空
        for(int j=0; j<10; ++j)
            bucket[j]=MakeEmpty(bucket[j]);  // 根据当前位上的数字，将之放入对应桶中。并注意顺序（后进的放在后面）
        for(int j=0; j<N; ++j)
        {
            int digit = GetDigit(arr[j], i);
            InsertBack(arr[j], bucket[digit]);
        }
        int k = 0;
        // 将每趟排序后的结果存回arr
        for(int j=0; j<10; j++) { Position pos = First(bucket[j]); while(pos != NULL) { arr[k++] = pos->Element;
                pos = pos->Next;
            }
        }
    }
    for(int i=0; i<10; ++i)
        DeleteList(bucket[i]);
}




// 取整数x的倒数第y位数字，y从0开始
int GetDigit(int x, int y)    //取x的第y位（个位从0开始数）
{
    int i, t = 1;
    for(i=0; i<y; i++)
        t*=10;
    return (x/t)%10;
}


void PrintArray(int arr[], int size)
{
    int i;
    for(i=0; i<size; ++i) { printf("%d ", arr[i]); } printf("\n"); } int findmaxe(int *arr) { int maxima=-1; while(*arr) //找到数组中最大值 { maxima=(*arr > maxima)?*arr:maxima;
        arr++;
    }
    int maxe=1;    //找到最大值的位数
    while(maxima/10)    //如果不是最后一位，则/10
    {
        maxima/=10;
        maxe++;
    }
    return maxe;
}


PtrToNode CreateList(void)
{
    PtrToNode p = (struct Node*)malloc(sizeof(struct Node));
    p->Next = NULL;
    return p;
}


void InsertBack(ElementType X, List L)
{
    Position pos;
    PtrToNode pNode;
    // move to tail
    pos = L;
    while(pos->Next != NULL)
        pos = pos->Next;
    pNode = (struct Node*)malloc(sizeof(struct Node));
    pNode->Element = X;
    pNode->Next = pos->Next;
    pos->Next = pNode;
}

（*参考代码来源位于文章底部）

平衡符号#

这一题是栈的经典题目，之前在栈那一章也有提到，这里就重新写一下。

给定一个只包括 ’(’，’)’，’{’，’}’，’[’，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。
  3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = ”()” 输出：true

示例2：

输入：s = ”()[]{}” 输出：true

示例3：

输入：s = ”(]” 输出：false

思路也比较明显——我们可以遇到左括号时压入栈中，遇到右括号中出栈，判断当前符号是否匹配就可以了。注意还有两种情况，一是该出栈时栈为空，此时左括号没有了，右括号还有，不平衡；二是到了读取完所有的符号，栈还不为空，此时左括号还有右括号没有了，不平衡。

int vavid(char *arr)
{
    Stack S=CreateStack();
    while(*arr)
    {
        if(*arr == '(' || *arr == '[' || *arr == '{')    //左括号入栈
            Push(*arr,S);
        else    //右括号出栈
        {
            if(IsEmpty(S))    //特殊情况1
                return 0;
            else
            {
                char t=Top(S);
                Pop(S);
                if(!((t == '(' && *arr == ')') || (t == '[' && *arr == ']') || (t == '{' && *arr == '}')))
                    return 0;
            }
        }
        arr++;
    }
    if(IsEmpty(S))    //特殊情况2
        return 1;
    else return 0;
}

递归#

题目中还有一些简单的递归，例如阿克曼函数：

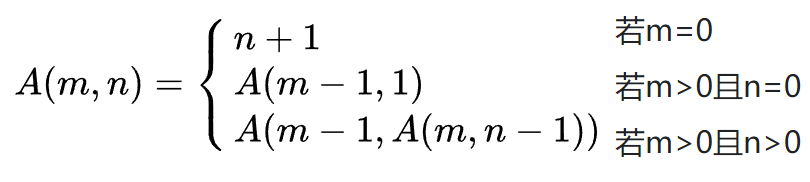
这个就是个非常明显的递归，我们直接根据它的条件写就行。

int Ackerman(int m,int n)
{
    if(m == 0)
        return n+1;
    else if(m>0 && n==0)
        return Ackerman(m-1,n);
    else if(m>0 && n>0)
        return Ackerman(m-1,Ackerman(m,n-1));
}

统计树叶#

使用递归来实现统计树的树叶节点个数。

那这道题目就在于如何递归，统计树叶节点，就是该节点左右孩子均为NULL，遇到这样的节点返回1就行，在递归时把左边的树叶数和右边的树叶数相加就行。

int leaf(BTNode *t)
{
    if(t == NULL)    //结束递归，回溯
        return 0;
    else if(!t->Left && !t->Right)    //找到树叶
        return 1;
    else
        return leaf(t->Left) + leaf(t->Right);    //左树叶数加右树叶数
}

其中树的一些实现函数如下：

typedef int ElementType;
typedef struct BTreeNode
{
    ElementType Element;
    struct BTreeNode*  Left;
    struct BTreeNode*  Right;
}BTNode;


int leaf(BTNode *t);
BTNode* Insert(BTNode *T, ElementType d);
void PrintTree(BTNode *T);
BTNode *Insert(BTNode *T, ElementType d)
{
    if(T == NULL)
    {
        T=(BTNode *)malloc(sizeof(BTNode));
        if(T == NULL)
        {
            printf("Error, no space!\n");
            exit(-1);
        }
        T->Element=d;
        T->Left=NULL;
        T->Right=NULL;
        return T;
    }
    else if(d < T->Element)
    {
        T->Left=Insert(T->Left,d);
    }
    else if(d > T->Element)
    {
        T->Right=Insert(T->Right,d);
    }
    else if(d == T->Element)
    {
        printf("Error, %d exited.\n",d);
    }
}


void PrintTree(BTNode *T)
{
    if(T != NULL)
    {
        printf("%d ",T->Element);
        PrintTree(T->Left);
        PrintTree(T->Right);
    }


}

AVL双旋转改进#

我们知道AVL双旋转是调用了两次单旋转完成的，但这样会造成一定的浪费，我们可以对它进行改进，让它一步到位。

关于旋转，我们都可以通过旋转图来实现：

RL#

对于RL旋转，我们只看最左边的初始树和最右边的旋转结果树。我们要做的就是四步：

  1. k1的右孩子变为k2的左孩子，
  2. k3的左孩子变为k2的右孩子，
  3. k2的左孩子变为k1，
  4. k2的右孩子变为k2。

就可以做到直接的双旋转了，故我们看着这张图，代码为：

AvlTree left_right_rotation(AvlTree k3)
{
    AvlTree k1=k3->Left;    //找到k1先
    AvlTree k2=k1->Right;    //找到k2
    //执行四步
    k1->Right=k2->Left;
    k3->Left=k2->Right;
    k2->Left=k1;
    k2->Right=k3;
    return k2;
}

看着图来写还是比较简单的。

LR#

同理对于LR，我们看图可知四个步骤：

  1. k1的右孩子变为k2的左孩子，
  2. k3的左孩子变为k2的右孩子，
  3. k2的左孩子变为k1，
  4. k2的右孩子变为k2。

我们可以发现，它们其实做的操作是一样的，只有k1,k2,k3的原始位置不同而已！

故代码为：

AvlTree right_left_rotation(AvlTree k1)
{
    AvlTree k3=k1->Right;
    AvlTree k2=k3->Left;
    k1->Right=k2->Left;
    k3->Left=k2->Right;
    k2->Left=k1;
    k2->Right=k3;
    return k2;
}

参考#

【数据结构】作业二——栈与树
https://hoyue.fun/data_structure_hmk2.html
作者
Hoyue
发布于
2022-11-22
最后更新于
2024-01-13
许可协议
CC BY-NC-SA 4.0
评论
【数据结构】树 ——AVL树
乌鸦 喜鹊
Copyright © 2025 Hoyue. All Rights Reserved.
RSS / Sitemap
Powered by Astro & Fuwari
tencet 萌ICP备20210332号