堆属性#

二叉堆(binary heap) 可以用数组表示，这个数组对应一棵完全二叉树。根据层序遍历顺序对完全二叉树结点进行编号，其中根结点下标为 1 。

堆可以存储在数组(A)中，那么其他的属性我们可以很容易得到：

• 节点高度= 从节点到叶子的最长简单路径上的边数。
• 堆的高度= 根的高度= $\Theta(\lfloor \lg n \rfloor)$ 。
• 树的根(root)是A[1]。
• A[i]的父母(parent)节点= $A[\lfloor i/2 \rfloor]$ ，向下取整。
• A[i]的左孩子(left child)= $A[2i]$ 。
• A[i]的右孩子(right child)= $A[2i + 1]$ 。
• A.heap-size表示A中存储了多少元素。只有 $A[1: A.heap-size]$ 在堆中。
• 对于max-heaps（根上为最大元素）：对于除根之外的所有节点i， $A[PARENT(i)] \geq A[i]$ 。
• 对于min-heaps（根上为最小元素）：对于除根之外的所有节点i， $A[PARENT(i)] \leq A[i]$ 。

我们把父母节点与孩子用函数表示：

1
PARENT(i)
2
    return ⌊i/2⌋
3
LEFT(i)
4
    return 2i
5
RIGHT(i)
6
    return 2i + 1

维护堆#

我们要检查数组A下标i的元素，是否符合堆的性质，我们需要根据堆的性质，将其调整到合理的位置。

在堆中下标i的元素发生变化的时，我们要对堆进行维护，将其重新调整为一个堆，使得堆的性质不变。

以大根堆为例，我们使用下面函数来维护堆：

1
MAX-HEAPIFY(A, i)
2
    l = LEFT(i)
3
    r = RIGHT(i)
4
    if l ≤ A.heap-size and A[l] > A[i]
5
        largest = l
6
    else largest = i
7
    if r ≤ A.heap-size and A[r] > A[largest]
8
        largest = r
9
    if largest ≠ i
10
        exchange A[i] with A[largest]
11
        MAX-HEAPIFY(A, largest)

这个过程是一个向下调整（Percolate Down）的过程，将A[i]和其左右孩子进行比对，如果不是三者中最大的，就说明不符合大根堆性质，该结点和三个结点中最大的结点进行交换，递归执行。

例如下面这个例子，维护 位置2结点值为4 的结点：

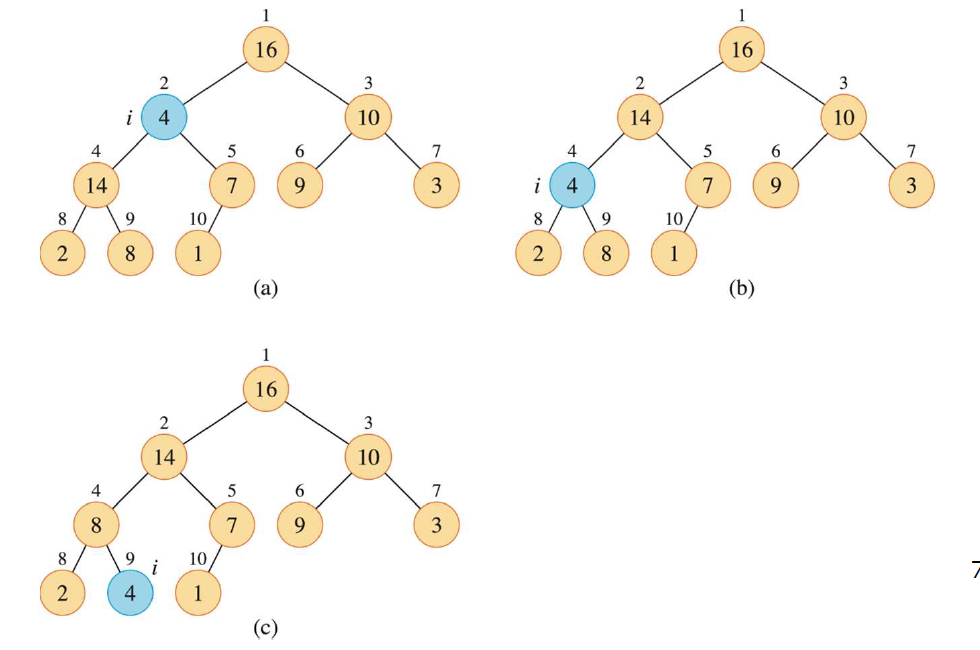
根结点和其左结点或者右结点发生元素交换，检查和交换的代价为 $\Theta(1)$ ，设子树规模为 $n$ ，左子树或者右子树最大规模为 $2n/3$ （这是结论，下面将证明） 。

这个递归式的表达式可以写为： $T(n) \leq T(2n/3) + \Theta(1)$ ，根据Master Theorem Case 2， $n^{\log_{2/3} 1} = n^0 = 1 \in \Theta(1)$ ，则递归式的时间复杂度 $T(n) = \Theta(\lg n)$ 。

下面证明左子树或者右子树最大规模为 $2n/3$ ：

我们知道，堆是一个完全二叉树的模型，它每一层将数据分成两个部分，它的高度可以通过： $(1/2)^i n = 1 \Rightarrow i = \lg n$ 。

堆的结点数n，我们可以计算得，最多结点数为全满的情况： $n_l = \sum_{(0,\lg n)} 2^i = 2^{\lg n} - 1$ ，最少的为最后一层仅有一个结点的情况： $n_r = \sum_{(0,\lg n-1)} 2^i + 1 = 2^{(\lg n-1)}$ 。

由于堆是对应一棵完全二叉树，根结点的左子树结点数 大于等于 根结点的右子树结点数。

对于一个完全二叉树，它的最后一层可能不是完全填满的。假设我们假设左子堆是一个高度为 $h$ 的满二叉树，右子堆是一个高度为 $h-1$ 的满二叉树。于是此时总高度为 $h+1 = \lg n$ 。

左子堆的结点数量： $n_l = \sum_{(0,h)} 2^i = 2^{(h+1)} - 1 = 2^h \times 2 - 1$ （因为有 $2^h + 2^{h-1} + 2^{h-2} + ... + 2 + 1$ 有h+1个数）

同理，右子堆的结点数量： $n_r = \sum_{(0,h-1)} 2^i = 2^h - 1$ ，总数为： $n = (2^{h+1} - 1) + (2^h - 1) + 1 = 2^{h+1} + 2^h - 1 = 2^h(2 + 1) - 1$ 。

左子树的最大规模： $(2^{(h+1)} - 1) / (2^h(2 + 1) - 1) = (2 \times 2^h - 1) / (3 \times 2^h - 1) < (2 \times 2^h) / (3 \times 2^h) = 2/3$

于是我们就得到了左子树规模为 $(2/3)n$ 。

当二叉树为满二叉树时，左右子树结点个数相等。经过上面的计算很容易知道，左右子树的规模均为 $(1/2)n$ 。所以堆维护的递归式为：

$T(n) \leq T(2n/3) + \Theta(1)$

$T(n) \geq T(n/2) + \Theta(1)$

根据Master Theorem Case 2，它们最后为 $T(n) = \Theta(\lg n)$ 。

建堆#

我们对一个数组，按照自底向上的顺序多次调用MAX-HEAPIFY，就能将这个数组转换为一个大根堆。于是有这样的代码：

1
BUILD-MAX-HEAP(A, n)
2
    A.heap-size = n
3
    for i = floor(n/2) down to 1
4
        MAX-HEAPIFY(A, i)

建堆过程的调整操作是从后往前遍历数组，对应完全二叉树调整顺序就是从倒数第二层往上调整，每层从右往左调整。

叶结点作为子树只有一个结点，一定符合堆性质，所以就从这些叶结点的父母结点开始调整，这就是一个自下而上的过程，只要所有子树都符合堆的性质，那么这个完全二叉树一定符合堆的性质，这样也就建堆完成了。

例如下面这个例子：

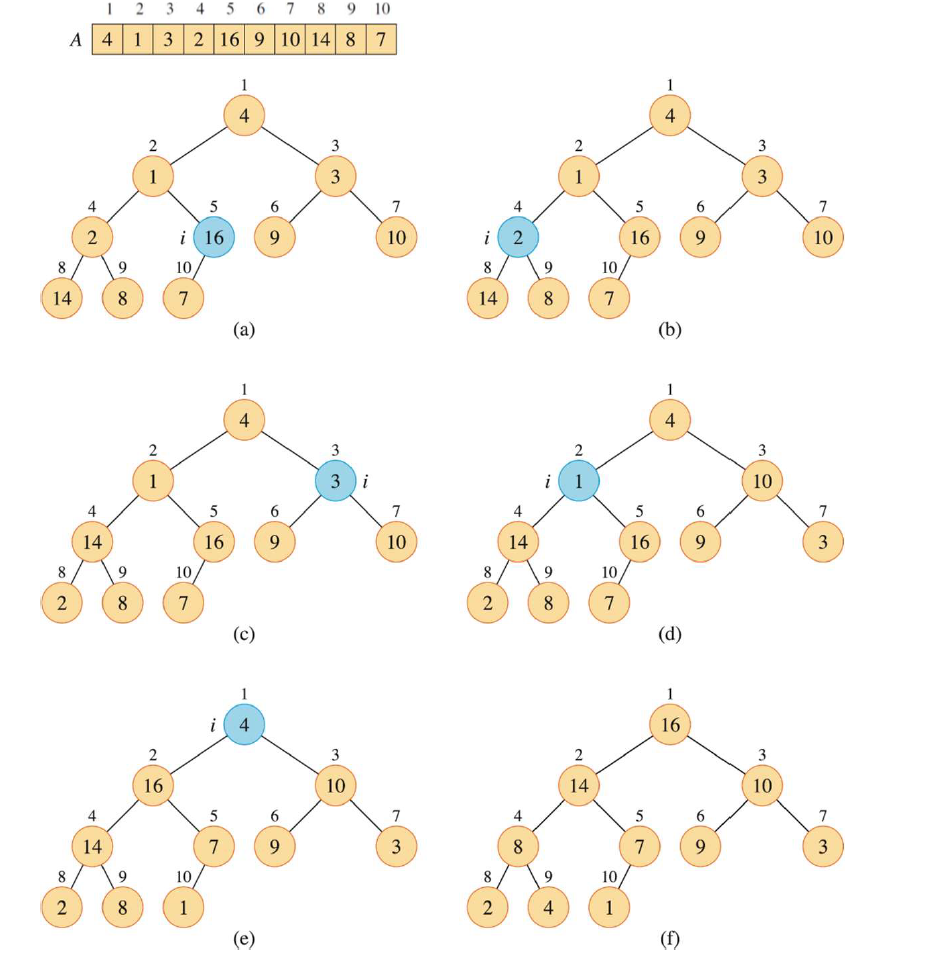
分析建堆算法，最简单的情况为for循环执行了n/2次，即 $MAX-HEAPIFY()$ 被调用了 $n/2 = O(n)$ 次，于是建堆的时间复杂度 $T(n) = O(n) \times O(\lg n) = O(n \lg n)$ 。

为了精确证明它，我们先需要找到，堆有多少个高度为h的结点。

在前面的证明中我们知道，一棵有n个节点的二叉树的深度为 $\lfloor \lg n \rfloor$ 。如果我们设在任何一个有n个元素的满二叉堆中，从叶子节点到某节点的高度为h（从叶子节点一直到某个节点的高度为h，而不是整个堆的高度为h）。那么该节点位于距离根节点 $\lfloor \lg n \rfloor - h$ 的深度（从根节点到该节点的路径上经过的边数）上。

举个例子解释：

1
     1
2
   /   \
3
  2     3
4
 / \   / \
5
4   5 6   7

这个堆是一棵完整的二叉树，并且有7个节点。我们可以看到，根节点的深度为0，第二层（包括节点2和节点3）的深度为1，第三层（包括节点4、5、6和7）的深度为2。

现在假设我们要找到节点5的深度。从上面的图中可以看出，节点5是叶子结点，距离叶子结点的高度为0，因此它的h=0。我们知道这个堆有7个结点，因此根据公式，节点5位于深度 $\lfloor \lg(7) \rfloor - 0 = 2$ 的位置。

所以在这一层，高度为h，一共有 $2^{\lfloor \lg n \rfloor - h} = 2^{\lfloor \lg n \rfloor}/2^h$ 个结点，因为 $2^{\lfloor \lg n \rfloor} \le 2^{\lg n} = n$ 。

我们有一个结论 $2^{\lfloor \lg n \rfloor} \le n/2$ ，可以通过数学归纳法证明它：

当n=1时:

$2^{\lfloor \lg(n) \rfloor} = 2^0 = 1 \le n/2 = 1/2$ ，不等式成立。

假设当n=k时，不等式成立，即 $2^{\lfloor \lg(k) \rfloor} \le k/2$ 。

当n=k+1时，有：

$2^{\lfloor \lg(k+1) \rfloor} = 2^{\lfloor \lg(k)+\lg(1+1/k) \rfloor} \le 2^{(\lg(k)+1)} = 2k \le (k+1)/2$ (由于k>=1)

因此，当 $n=k+1$时，不等式也成立。因此，对于所有的正整数n，都有 $2^{\lfloor \lg n \rfloor} \le n/2$

于是， $2^{\lfloor \lg n \rfloor}/2^h \le (n/2)/2^h = n/2^{h+1} \le \lceil n/2^{h+1} \rceil$ 。我们知道了在高度h处最多有 $\lceil n/2^{h+1} \rceil$ 个结点， $MAX-HEAPIFY$ 函数在高度h的时间需要O(h)。设每一层的消耗为c，那么我们就可以计算建堆的总消耗了。

用 $\sum_{(0,\lfloor \lg n \rfloor)} \lceil n/2^{h+1} \rceil \times c \times h$ 表示，对这个式子进行一些化简得：

于是建堆的过程，时间复杂度为 $O(n)$ 。

堆排序#

堆排序算法就是先建堆，并一个个删除头部结点，再维护堆即可。删除堆只需要将A[1]与A[A.size]交换，然后维护1的位置的结点即可。以大根堆为例：

1
HEAPSORT(A, n)
2
    BUILD-MAX-HEAP(A, n)
3
    for i = n downto 2
4
        swap(A[1], A[i])
5
        A.heap-size = A.heap-size - 1
6
        MAX-HEAPIFY(A, 1)

这个过程例如：

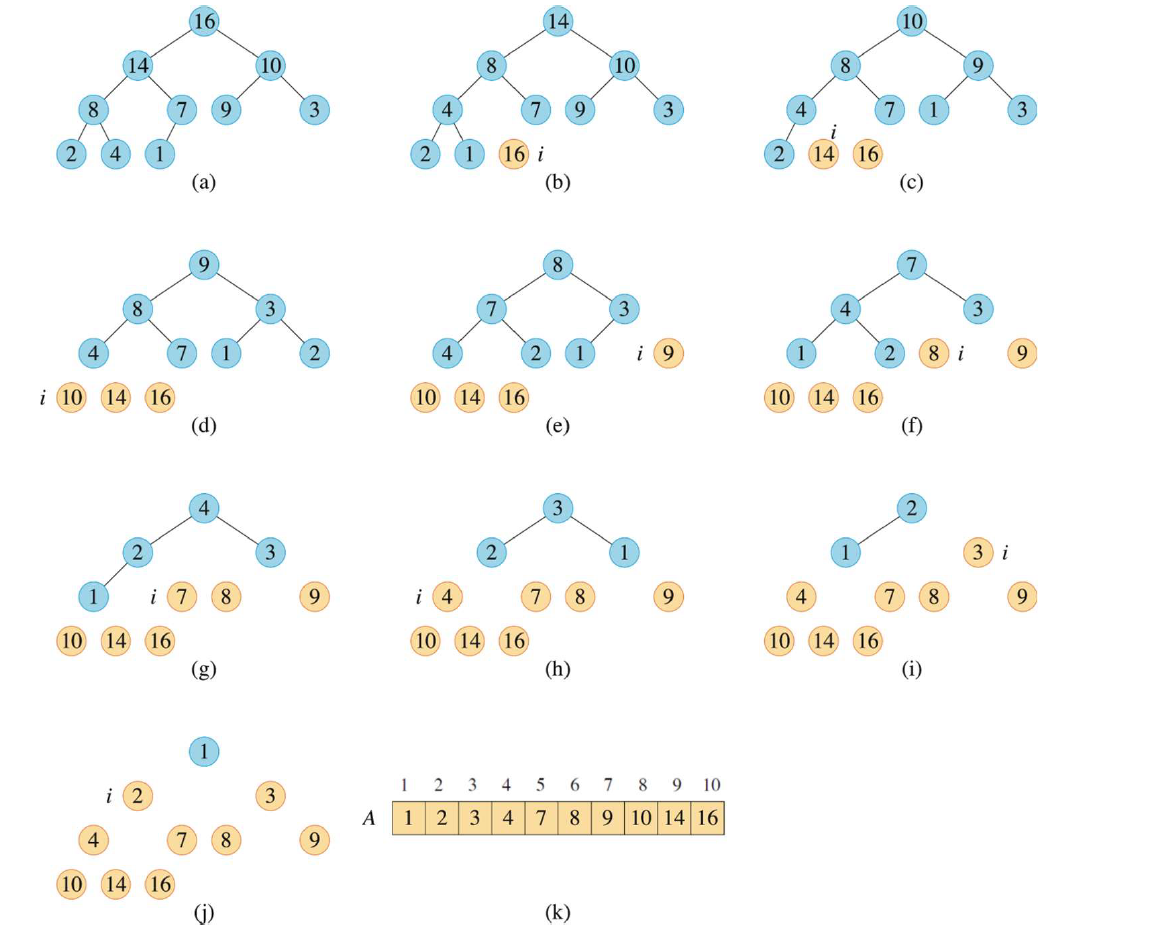
分析这个算法就非常简单了，一步步看：

• BUILD-MAX-HEAP: $O(n)$
• for loop: $n - 1$ times
• Exchange elements: $O(1)$
• MAX-HEAPIFY: $O(lgn)$

那么最后结果就是 $O(n \lg n)$

找到最大元素#

找到最大元素非常简单，就是堆的根。当然还需要检查是否堆已空。

1
MAX-HEAP-MAXIMUM(A)
2
    if A.heap-size < 1
3
        error "heap underflow"
4
    return A[1]

它的时间复杂度显而易见为Θ(1)。

取得并删除最大元素#

和堆排序一样，取得堆的根并维护堆：

1
MAX-HEAP-EXTRACT-MAX(A)
2
    max = MAX-HEAP-MAXIMUM(A)
3
    A[1] = A[A.heap-size]
4
    A.heap-size = A.heap-size - 1
5
    MAX-HEAPIFY(A, 1)
6
    return max

它的时间复杂度显而易见为O(lgn)。

替换并维护元素#

对于位置x，新的值为k，当k>=x时，x的值将会被替换为k，替换后并维护堆。

1
MAX-HEAP-INCREASE-KEY(A, x, k)
2
    if k < x.key
3
        error "new key is smaller than current key"
4
    x.key = k
5
    find the index i in array A where object x occurs
6
    while i > 1 and A[PARENT(i)].key < A[i].key
7
        exchange A[i] with A[PARENT(i)], updating the information that maps priority queue objects to array indices
8
        i = PARENT(i)

它的时间复杂度显而易见为O(lgn)。

插入元素#

为了使用之前替换的函数，我们需要先把插入位置置为极小值，再替换即可。

1
MAX-HEAP-INSERT(A, x, n)
2
    if A.heap-size == n
3
        error "heap overflow"
4
    A.heap-size = A.heap-size + 1
5
    k = x.key
6
    x.key = -∞
7
    A[A.heap-size] = x
8
    map x to index heap-size in the array
9
    MAX-HEAP-INCREASE-KEY(A, x, k)

它的时间复杂度显而易见为O(lgn)。

优先队列在队列不为空的情况下可以执行出队操作，移除队头元素，在队列未满的情况下可以执行入队操作，新增元素加入队尾，每次队列发生变化（增删改）均要重新调整堆，此外还要维护好句柄的映射。