
前言
本章为快速排序与对比分析插入排序、归并排序和快速排序。本章对应《Introduction to Algorithms 4th》的第七章Quicksort,为了应对期中考试,于是把这章提前到随机函数及随机算法(但会涉及一些随机算法内容)之前。具体目录请见学习笔记-算法设计与分析。
快速排序
快速排序描述
快速排序采用分治思想,一般分为三个步骤:
- 分解(Divide):子数组A[p…r]根据 pivot(主元)A[q] 进行分解,小于pivot的元素放到数组A[p
]中, 大于pivot的元素放在A[q+1 ] 中。 - 解决(Conquer):通过递归调用快速排序实现对 A[p
] 和 A[q+1 ] 的排序。 - 合并(Combine):因为子数组都是原值排序,此时 A[p
] 有序。
于是下面就是简单的快速排序的伪代码:
QUICKSORT(A, p, r) if p < r q = PARTITION(A, p, r) QUICKSORT(A, p, q - 1) QUICKSORT(A, q + 1, r)这个排序中我们只做了分解这件事,此时p是起始索引,r为结束索引,q是每个划分中的pivot。接下来再对子数组进行快速排序。
接下来,就是最关键的分组:
PARTITION(A, p, r) x = A[r] //我们默认选取最后一位为pivot i = p - 1 //i为此时lower side的最高位索引,初始化为数组0位 for j = p to r - 1 //p到r-1的元素进行分组 if A[j] ≤ x //若当前元素比pivot小 i = i + 1 //引索移动 exchange A[i] with A[j] //交换位置,即把元素放到A[p:i]里面去 exchange A[i + 1] with A[r] //循环结束,把pivot放到中间去 return i + 1 // new index of pivot我们一步步来看这个分组部分的代码,例如数组{2,8,7,1,3,5,6,4}的第一次分组:
-
确定初始化i,j,r位置,i代表的是lower side的最高位索引,此时还没有则为0;j此时是位置1,r在最后。我们用浅色表示还没处理的部分。
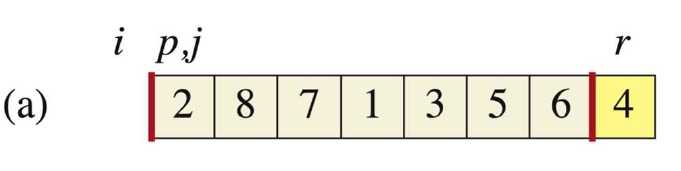
-
当j=1时,此时A[j]=2 < A[r],则移动i(i++到1的位置),并且让A[i]与A[j]交换,此时i=j=1,则不动。操作完后j++。我们用橙色表示比r小的部分。
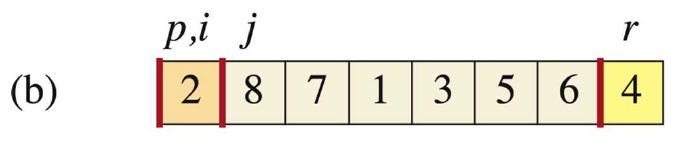
-
当j=2时,此时A[j]=8 > A[r],此时i不动,j++。我们用蓝色表示比r大的部分。
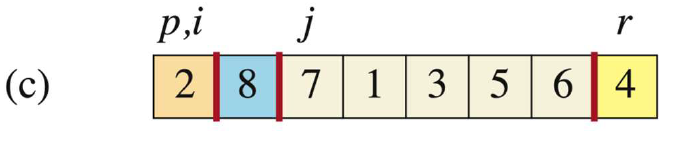
-
当j=3时,此时A[j]=7 > A[r],此时i不动,j++。
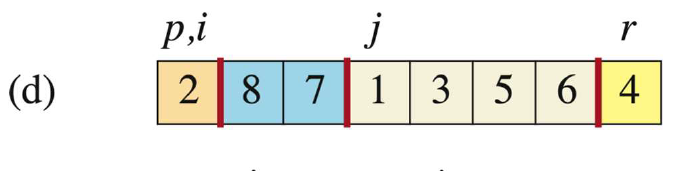
-
当j=4时,此时A[j]=1 < A[r],则移动i(i++到2的位置),并且让A[i]与A[j]交换,即A[2]与A[4]交换(2与8交换)。操作完后j++。

-
当j=5时,此时A[j]=3 < A[r],则移动i(i++到3的位置),并且让A[i]与A[j]交换,即A[3]与A[5]交换(3与7交换)。操作完后j++。
-
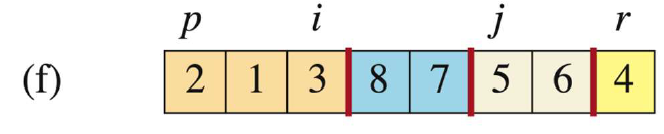
当j=6时,此时A[j]=5 > A[r],此时i不动,j++。
-
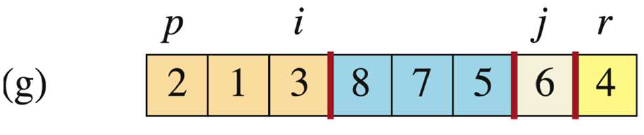
当j=7时,此时A[j]=6 > A[r],此时i不动,j++。
-
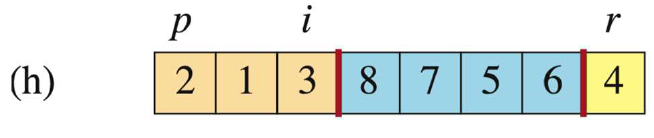
j=8 > p-1=7,跳出循环。把i+1位置(3+1 = 4,这是大于pivot的子数组的首元素地址)上的元素与pivot交换。(这样交换能保证pivot左边比pivot小,pivot右边比pivot大)
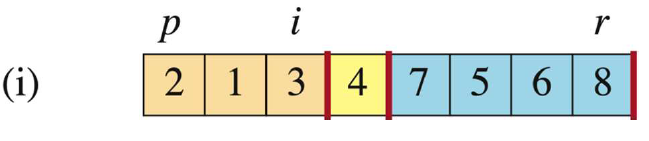
整个过程中只有一个循环,很容易知道它的时间复杂度为 。
快速排序的分析
最坏的情况
最坏的情况很容易算出,假设每次基本都是不平衡的划分,最后一层数组大小为空,则为T(0) = 0,则时间复杂度可以写为:
根据我们带入法,很容易得出它的最坏情况为 。下面是证明:
猜测 ,,则
最好的情况
在最平衡的划分,两个子问题都不大于n/2,均可看成对半划分,则
根据Master method,,应用第二条规则,得到此时最好的情况为 。
平均的情况
快速排序的平均情况的运行时间更接近于最好情况的运行时间,而不是最坏情况的运行时间之间。在之后随机函数的章节会进行证明。
在平均情况下,好的划分和坏的划分是随机分布的,假设好的划分是最好情况划分,坏的情况是最坏情况划分,当好坏划分交替出现时,一个坏的划分和一个好的划分等价于一个好的划分,所以,快速排序的平均情况的运行时间很可能是 ,只是隐藏的常数因子比最好情况的隐藏的常数因子略大。这个将在之后的章节证明。
排序分析
本章在这里还分析其他两种排序——插入排序与归并排序,以及它们的改进版本。
插入排序
插入排序是在第一篇(原书第二章)就举的例子,用于最原始的算法分析的入门。它的伪代码为:
INSERTION-SORT(A, n) for i = 2 to n key = A[i] j = i - 1 while j > 0 and A[j] > key A[j + 1] = A[j] j = j - 1 A[j + 1] = key很明显,插入排序是在固定了一段有序数组后,将未排序数据插入有序数组中形成一个新的有序数组。这个过程有两重循环,在最坏的情况下,,其中a,b,c为常数,即
最好情况则是当待排序序列为正序状态,则遍历完整个序列,当插入元素时,只比较一次就够了,所以此时复杂度为 。
归并排序
归并排序使用了分治法的思想,对它的分析我们可以使用前一篇(原书第三章分治法)中的三种方法去解决。下面是归并排序递归部分的伪代码:
MERGE-SORT(A, p, r) if p ≥ r return q = ⌊((p + r) / 2)⌋ MERGE-SORT(A, p, q) MERGE-SORT(A, q + 1, r) MERGE(A, p, q, r)它的操作原理是:假如初始序列含有 n 个记录,则可以看成是 n 个有序的子序列,每个子序列的长度为 1。然后两两归并,得到 n/2 个长度为2或1的有序子序列;再两两归并,……,如此重复,直到得到一个长度为 n 的有序序列为止。
它采用了分治法的思想,通过自上而下的递归和自下而上的迭代来实现。
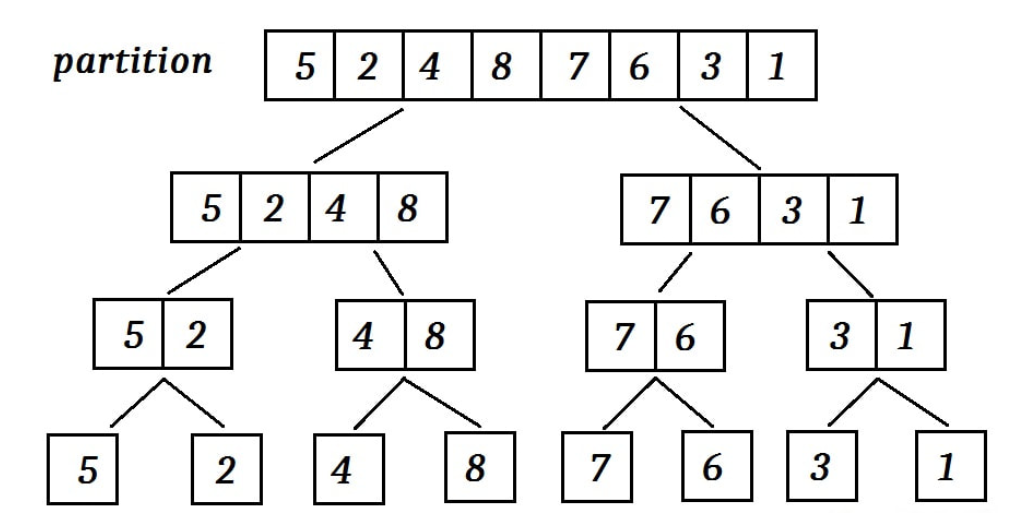
分析这个算法,若规模足够小,即n=1时,本身就是有序的,此时 ;
一般情况下,观察递归式,每次递归大致都是对半分,然后对两个一般再分,此时可以看做分为了两个规模为n/2的子问题()。递归最后还需要计算合并的时间,我们来看合并部分的代码:
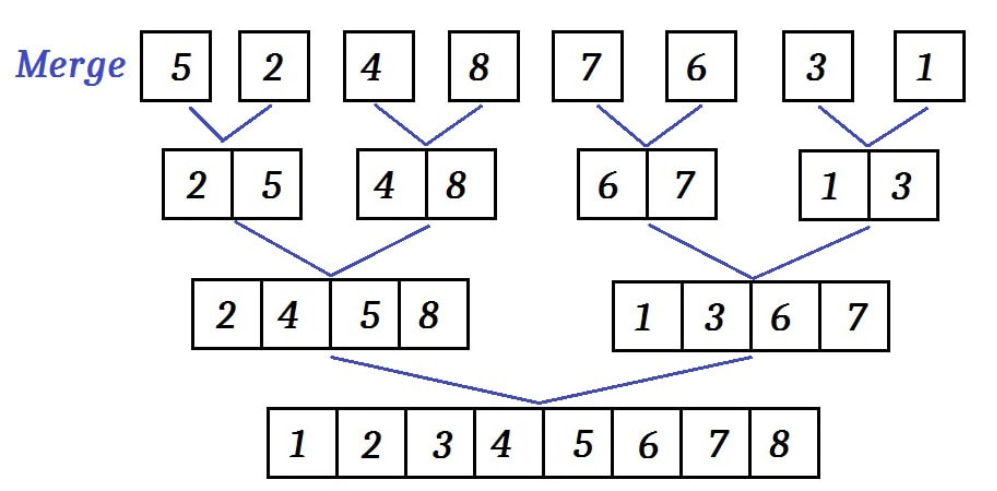
MERGE(A, p, q, r) nL = q - p + 1 //左半部分长度 nR = r - q //右半部分长度 let L[0 : nL - 1] and R[0 : nR - 1] be new arrays for i = 0 to nL - 1 //单独把左半部分放入一个数组 L[i] = A[p + i] for j = 0 to nR - 1 //单独把右半部分放入一个数组 R[j] = A[q + j + 1] i = 0 j = 0 k = p //记录原来A数组的索引 while i < nL and j < nR //逐位比较 if L[i] ≤ R[j] //如果左半部分这一位小于右半部分这一位 A[k] = L[i] //则把左半部分这一位放回原数组中 i = i + 1 else A[k] = R[j] //否则放右半部分那一位 j = j + 1 k = k + 1 while i < nL //如果j先到了nR,即左半部分有剩余,右半部分放完了 A[k] = L[i] //把左半部分剩余的接过去 i = i + 1 k = k + 1 while j < nR //如果i先到了nL,即右半部分有剩余,左半部分放完了 A[k] = R[j] //把右半部分剩余的接过去 j = j + 1 k = k + 1观察其合并的过程,可以知道,合并是一个逐位比较的过程,其中通过索引判断是否放完。很明显,这是个 的算法。
故对于归并排序:
分析这个算法,我们可以直接使用Master method,,则它的时间复杂度为
或者使用递归树法:
令:
画一个递归树
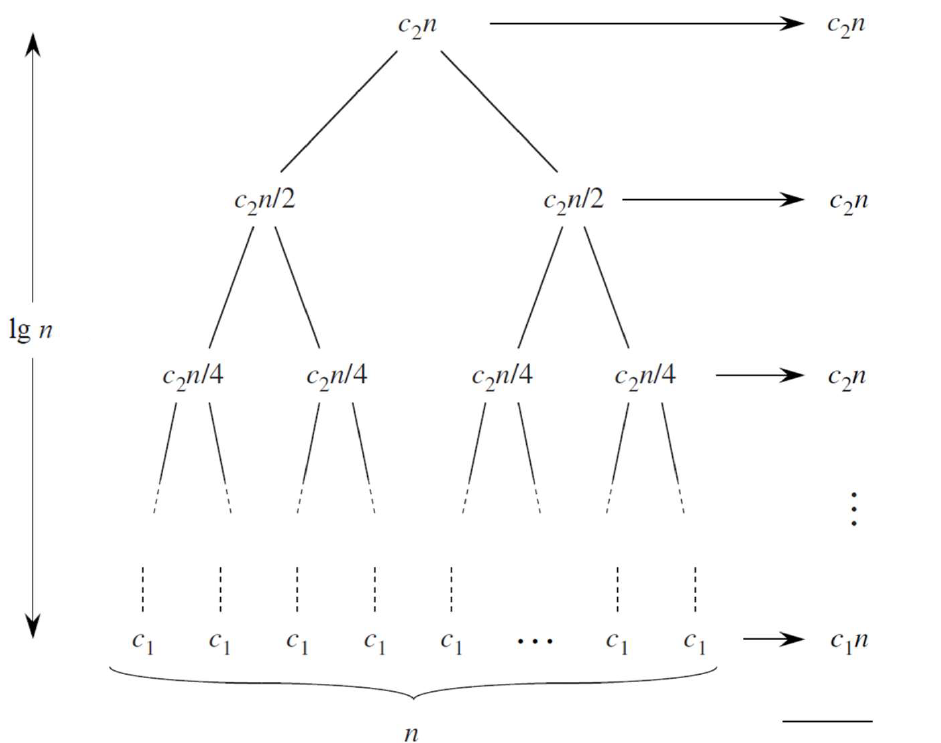
根据递归树法,设在第i层时,规模达到1,则 。此时因为左右子问题规模一样,则整个递归树的高度为 。
在高度为i的层数,我们根据层与层元素的个数的关系可以知道,第i层有 个元素,在 层(最后一层),有 个元素。
对于每一层,我们相加都是 ,而在最后一层则为 ,于是我们整体的时间就可以计算了:
故最后,归并排序的时间复杂度为 。
递归插入排序
我们可以把插入排序表示为如下的一个递归过程。
为了排序A[1.n],我们递归地排序A[1,n-1],然后把A[n]插入已排序的数组A[1,n-1]。
每一次递归中,我们都需要插入元素到有序数组中,这个过程需要一个循环。我们用递归代替外层循环,递归每次规模为n-1,于是我们就可以得到下面的伪代码:
INSERTION-SORT(A, n) if n < 2 return INSERTION-SORT(A, n-1) temp = A[n] i = n - 1; while i > 0 if A[i] < temp break A[i + 1] = A[i] i = i - 1 A[i + 1] = temp我们可以用这样的递归式表示它的运行时间:
我们分析它非常简单,对它画递归树,是一条直线:
除了最后一层外是一个等差数列,有n-1项,求和得
二分法插入排序
在子数组已经排序的情况下,我们可以用二分查找(binary search)找到要插入的区间,使得插入排序的效率提升。
如果序列A已排好序,就可以将该序列的中点与v进行比较。根据比较的结果,原序列中有一半就可以不用再做进一步的考虑了。二分查找算法重复这个过程,每次都将序列剩余部分的规模减半。
用循环二分找到区间的伪代码为:
BINARY-SEARCH(A, n, x) left = 0 right = n - 1 while left ≤ right mid = ⌊(left + right) / 2⌋ if A[mid] == x return mid else if A[mid] < x left = mid + 1 else right = mid - 1 return NIL或者使用递归:
BINARY-SEARCH(A, left, right, x) if left > right return NIL mid = ⌊(left + right) / 2⌋ if A[mid] == x return mid else if A[mid] > x return BINARY-SEARCH(A, left, mid - 1, x) else return BINARY-SEARCH(A, mid + 1, right, x)我们可以通过这个算法找到插入的区间范围,我们用递归的版本很容易看出二分查找的时间复杂度:每一次都尽可能的分成一个n/2规模的子问题。,根据Master method,, 则此时 。
我们仅仅只是优化了查找时间,我们插入的步骤还涉及到其他元素的向后移动,这个过程也是O(n)的,导致无法将时间复杂度降低至 ,插入排序在二分查找下仍然是 的算法。
归并排序中对小数组采用插入排序
虽然插入排序的最坏情况运行时间 比归并排序的最坏情况 运行时间差,但插入排序在数据量很小时在许多机器上运行的更快()
所以我们可以用插入排序修改归并排序的递归树。使其不要到只有一个元素再进行合并,而是到一个设定的数组长度时,最小的子数组(归并段)执行插入排序,设最小子数组(归并段)长度为 k ,分成 n/k 个子数组(归并段)。
插入排序对它最快 解决,最慢的情况 解决。
对于归并排序:
它的递归树:

根据设定,我们把原数组分成 n/k 个子数组,此时递归树的高度h计算:
递归树每一层合并时间为,则到n/k的合并一共耗费时间:
则此时把它们时间合并起来,可以得到归并排序下使用插入排序的时间:,要使它与标准的归并排序具有一样的运行时间,需要令
猜测 ,
那么k的最大值就是 ,c是一个正常数。
快速排序的优化——随机算法
与始终采用 作为主元的方法不同,随机抽样是从子数组 中随机选择一个元素作为主元。 我们称其为随机抽样(random sampling)。
为达到这一目的,首先将 (最后一位)与从 中随机选出的一个元素交换。通过对序列 的随机抽样,我们可以保证主元元素 是等概率地从子数组的r-p+1个元素中选取的。
我们修改一下我们的快速排序即可:
RANDOMIZED-PARTITION(A, p, r) i = RANDOM(p, r) exchange A[r] with A[i] return PARTITION(A, p, r)
RANDOMIZED-QUICKSORT(A, p, r) if p < r q = RANDOMIZED-PARTITION(A, p, r) RANDOMIZED-PARTITIONQUICKSORT(A, p, q - 1) RANDOMIZED-PARTITIONQUICKSORT(A, q + 1, r)RANDOMIZED-PARTITION将任意常数比例的元素划分到一个子数组中。 则算法的递归树的深度为,并且每一层上的工作量都是O(n)。即使在最不平衡的划分情况下,会增加一些新的层次,但总的运行时间仍然保持是 。
最坏情况下,RANDOMIZED-PARTITION被调用 ,解得。
最好情况下,RANDOMIZED-PARTITION被调用 ,解得 。
最好情况和最坏情况RANDOMIZED-PARTITION被调用次数都是,这并非巧合,因为数组中每个元素都可能被选为pivot。
快速排序的优化——三路快速排序
当序列中所有元素都相等,此时我们的总是存在q=r,我们可以发现它的时间复杂度为 (因为小于等于pivot的在一边,其他的另外一边,相等时非常不平衡)。当数组中重复元素非常多的时候,等于pivot的元素太多,那么数组就会分成极度不平衡的两个部分,因为等于pivot的一部分总是集中在数组的一边。
此时我们就提出了三路快速排序来解决这个问题。它的思想是:分成小于pivot、大于pivot和等于pivot的三部分,如图:
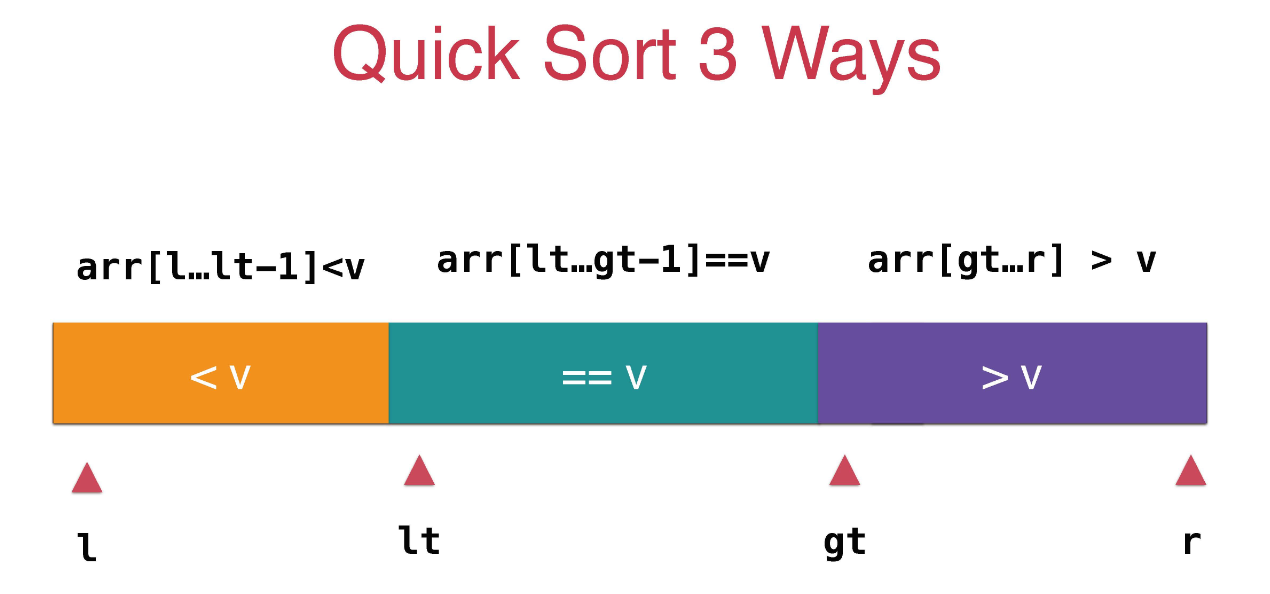
我们进行下面的修改:
PARTITION'(A, p, r) x = A[p] low = p high = p for j = p + 1 to r if A[j] < x y = A[j] A[j] = A[high + 1] A[high + 1] = A[low] A[low] = y low = low + 1 high = high + 1 else if A[j] == x exchange A[high + 1] with A[j] high = high + 1 return (low, high)此时最后RANDOMIZED-PARTITION也能达到 。
后记
本章为快速排序、对比分析插入排序、归并排序和快速排序以及一些优化。

