
前言
想象一个复杂的城市供水问题,它由 水库 向 城市 供水。通常来说,传输的管道不可能是一条笔直的管道,因为这样修建和维护的成本都很高。它会像电网传输一样,中间有许多管道连接不同的节点,以方便从多处获取和维护。
在设计的时候,每条管道都有一个 容量上限,超过这个量,管道就要爆了。但因为地区和政策的不同,可能每条管道设计容量并不相同,就像铁路网络中不是每条路线都能跑 350 km/h 一样。
对于城市而言,它在设计输水管道路线的时候需要考虑的是:在不超过任何管道容量的前提下,最多能从水库送多少水到城市?
在计算机中,这样的问题通常使用基于图论的 流网络 (Flow Network) 来描述。那么问题将转换为 最大流 (Maximum Flow) 问题:在一个流网络中,最多能传输多少的流?
本章将介绍图论中经典的最大流问题,这一章不仅是学习一个算法,更是学习一种名为 “对偶性” (Duality) 的深刻思维方式。
流网络
在前言中,我们已经通过一个现实问题了解了流网络的概念,现在让我们把这个直观概念转化为严格的数学语言。
Defination - Flow Network流网络 是一个有向图,其中:
- 每条边 有一个非负的容量
- 如果 ,那么不存在一条反方向的边,即
- 如果 ,则约定
- 存在两个特殊顶点:
- 源点 (source) :流的起点
- 汇点 (sink) :流的终点
- 对于每个顶点 ,存在一条路径
这个定义我们可以将其转换为刚才提到的现实例子:
- 顶点 (vertex) → 管道交汇处(泵站、分流点)
- 边 (edge) → 管道
- 容量 (capacity) → 管道的最大承载量
- 源点 (source) → 水库(只出不进)
- 汇点 (sink) → 城市(只进不出)
如下图,这是一个简单的流网络。
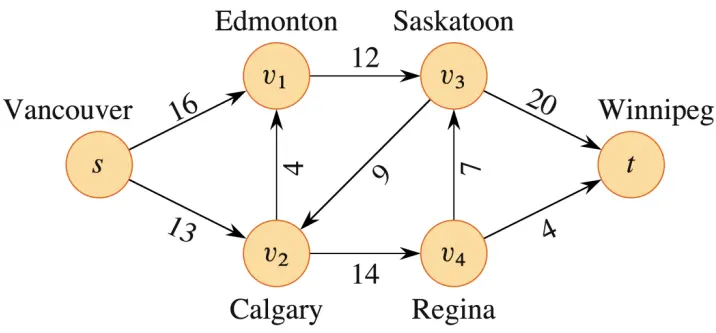
对于管道中的水,即 流 (Flow),我们也可以给出数学上的定义:
Defination - Flow流网络 中的流是一个函数 ,满足:
性质 1:容量限制 (Capacity Constraint)
每个管道中流的实际量不能超过当前管道的最大承载量。
性质 2:流量守恒 (Flow Conservation)
除了源点和汇点,其他每个点流入 = 流出。流进入一个结点的速率比较与其离开结点的速率相等。
流 的值 定义为从源点 净流出 的流量:
它就是从源点流出的总流量减去流入源结点的总流量,在通常情况下,源点不会有流的流入,因此大多数情况下:
值得注意的是:
- 对于性质2的流量守恒,实际是指流入一个非源点或汇点的结点的流的 总流量 必须等于流出该结点的 总流量 ,而不是每条边流入的量流出时都相等,如下方的表示。
流入 流出│ │▼ ▼┌─────────┐ ┌─────────┐5 ——→ │ │ │ │——→ 3│ v │ === │ v │7 ——→ │ │ │ │——→ 9└─────────┘ └─────────┘流入: 5 + 7 = 12 流出: 3 + 9 = 12
- 流的量 中的符号 表示的是流的值,而非绝对值,因为不存在负数的情况。
|f| = 5 + 8 = 13↓┌────────────────────────┐│ 5 ││ s ——————→ v₁ ││ │ ││ │ 8 ││ ▼ ││ v₂ ——————→ ... ——→ t │└────────────────────────┘
现在我们可以正式定义这章的核心问题了:
Defination - Maximum Flow最大流 (Maximum Flow) 问题:给定流网络 ,源点 ,汇点 ,容量函数 ,
求:一个流 ,使得 最大
如果我们将流标注在流网络上,可以得到如下的图。其中每一条边 标注的是 ,即当前管道的流 / 管道的总承载量,读作 out of 。
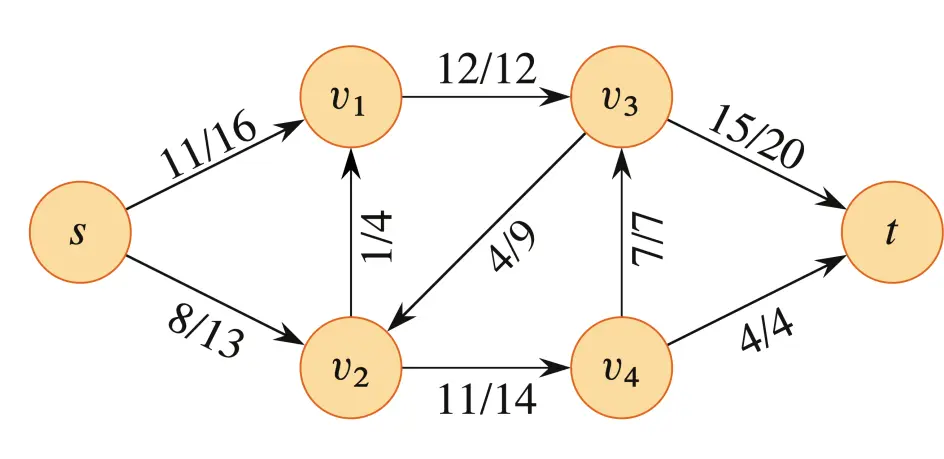
在这个例子中,。
在传统的流网络中,若存在边 ,则图中不允许出现反方向的边,即 。但现实世界中经常会遇到中间商之间互相交易的情况,会出现如下 (a) 的情况。我们称边 和边 是 反平行 (antiparallel) 的。图 (b) 提供了一个简单的转换网络,使得网络符合传统流网络的限制条件。它通过加入一个新结点 将其中一条边分解为两段,并且设计两条新设立的边(输入 和 输出的边)与原来分解的边的容量相同。
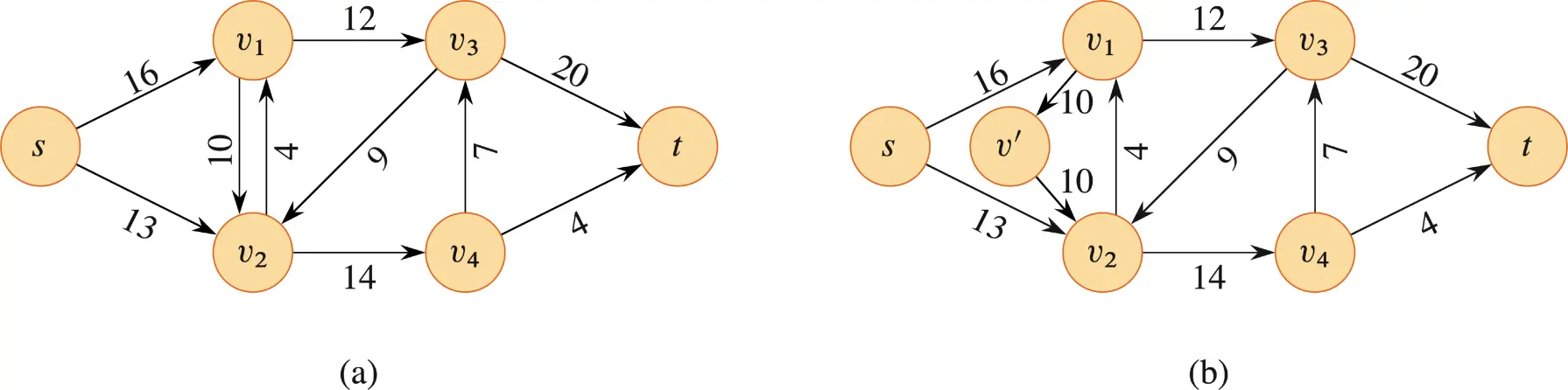
在之后本章的讨论中,我们将会经常见到这样的反平行表示。
Ford-Fulkerson 方法
残存网络
我们可以想象一个输水管道 ,它的容量是 升/秒。目前,你决定往里灌了 3 升/秒的流 ()。现在问:还能不能再多送一点?
如果路径上每条边都还有 剩余容量 (Forward Edge),那我们就能沿着这条边再推送一些流量
显然,此时管道的剩余容量为 升/秒。我们可以用 的边,权重为 7 来表示。
但是我们在分配流的时候,发现刚才那 3 升水送错了,导致别的地方堵死了。此时可以通过这条反向边,把这 3 升水“推回去”,退还给 ,让 把水送去别的更有用的路径。此时反向边的 ,权重为 3。
这种能够”撤销”之前的错误决定的机制形成的流网络就是 残存网络 (Residual Network) 。
在残存网络中,边 的值不在是 ,而是使用该方向上的 残存容量 (Residual Capacity),用来表示还能额外传递的流的容量。我们用数学语言来定义它可以得到:
Defination - Residual Capacity给定流网络 和流 ,边 的残存容量定义为:
此外,我们还需要添加反向边,用于表示 “撤销” 的能力。
如果 ,那么反向边 的残存容量是:
┌─────────────────────────────────────────────────────────────────┐│ ││ 原图中的一条边: 残存网络中变成: ││ ││ c = 10 c_f = 10 - 3 = 7 ││ u ──────────▶ v u ──────────────────▶ v ││ f = 7 ││ c_f = 3 (反向边) ││ u ◀────────────────── v ││ ││ 含义: ││ • 正向还能再流 3 ││ • 反向可以"撤销" 7 ││ │└─────────────────────────────────────────────────────────────────┘这样重新构造的网络,即 残存网络 (Residual Network) 可以定义为:
Defination - Residual Network给定流网络 和流 ,残存网络 定义为:
残存网络包含所有” 还有容量 “的边(无论是正向剩余还是反向撤销)。
增广
如下图 (a) 是一个流网络 及其流 。(b) 则是该图的残存网络 。其中以阴影部分为例子,残存容量 ,,。对于残存容量为 0 的边则不会画出。
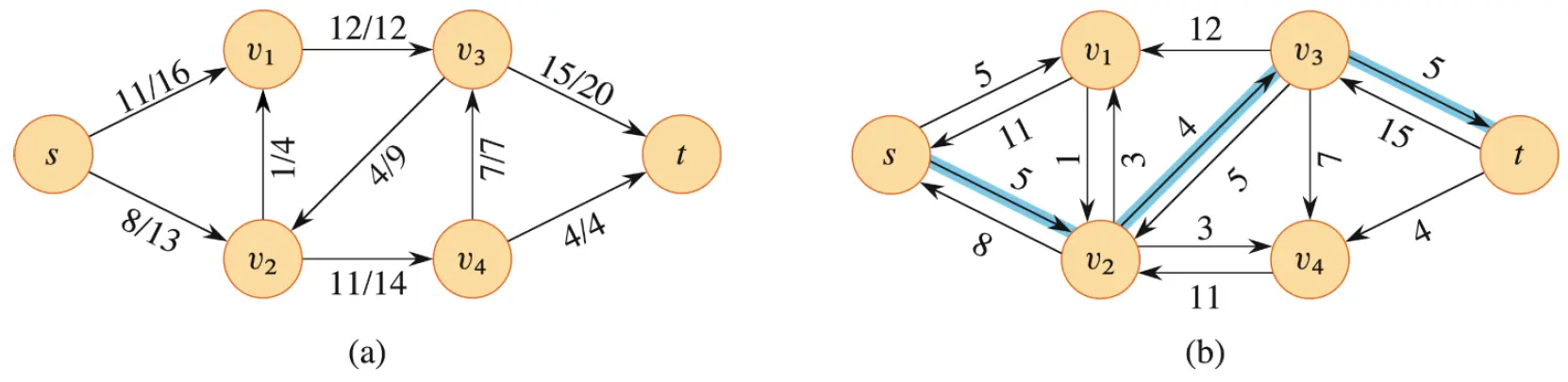
对于一条这样的 的路径,如图 (b) 阴影部分:,我们可以最多推送 的流。
那么对于残存网络 ,在 中寻找一条从 到 的简单路径,这个路径就是 增广路径 (Augmenting Path)。刚才例子中, 就是一条增广路径 。
我们称在一条增广路径 上能够为每条边增加流量的最大值为路径 的残存容量,表示为:
它会被路径 上能推送的流的最小值决定。
我们较为规范地定义增广公式:
Defination - Augmentation若我们有原始流网络 中的一个流 ,残存网络 中的一个流 ,定义 (读作 “f augmented by f prime”)为流 对流 的 增广 (Augmentation) 函数:
这个公式看着都吓人,我们可以逐步解析它:
回忆一下,残存网络 中的边有两种来源:
- 类型 1:正向边 表示 还能再增加多少流,残存容量 当 时存在。
- 类型 2:反向边 表示 可以撤销多少流,残存容量 ,当 时存在。
假设在残存网络 中, 是一个从 到 的流。对于原图中的边 :
- = 在残存网络中,沿正向边 流过的量 → 意味着:我们想 增加 原图中 的流量。
- = 在残存网络中,沿反向边 流过的量 → 意味着:我们想 撤销 原图中 的流量。
所以增广公式的含义是:
原来的流量 增加的量 撤销的量 │ │ │ ▼ ▼ ▼新流量 (u,v) = f(u,v) + f'(u,v) - f'(v,u)下面是一个例子:
原图 G 中:
u ─────────────────▶ v 容量 c(u,v) = 10 当前流 f(u,v) = 7残存网络 中:
u ─────────────────▶ v 正向边,残存容量 = 10 - 7 = 3
u ◀───────────────── v 反向边,残存容量 = 7- 如果我们打算 增加 2 容量的水,,。那么新流量 = 。此时 原来流 7,现在多流 2,变成 9。
- 如果我们打算 撤销 3 容量的水,,。那么新流量 = 。此时 原来流 7,撤销 3,变成 4。
- 如果我们打算 增加 1 容量的水,同时 撤销 2 容量的水,那么等价于 撤销 1 容量的水,,。那么新流量 = 。此时 增加 1,撤销 2,净效果是减少 1。
那么根据我们的定义,可以得到一个重要的引理:
Defination - Augmentation Lemma 1是图 的一个增广流,其值为
- |f| 的值表示图 原本的流的值。
- |f’| 的值表示残存网络 的流的值。
当我们找到一条增广路径 时,实际上是在残存网络中构造了一个特殊的流 ,我们定义为 。我们有这样的另一条引理:
Defination - Augmentation Lemma 2设图 是图 的残存网络, 为残存网络 中的一条增广路径,则定义 是残存网络的一个流:
其中 是路径 的瓶颈容量。
此时要求其值:
我们可以把引理2代入到引理1中得到:
流 增加 的量,将会获得一个新的流 ,这个流的值更接近于 最大流。
回到我们之前的一个例子中,图 (a) 是一个流网络 ,此时 ,图 (b) 则是它的残存网络 。我们增加了图 (c) 和图 (d)。
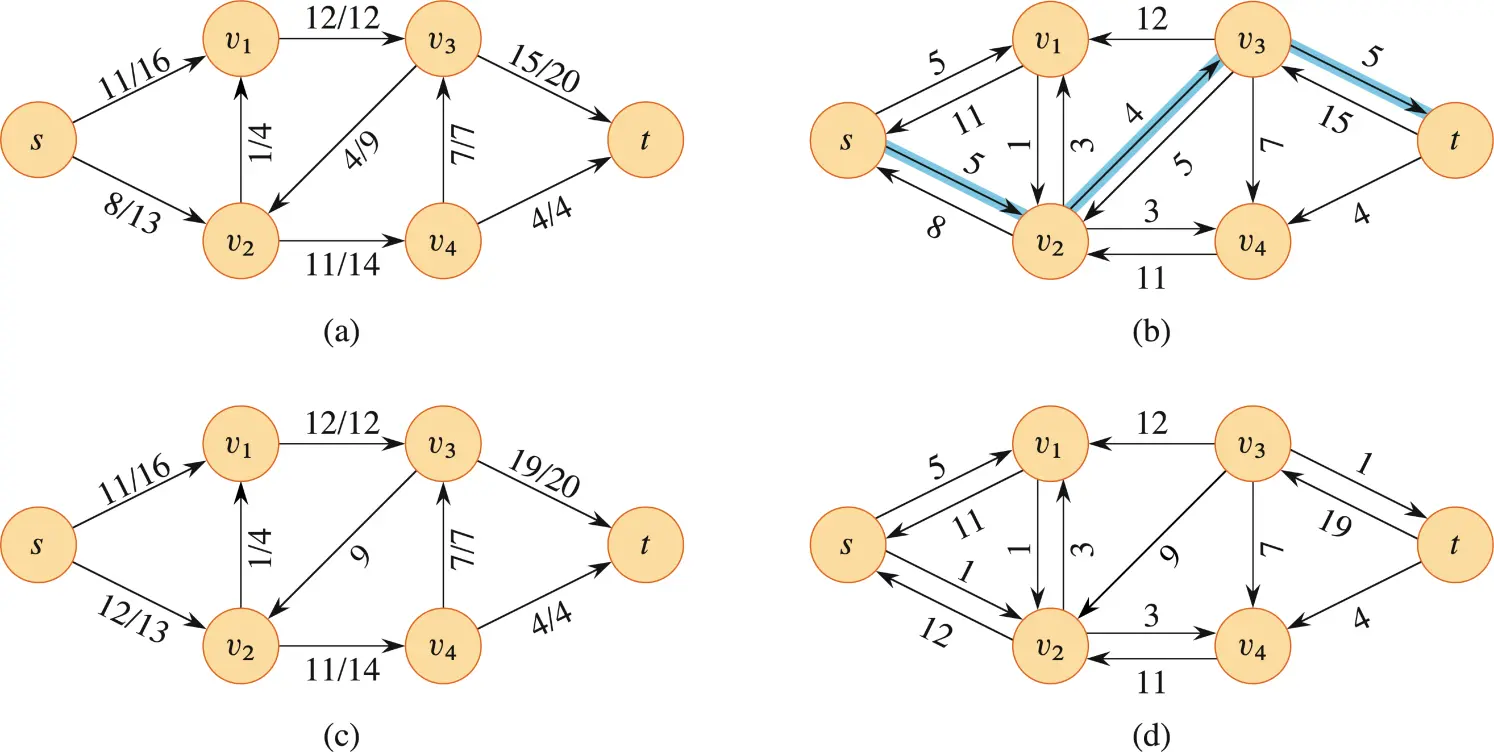
图 (c) 中 使用了沿着增广路径 (图 (b) 阴影部分) 增加而导出的流。我们在之前计算过它的残存容量 ,所以此时图 (c) 的流就是一个增广流,其值为:, 是因为增加了残存容量 ,而 不变因为没有采用包含它的增广路径。对于没有残存容量的边,例如 ,图中则不会显示。
我们将此时的图 (c) 重新转换为残存网络可以得到图 (d)。
基本 Ford-Fulkerson 算法
现在我们可以描述完整的 Ford-Fulkerson 方法了,他的逻辑非常简单:
- 初始化流量为 0。
- 循环 (在残留网络 中存在一条从 到 的增广路径 ):
- 找出路径 上的瓶颈容量(即路径上最小的剩余容量)。
- 沿着这条路径增加流量(更新正向流,同时也更新残留网络中的反向边)。
- 当找不到增广路径时,算法结束,当前流即为最大流。
基本 Ford-Fulkerson 算法使用了 DFS 去查找增广路径,其时间复杂度为 ,其中 是边的数量, 是最大流的值。
FORD-FULKERSON(G, s, t): 初始化所有边的流量 f(u,v) = 0
while 残存网络 Gf 中存在 s→t 的路径 P: // 找瓶颈 Δ = min{ cf(u,v) : (u,v) ∈ P }
// 增广 for each edge (u,v) in P: if (u,v) 是原图中的边: f(u,v) = f(u,v) + Δ else: // (u,v) 是反向边,对应原图的 (v,u) f(v,u) = f(v,u) - Δ
更新残存网络 Gf
return f我们通过一个例子来模拟一次这个过程:假设有如下的流网络图
s / \ 10 10 / \ ▼ ▼ a ─────► b | 1 | \ / 10 10 \ / ▼ t| 边 | 容量 |
|---|---|
| s → a | 10 |
| s → b | 10 |
| a → b | 1 |
| a → t | 10 |
| b → t | 10 |
-
初始状态,所有边的流量初始化为 0:当前流 。它的残存网络和原图一样。
-
第一次增广,假设选择了增广路径为:。瓶颈值 。我们更新网络:
此时流量是 。
图 :
s/ \1/10 0/10/ \▼ ▼a ─────► b| 1/1 |\ /0/10 1/10\ /▼t残存图 :
——> s| / \1 | 9 10|/ \▼ ▼a ◄──── b| 1 |\ /↑10 9 |\ / | 1▼ |t ———| -
第二次增广,假设选择了增广路径为:。瓶颈值 。我们更新网络:
此时流量是 。
图 :
s/ \1/10 9/10/ \▼ ▼a ─────► b| 1/1 |\ /0/10 10/10\ /▼t残存图 :
——> s <——| / \ |1 | 9 1 | 9|/ \|▼ ▼a ◄──── b| 1 ↑\ |10 | 10\ |▼ |t ———| -
第三次增广,假设选择了增广路径为:。瓶颈值 。我们更新网络:
此时流量是 。
图 :
s/ \10/10 9/10/ \▼ ▼a ─────► b| 1/1 |\ /9/10 10/10\ /▼t残存图 :
——> s <——| \ |10 | 1 | 9| \|| ▼a ◄──── b| 1 ↑↑\ |9 | 1 | 10| \ || ▼ ||—— t ———| -
第四次增广,假设选择了增广路径为: (注意:增广路径是残存图中的,而不是原图中的)。瓶颈值 。我们更新网络:
- : 注意,这里走了一个反向边,所以是减 1,意味着”撤回”之前 的流量。
当前流量
图 :
s/ \10/10 10/10/ \▼ ▼a ─────► b| 0/1 |\ /10/10 10/10\ /▼t残存图 :
——> s <———| |10 | | 10| || |a ────► b↑ 1 ↑| |10 | | 10| || ||—— t ———|
通过这个过程可以看出,反向边 = “后悔药” = “重新分配的机会”。当你走反向边 时,实际含义是:我决定少用一点 这条边,把配额让给更好的路径。
割与最大流最小割定理
我们已经了解了 Ford-Fulkerson 方法的过程了,但是它有一个很明显的缺陷:最后找的最大流是真的最大流吗?我们目前还不知道,接下来就需要引入割的概念。
从一个幽默的例子开始吧:假设你是敌方间谍 🕵️,想要切断城市的供水,你需要 最少 切断多大容量的管道,使得水厂的水完全无法到达城市?
我们称这样的问题是 最小割 (Min-cut) 问题。
在图论里,割 (Cut) 就是一种把图一分为二的分类法。我们同样通过数学语言进行定义:
Defination - Cut流网络 的一个割 是对顶点集 的一个划分,满足:
- (源点在 中)
- (汇点在 中)
- 且
你可以想象,拿出一把红色的剪刀,在纸上的流网络图中间随意画一条线,把 和 彻底隔开。这条线切断的所有管道,就是这个“割”所涉及的边。
如下图是一个割的例子,它将图分成了:
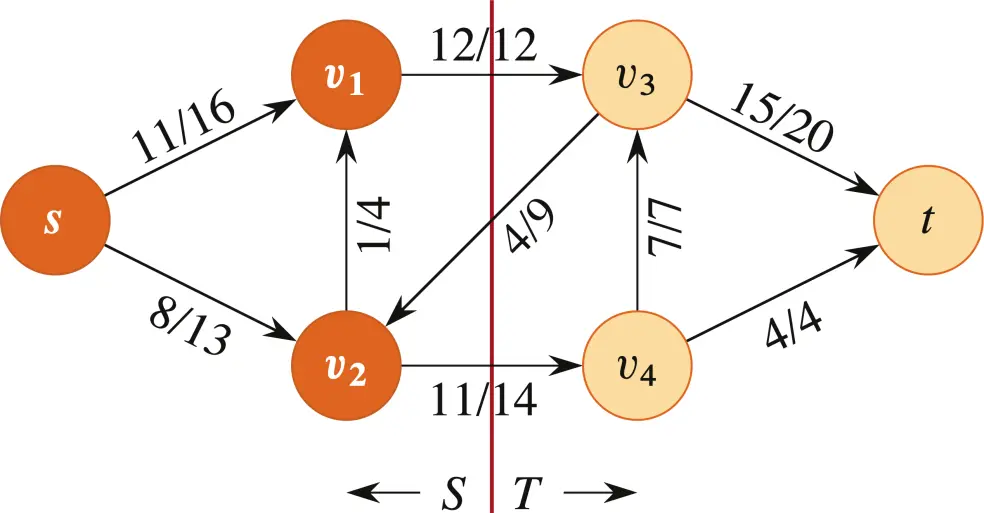
对于同一个割 ,有两个不同的度量标准:
Defination - Cut Capacity and Flow
割 的容量定义为所有 从 到 的边 的容量之和:
这是瓶颈的理论上限。注意:它 只计算从 指向 的边的容量之和。
给定流 ,跨越割 的净流量定义为:
它表示当前流的状态,数值上 (等于从 流向 的实际流量) 减去 (从 流回 的实际流量)。
我们之前提到的图片中,割的容量
对于当前割,它的净流量
我们发现了一个巧合: 是图 的一个流,,对于当前割,它的净流量 。这其实是对任意割都成立的,我们有这样的引理:
Defination - Cut Lemma 1对于任意流 和任意割 :
这现象第一眼感觉很反直觉,但是仔细想想确实如此。想象一条宽阔的河流(流网络)。
- 你在源头测流速,是 100。
- 你在中游随便找个截面切一刀(割),测流过截面的净水量,肯定也是 100。
- 你在入海口测,还是 100。
无论你怎么切这一刀(哪怕切得很歪,绕来绕去),只要把 和 分开了,流过这条线的净流量永远守恒,等于总流量。
此外,我们再考虑一下流的限制问题,很容易得到:对于任意割,实际流过去的量(净流量),不可能超过这个割原本的物理容量。这是我们的第二个引理。
Defination - Cut Lemma 2对于任意流 和任意割 :
那既然总流量不能超过任意一个割的容量,那它肯定也不能超过容量最小的那个割(最小割)。
Ford-Fulkerson 算法结束时,意味着在残存网络 中,已经找不到从 到 的路了。
此时,我们来构造一个特殊的割 :
- 集合 :在残存网络 中,从 出发能走到的所有节点。
- 集合 :在残存网络 中,从 出发走不到的所有节点。( 肯定在这里,因为如果能走到 ,算法就不该结束)
在这个特殊割 上:
- 对于所有 的正向边 :在残存网络里断了(不能走,因为能走的话会归到 里)。这意味着 。。 所有正向边都满载了!
- 对于所有 的反向边 :在残存网络里也没有边(不能倒着流回来,否则 就在 里了)。这意味着 。 所有反向边都是空的!
在这个特殊的割上:
所以,当 Ford-Fulkerson 结束时,我们找到了一个流和一个割,它们的数值相等。
因为割的引理2告诉我们,流 容量:对于任意割,实际流过去的量(净流量),不可能超过这个割原本的物理容量。即 。
既然在这个点上流碰到了割的天花板,流不可能更大了(这就是最大流),割也不可能更小了(这就是最小割)。
所以我们可以得出一个结论:一个网络的最大流量,等于该网络最小割的容量。
我们将这个过程用数学语言写出来,就成为了 最大流最小割定理 (Max-Flow Min-Cut Theorem)。
Defination - Max-Flow Min-Cut Theorem设 是流网络 中的一个流,源点为 ,汇点为 。 以下三个条件等价:
- 是 的一个最大流
- 残存网络 中不存在增广路径
- 存在某个割 ,使得
其实这三个条件就是 Ford-Fulkerson 方法结束时的情况。
我们通过一个例子去验证这个结论对不对,下面是一个流网络执行 Ford-Fulkerson 方法到最后一步时的流网络图 。
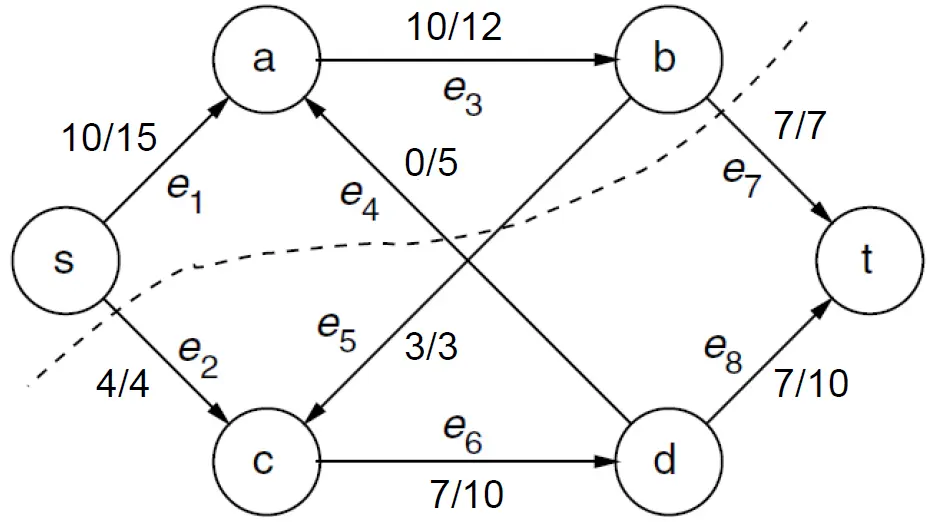
我们来验证它是否是最小割:
-
我们将其转换为残存网络:
10 (<)———> a <——————————————> b| / ↖ 2 (>) ↗ ↖ 75 | ↙ 10 \ / \s 5 (↖) \ / 3 (↗) t↖ / \ ↗ 3 (↗)4 \ 7 (<) 7 (↙) ↙c <——————————————> d3 (>)边 流 10 5 2 10 4 3 3 5 7 3 7 7 -
我们构建特殊的割:, 。
-
计算特殊割的残存容量,它是原图中所有 到 边的容量:
-
比较当前流的值是否等于割的容量:。所以当前割是最小割,当前流是最大流。
并且此时我们发现,割的净流量 , 的边都是满的, 都是空的。
Edmonds-Karp 算法
Edmonds-Karp 算法是 Ford-Fulkerson 方法最著名、最常用的具体实现。
在通用的 Ford-Fulkerson 方法中,我们说“找一条增广路径”。但是没说怎么找。 如果运气不好,这会导致灾难性的后果。
想象一个图:
- (容量 1,000,000)
- (容量 1,000,000)
- (容量 1,000,000)
- (容量 1,000,000)
- 中间有一条双向管道 (容量 1)
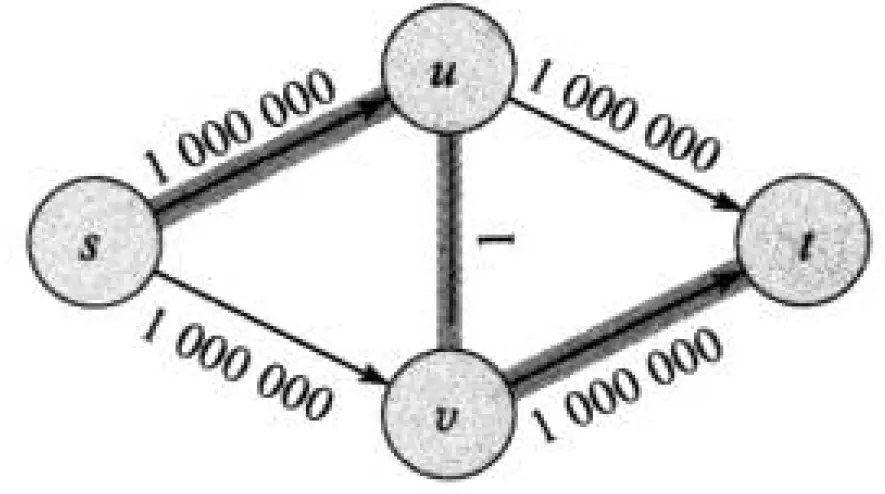
DFS (深度优先) 选路:
- 如果算法先选了 (利用了中间那条细管子),流量增加了 1。
- 下一步,算法发现了反向边,选了 (把中间那 1 单位流推回去),流量又增加了 1。
- 就这样, 的流推过去、推回来……每次总流量只 +1。
- 要达到 2,000,000 的最大流,电脑要循环 200 万次!
而 Edmonds-Karp 算法则是不要乱选路。永远只选“边数最少”的那条路。
在这个例子中,Edmonds-Karp 会直接看到 (2条边) 和 (2条边),两步搞定,瞬间结束。
此外,如果边的容量是无理数(比如 ),Ford-Fulkerson 可能永远运行下去,而且流的值可能收敛到一个不是最大流的值。
Edmonds-Karp 算法的思路很简单,每次选择最短的增广路径(边数最少的路径)。即:用 BFS 而不是 DFS 来寻找增广路径。
注意:这里的“短”不是指权值(容量)小,而是指 边的数量最少 ( 的长度是 3)。即把所有边的权重都视为 1 时的最短路。
下面我们通过一个例子来看看 Edmonds-Karp 算法的过程。
若存在一个初始网络 :
10┌───────────▶ v₁ ─────────┐│ │ │ 10│ │ 4 ││ ▼ ▼s v₃ ───────▶ t│ ▲ 10 ▲│ │ 2 ││ │ │ 10└───────────▶ v₂ ─────────┘ 10-
初始状态,所有边的流量初始化为 0:当前流 。它的残存网络和原图一样。
-
第 1 轮:BFS 找最短路径。BFS 从 开始:
- 层 0:
- 层 1:
- 层 2: ← 找到
最短路径(之一):
路径长度:2 条边
瓶颈容量:
当前流量:,图 :
10/10┌───────────▶ v₁ ─────────┐│ │ │ 10/10│ │ 0/4 ││ ▼ ▼s v₃ ───────▶ t│ ▲ 0/10 ▲│ │ 0/2 ││ │ │ 0/10└───────────▶ v₂ ─────────┘0/10残存图 :
10┌───────────── v₁ <────────┐│ │ │ 10│ │ 4 │▼ ▼ |s v₃ ───────▶ t│ ▲ 10 ▲│ │ 2 ││ │ │ 10└───────────▶ v₂ ─────────┘10 -
第 2 轮:BFS 找最短路径。BFS 从 开始:
- 层 0:
- 层 1: ( 的正向边没了)
- 层 2: ← 找到
最短路径:
瓶颈容量:
当前流量:
图 :
10/10┌───────────▶ v₁ ─────────┐│ │ │ 10/10│ │ 0/4 ││ ▼ ▼s v₃ ───────▶ t│ ▲ 0/10 ▲│ │ 0/2 ││ │ │ 10/10└───────────▶ v₂ ─────────┘10/10残存图 :
10┌───────────── v₁ <────────┐│ │ │ 10│ │ 4 │▼ ▼ |s v₃ ───────▶ t▲ ▲ 10 |│ │ 2 ││ │ │ 10└───────────── v₂ <────────┘10 -
第 3 轮:继续 BFS:
- 层 0:
- 层 1: {} (, 的正向边都没了)
无法到达 t,算法终止!
当前流量即最大流:
图 :
10/10┌───────────▶ v₁ ─────────┐│ │ │ 10/10│ │ 0/4 ││ ▼ ▼s v₃ ───────▶ t│ ▲ 0/10 ▲│ │ 0/2 ││ │ │ 10/10└───────────▶ v₂ ─────────┘10/10残存图 :
10┌───────────── v₁ <────────┐│ │ │ 10│ │ 4 │▼ ▼ |s v₃ ───────▶ t▲ ▲ 10 |│ │ 2 ││ │ │ 10└───────────── v₂ <────────┘10
为什么用 BFS 就能保证计算的复杂度下降呢?我们来进行复杂度的分析。
我们知道每次 BFS 我们都是选择条数最小的边,那么可以推出:
Defination - Edmonds-Karp Lemma 1设 表示在残存网络 中从 到 的最短路径长度(边数)。
在 Edmonds-Karp 算法执行过程中,对于所有顶点 :
我们可以理解其中的物理直觉:
-
每次我们在残存网络里用 BFS 找到一条最短路,并且把它填满(推流推到瓶颈容量),这条路径上至少有一条边(瓶颈边)会 满载。
-
满载意味着 断路:满载的边会从残存网络里消失(正向容量变0)。
-
这条边如果想以后再次在残存网络里出现,必须有流从反方向推回来。反向推流意味着我们通过反向边走了回头路,这势必会导致路径变得更长。
随着算法进行,从 到 的最短路径的长度(边数)只会越来越长,或者是保持不变,绝不会变短。
因为距离有上限(最多 个点),边数也有限,所以算法不可能无限循环下去,必然会在有限步内停止。
我们可以假设边 在某次增广中成为瓶颈:这条边这条边饱和后消失。要让它再次出现,必须有某次增广使用了反向边 。
由于最短距离单调不减:每次 成为瓶颈后再次成为瓶颈, 至少增加 2。
由于 ,所以 最多成为瓶颈 次。
这样我们得到了第二个引理:
Defination - Edmonds-Karp Lemma 2在整个算法过程中,每条边 最多成为增广路径的瓶颈边 次。
此时我们就可以计算其复杂度了,因为:
- 每次增广至少有一条边成为瓶颈。
- 每条边最多成为瓶颈 次。
- 总共有 条边。
因此:总增广次数 =
每次增广的过程中,BFS 找路径:,更新流量:。
总复杂度:
这个复杂度与容量的大小无关!不管容量是 1 还是 100 亿,只要图的结构(点和边)不变,它的运行时间上限就是固定的。所以该算法被称为“多项式时间”算法。
后记
我们从流网络的基本概念出发:一个有向图,有源点 、汇点 ,每条边有容量限制。流必须满足两个约束——容量限制(不能超载)和流量守恒(除了源汇,流入等于流出)。
为了找最大流,我们引入了残存网络 :它告诉我们”还能怎么调整”。残存网络包含两种边——正向边表示还能增加多少流量,反向边表示可以撤销多少已有流量。在残存网络中从 到 的路径称为增广路径,沿着它我们可以增加总流量。增广操作 的本质就是:新流量 = 原流量 + 增加量 - 撤销量。
接着我们学习了割的概念:把顶点分成包含 的 和包含 的 两部分,割的容量是所有从 到 的边的容量之和。最大流最小割定理揭示了一个深刻的对偶性:最大流的值恰好等于最小割的容量。更重要的是,它给出了最优性的判定条件——当且仅当残存网络中不存在增广路径时,当前流是最大流。
最后,Edmonds-Karp 算法通过一个简单的改进——用 BFS 寻找最短增广路径——将复杂度从依赖于流值的 降到了真正多项式时间的 。其核心洞察是:BFS 保证最短路径距离单调不减,从而限制了每条边成为瓶颈的次数。

