
前言
单源最短路径(single-source shortest-paths problem) 是指在一个加权有向图或加权无向图中,从给定源节点到图中其他所有节点的最短路径。这个问题的目标是找到一条路径,使得从源节点到达其他节点的路径长度最短。
路径的长度是通过节点之间的边上的权重来定义的。每条边都有一个非负的权重值,表示从一个节点到另一个节点的距离或代价。单源最短路径算法旨在确定从源节点到所有其他节点的最短路径,并给出路径的长度。
常用的单源最短路径算法包括Bellman-Ford算法和Dijkstra算法。
Bellman-Ford算法
Bellman-Ford算法解决的是一般情况下单源最短路径问题,边的权重可以为负值,给定源点为s的有向带权图 G =(V, E)和权重函数 w: E->R,Bellman-Ford算法返回一个布尔值,该布尔值表明是否存在一个从源点可达的负权重的环路。若存在这样一个环路(有负权重的环路),则算法提示不存在解决方案。若不存在这样一个环路,则算法给出最短路径和它们的权重。
Bellman-Ford算法的基本思想是,从源节点(s)开始,对所有其他节点进行V-1次松弛操作(通过尝试更新节点之间的距离估计值来改善当前的路径长度),其中V是图中节点的数量。每次松弛操作都会尝试通过当前节点更新到其他节点的距离估计值,直到所有节点的最短路径长度被确定。如果在V-1次松弛操作后仍然存在可以改进的路径,则说明存在负权回路,即图中存在无限负权的环路。
在介绍Bellman-Ford算法之前,我们先介绍几个工具函数:
- INITIALIZE-SINGLE-SOURCE(G, s)函数初始化了整个单源最短路,将所有的节点的d设为∞,π设为NIL。
- RELAX(u, v, w)函数为松弛操作,输入为节点u、节点v以及u到v的边的权重w。通过这个松弛操作,我们可以不断更新节点的距离估计值和前驱节点,以便找到最短路径。
INITIALIZE-SINGLE-SOURCE(G, s) for each vertex v ∈ G.V v.d = ∞ v.π = NIL s.d = 0松弛操作:
RELAX(u, v, w) if v.d > u.d + w(u, v) v.d = u.d + w(u, v) v.π = u-
首先,我们检查通过节点u到达节点v的路径是否比节点v当前的最短路径更短(即节点v.d > u.d + w(u, v))。
-
如果通过节点u到达节点v的路径长度更短,那么我们将节点v的距离估计值v.d更新为通过节点u到达节点v的路径长度(即v.d = u.d + w(u, v))。
-
同时,我们将节点u标记为节点v的前驱节点(即v.π = u),表示通过节点u可以达到节点v,并构成最短路径中节点v的前一个节点。
用两个例子来解释松弛操作:
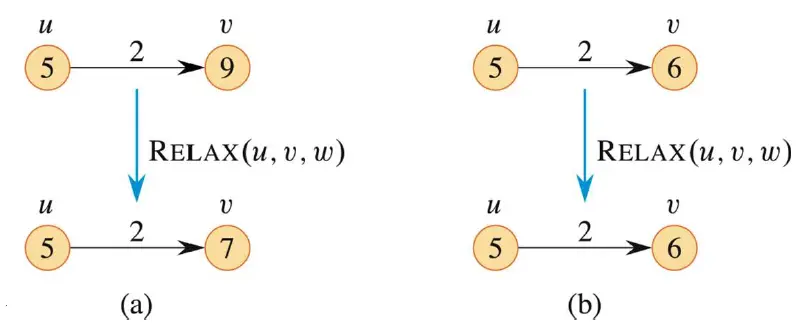
对权重w(u,v)=2的边(u,v)进行的松驰操作。对每个结点的最短路径估计写在结点里面。
- (a)因为在松驰操作前有v.d > u.d + w(u,v) 因而v.d的值减小。
- (b)在对边进行松弛操作前有v.d < u.d + w(u,v) ,因此,松驰步骤维持v.d的取值不变。
过程 BELLMAN-FORD 通过不断松弛边,逐步减少从源点s到每个顶点v∈V的最短路估计 v.d,循环查找|G.V| - 1次,直到 v.d = δ(s,v),该算法返回 TRUE 当且仅当不存在一个从源点可达的负权重的环路。过程 BELLMAN-FORD的伪代码如下:
BELLMAN-FORD(G, w, s) INITIALIZE-SINGLE-SOURCE(G, s) for i = 1 to |G.V| − 1 for each edge (u, v) ∈ G.E RELAX(u, v, w) for each edge (u, v) = G.E if v.d > u.d + w(u, v) return FALSE return TRUE在算法的最后,通过迭代所有图中的边(for each edge (u, v) ∈ G.E),我们检查是否存在一条边,它的终点节点v的最短路径估计值(v.d)可以通过起点节点u的最短路径估计值(u.d)加上边的权重(w(u, v))而得到。
-
对于每一条边 (u, v) ∈ G.E,我们检查 v.d 是否大于 u.d 加上从 u 到 v 的边的权重 w(u, v)。
-
如果存在一条边 (u, v) 满足 v.d > u.d + w(u, v),那么意味着存在一条路径从源节点 s 经过节点 u 到达节点 v,路径的长度比当前的最短路径估计值更短。
-
这种情况下,返回 FALSE 表示图中存在负权回路(negative-weight cycle),即存在一个环路,使得沿着这个环路的路径可以无限次地减小路径的长度。
-
如果算法返回 TRUE,表示图中不存在负权回路,并且算法能够确定每个节点的最短路径。这意味着可以从源节点 s 到达图中的任何节点,并且返回的最短路径估计值是准确的。
我们通过一个例子来解释这个过程:
如果设 z 为源点,按照如下顺序 (t, x), (t, y), (t, z), (x, t), (y, x), (y, z), (z, x), (z, s), (s, t), (s, y) 松弛边的话,如下图,找出每个节点的d值(最短路长)和π值(前驱节点)的表格。
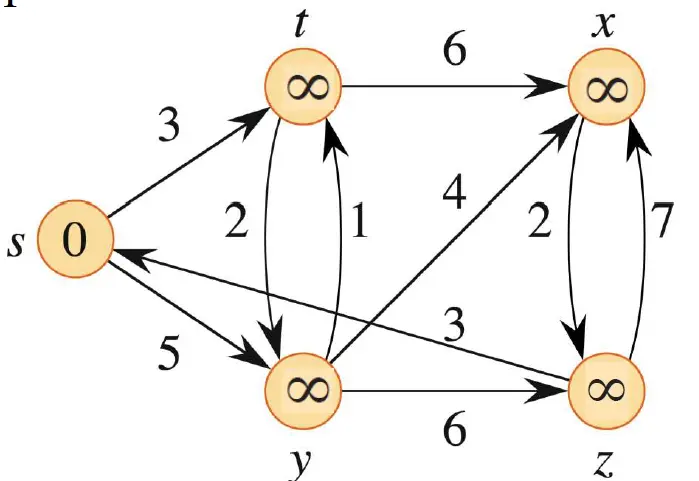
-
首先,通过
INITIALIZE-SINGLE-SOURCE操作,将所有顶点的d值设置为∞,π值设置为NIL。设置源点z.d = 0. -
第一次循环:从z出发,按照顺序遍历这些节点,此时根据 (z, x), (z, s), (s, t), (s, y) ,我们可以把x和s的值设置:x.d = 7, x.π = z; s.d = 2, s.π = z; 在设置好s后,还有t.d = 8, t.π = s; y.d = 9, y.π = s。
-
第二次循环:根据顺序有 (t, x), (t, y), (t, z), (x, t), (y, x), (y, z), (z, x), (z, s), (s, t), (s, y) ,通过松弛这些边得到:t.d = 5, t.π = x; x.d = 6, x.π = y。
-
第三次循环中,在松弛边 (x, t) 时,因为上一步x的d值改了,这里也会一并改动。t.d = 4, t.π = x。
-
第四次循环,没有任何节点的最短路被改变。
-
在算法的最后一个步骤中,检查每一条边是否满足v.d ≤ u.d + w(u, v),我们发现对于每一条边都满足这个式子,故返回TRUE.
这个例子的d值表为:
| s | t | x | y | z |
|---|---|---|---|---|
| ∞ | ∞ | ∞ | ∞ | 0 |
| 2 | 8 | 7 | 9 | 0 |
| 2 | 5 | 6 | 9 | 0 |
| 2 | 4 | 6 | 9 | 0 |
| 2 | 4 | 6 | 9 | 0 |
π表为:
| s | t | x | y | z |
|---|---|---|---|---|
| NIL | NIL | NIL | NIL | NIL |
| z | s | z | s | NIL |
| z | x | y | s | NIL |
| z | x | y | s | NIL |
| z | x | y | s | NIL |
返回TRUE,因为每条边都满足:v.d ≤ u.d + w(u, v)。
Dijkstra算法
Dijkstra的算法解决了加权有向图上的单源最短路径问题,但它要求所有边的权重是非负的。它有如下特点:
- 基本上可以看成是BFS的加权版本。
- 不使用FIFO队列,而是使用优先队列。
- 关键字是最短路径权重(v,d)。
- 当一层搜索第一次到达某个顶点时,一个新的搜索从这个顶点发出。
- 搜索到达相邻顶点所需的时间等于边的权重。
Dijkstra算法维持一个顶点集合 S,表示从s可达的最终最短距离已经确定的顶点的集合。Dijkstra算法不断从 V -S 中选择具有最小路径估计的顶点 u,然后将u加入 S,并松驰所有从u发出的边。即节点u出队时进入S中。
过程 Dijkstra 使用以顶点的 d 值为关键字的优先队列,伪代码如下:
DIJKSTRA(G, w, s) INITIALIZE-SINGLE-SOURCE(G, s) S = Ø Q = Ø for each vertex u ∈ G.V INSERT(Q, u) while Q ≠ Ø u = EXTRACT-MIN(Q) S = S ∪ {u} for each vertex v in G.Adj[u] RELAX(u, v, w) if the call of RELAX decreased v.d DECREASE-KEY(Q, v, v.d)我们同样通过一个例子来理解这个算法,原理和BFS非常像:
如下图,若我们以s为源点,找到所有顶点在算法过程中的d值和π值,以及集合S表示最短路径。

-
首先,通过
INITIALIZE-SINGLE-SOURCE操作,将所有顶点的d值设置为∞,π值设置为NIL,S和Q为Ø。设置源点s.d = 0,s入队. -
接下来,s出队,t和y进入优先队列Q,更新t和y的值:t.d = 3, t.π = s;y.d = 5,y.π = s;此时最短路集合S = s。
-
t出队,它可以更新x的值,并将x入队:x.d = 9, x.π = t;此时最短路集合S = s, t。
-
y出队,它可以更新z的值,并将z入队:z.d = 11, z.π = y;此时最短路集合S = s, t, y。
-
x出队,无事发生,此时最短路集合S = s, t, y, x;
-
z出队,无事发生,此时最短路集合S = s, t, y, x, z;
d值表:
| s | t | x | y | z |
|---|---|---|---|---|
| 0 | ∞ | ∞ | ∞ | ∞ |
| 0 | 3 | ∞ | 5 | ∞ |
| 0 | 3 | 9 | 5 | 11 |
| 0 | 3 | 9 | 5 | 11 |
| 0 | 3 | 9 | 5 | 11 |
π值表:
| s | t | x | y | z |
|---|---|---|---|---|
| NIL | NIL | NIL | NIL | NIL |
| NIL | s | NIL | s | NIL |
| NIL | s | t | s | NIL |
| NIL | s | t | s | y |
| NIL | s | t | s | y |
S:s, t, y, x, z
后记
单源最短路径问题是图论中的经典问题,对于很多实际应用具有重要意义。Bellman-Ford算法和Dijkstra算法是解决单源最短路径问题的两种常用算法,它们在不同的情况下展现出优势和适用性。
Bellman-Ford算法适用于一般情况下的单源最短路径问题,可以处理边权重为负值的情况。它通过多次松弛操作来逐步确定最短路径,并能够检测是否存在负权回路。然而,由于其时间复杂度为O(V*E),在图较大或边数较多的情况下,效率可能较低。
Dijkstra算法适用于边权重非负的加权有向图的单源最短路径问题。它通过维护一个顶点集合和优先队列来选择具有最小路径估计的顶点,并进行松弛操作。相比于Bellman-Ford算法,Dijkstra算法具有更高的效率,其时间复杂度为O((V+E)logV)。然而,由于其要求边权重非负,因此无法处理负权边的情况。
在实际应用中,我们需要根据具体问题的要求和图的特征选择合适的算法。如果图中存在负权回路或需要处理负权边,可以选择Bellman-Ford算法。而对于边权重非负的情况,Dijkstra算法是一个较好的选择。同时,还可以根据实际情况考虑其他算法或优化策略,以提高计算效率和解决问题的准确性。

